Точки разрыва функции и их классификация

Точки разрыва функции классифицируются следующим образом:

Определение 3. Точка 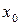называется точкой разрыва первого рода функции 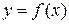, если в этой точке существуют конечные пределы 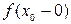и 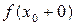, но они не равны между собой: . Величина называется скачком функции 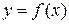в точке .

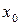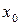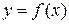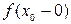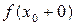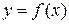Определение 4. Точка называется точкой устранимого разрыва функции , если в этой точке существуют конечные пределы и , они равны между собой: , но сама функция не определена в точке 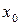или определена, но .

Определение 5. Точка 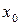называется точкой разрыва второго рода функции 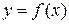, если в этой точке хотя бы один из односторонних пределов ( 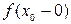или 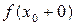) не существует или равен бесконечности.

Пример 3. Найти точки разрыва следующих функций и определить их тип:

а)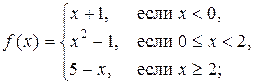

б)

Решение:

а) функция 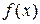определена и непрерывна на интервалах 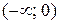, 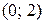и , так как на каждом из этих интервалов она задана непрерывными элементарными функциями. Следовательно, точками разрыва данной функции могут быть только те точки, в которых функция меняет свое аналитическое задание, т.е. точк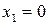и и . Найдем односторонние пределы функции в точке :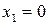

, .

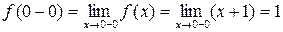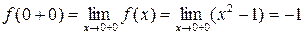Так как односторонние пределы существуют и конечны, но не равны между собой, то точка 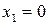является точкой разрыва первого рода. Скачок функции: .

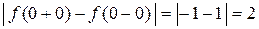Для точки находим:

,

, .

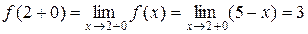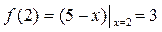Таким образом, имеем: 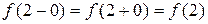. Следовательно, в точке наша функция является непрерывной.

График данной функции изображен на рисунке:

б) в точке функция меняет свое аналитическое задание, следовательно, в этой точке возможен разрыв. Найдем односторонние пределы:

,

, .

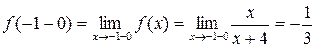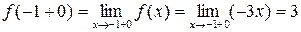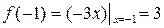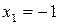Так как , то точка является точкой разрыва первого рода. Скачок функции: .

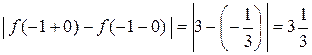В точке 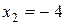функция не определена, значит, точка является точкой разрыва. Определим ее тип:

, .

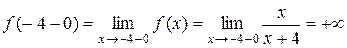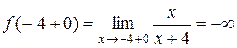Следовательно, в точке функция имеет разрыв второго рода.

Date: 2016-07-25; view: 356; Нарушение авторских прав