
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Элементы скалярного поля
|
|
Производная скалярного поля  по направлению вектора
по направлению вектора
|
 z
z
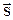

 M0
M0
M β
α
0 у
x Рис. 3
Пример 6. Найти скорость изменения скалярного поля  в точке
в точке  в направлении от этой точки к точке
в направлении от этой точки к точке  .
.
Решение. Скорость изменения скалярного поля в направлении вектора  в точке
в точке  определяют по формуле
определяют по формуле
 .
.
В задаче  ,
,  ,
,
 .
.
 ,
,
 ,
,
 .
.
Подставим все найденные величины в первую формулу:
 .
.
Ответ: В заданном направлении данное скалярное поле убывает со скоростью  .
.
Градиент скалярного поля 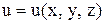 – вектор
– вектор

 .
.
Очевидно,
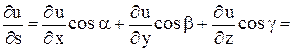
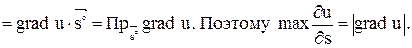

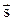

|

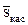
Рис. 7
Пример 7. Найти величину градиента скалярного поля 
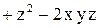 в точке
в точке 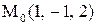 .
.
Решение.
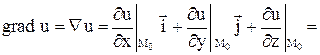
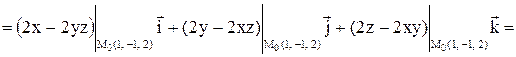
 .
.
 .
.
Ответ:  .
.
Задача 4. Найти производную функции  в точке
в точке  в направлении от этой точки к точке
в направлении от этой точки к точке  .
.
Решение. Напишем формулу производной функции по направлению вектора  .
.
 , где
, где  - орт направления вектора
- орт направления вектора  .
.
Сначала найдем вектор  , в направлении которого будем искать производную.
, в направлении которого будем искать производную.  =
=  . Найдем длину
. Найдем длину  .
.  . Направляющие косинусы вектора
. Направляющие косинусы вектора  совпадают с координатами орта
совпадают с координатами орта  , поэтому
, поэтому 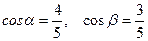 .
.
Теперь найдем частные производные функции 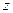 .
.

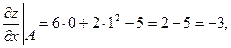
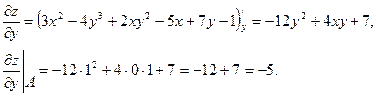
Все найденные значения подставляем в формулу производной по направлению.
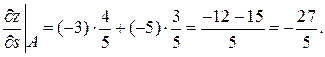
Вывод. Функция 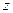 убывает по направлению вектора
убывает по направлению вектора  , так как полученная производная меньше нуля.
, так как полученная производная меньше нуля.
Ответ: 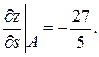
Контрольные варианты к задаче 4.
Найти производную функции:
| 1. |  в точке (3; 1) в направлении от этой точки к точке (6; 5). в точке (3; 1) в направлении от этой точки к точке (6; 5).
|
| 2. | 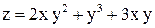 в точке (4; 1) в направлении от этой точки к точке (5; 1). в точке (4; 1) в направлении от этой точки к точке (5; 1).
|
| 3. |  в точке (2; 1) в направлении от этой точки к началу координат. в точке (2; 1) в направлении от этой точки к началу координат.
|
| 4. |  в точке (3; 1) в направлении от этой точки к точке (6; 5). в точке (3; 1) в направлении от этой точки к точке (6; 5).
|
| 5. |  в точке (1; 1) в направлении от этой точки к точке (2; 2). в точке (1; 1) в направлении от этой точки к точке (2; 2).
|
| 6. |  в точке (1; 2) в направлении от этой точки к точке (1; 1). в точке (1; 2) в направлении от этой точки к точке (1; 1).
|
| 7. |  в точке (5; 1) в направлении от этой точки к точке (9; 4). в точке (5; 1) в направлении от этой точки к точке (9; 4).
|
| 8. |  в точке (1; 2) в направлении от этой точки к точке (1; 1). в точке (1; 2) в направлении от этой точки к точке (1; 1).
|
| 9. |  в точке (2; 1) в направлении от этой точки к началу координат. в точке (2; 1) в направлении от этой точки к началу координат.
|
| 10. | 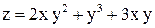 в точке (4; 1) в направлении от этой точки к точке (5; 1). в точке (4; 1) в направлении от этой точки к точке (5; 1).
|
| 11. |  в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о. в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о.
|
| 12. |  в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о. в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о.
|
| 13. |  в точке (1; 1) в направлении биссектрисы 1-го координатного угла. в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
|
| 14. |  в точке (1; 2) в направлении, составляющем с осью OX угол в 60о. в точке (1; 2) в направлении, составляющем с осью OX угол в 60о.
|
| 15. |  в точке (1; 1) по направлению вектора в точке (1; 1) по направлению вектора  . .
|
| 16. |  в начале координат в направлении луча, образующего угол в 30о с осью OX. в начале координат в направлении луча, образующего угол в 30о с осью OX.
|
| 17. |  в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ. в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ.
|
| 18. | 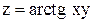 в точке (1; 1) в направлении биссектрисы 1-го координатного угла. в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
|
| 19. |  в точке (3; 1) по направлению вектора в точке (3; 1) по направлению вектора  . .
|
| 20. |  в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ. в точке (1; 1) в направлении луча, образующего угол в 60о с осью ОХ.
|
| 21. |  в начале координат в направлении луча, образующего угол в 30о с осью OX. в начале координат в направлении луча, образующего угол в 30о с осью OX.
|
| 22. |  в точке (1; 3) по направлению вектора в точке (1; 3) по направлению вектора  . .
|
| 23. |  в точке (1; 2) в направлении, составляющем с осью OX угол в 60о. в точке (1; 2) в направлении, составляющем с осью OX угол в 60о.
|
| 24. |  в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о. в точке (1; 2) в направлении вектора, образующего с осью OX угол в 45о.
|
| 25. |  в точке (3; 1) по направлению вектора в точке (3; 1) по направлению вектора  . .
|
| 26. |  в точке (1; 1) в направлении биссектрисы 1-го координатного угла. в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
|
| 27. |  в точке (1; 3) по направлению вектора в точке (1; 3) по направлению вектора  . .
|
| 28. |  в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о. в точке (1; 1) в направлении, образующем углы α = 30о, β = 60о.
|
| 29. | 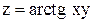 в точке (1; 1) в направлении биссектрисы 1-го координатного угла. в точке (1; 1) в направлении биссектрисы 1-го координатного угла.
|
| 30. |  в точке (5; 1) в направлении от этой точки к точке (9; 4). в точке (5; 1) в направлении от этой точки к точке (9; 4).
|
Date: 2016-07-18; view: 829; Нарушение авторских прав
 (рис.3).
определяется так:
(рис.3).
определяется так:  – это скорость изменения скалярного поля
– это скорость изменения скалярного поля 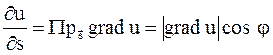 (рис. 7).
(рис. 7).