
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В замкнутой области D
|
|
Правило. Чтобы найти М – наибольшее и m – наименьшее значения функции 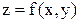 в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения
в замкнутой области D, находят критические точки этой функции. Если эти точки принадлежат области D, то в них следует вычислить значения 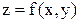 . Затем, используя уравнения границы L области D, нужно найти критические точки
. Затем, используя уравнения границы L области D, нужно найти критические точки 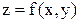 , принадлежащие L, вычислить в них значения
, принадлежащие L, вычислить в них значения 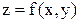 . Вычислить значения
. Вычислить значения 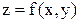 на концах L. Осталось из всех найденных значений данной функции
на концах L. Осталось из всех найденных значений данной функции 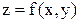 выбрать самое большое М и самое малое m.
выбрать самое большое М и самое малое m.
Задача 3. Найти наибольшее М и наименьшее m значения функции 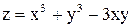 в прямоугольнике
в прямоугольнике  .
.
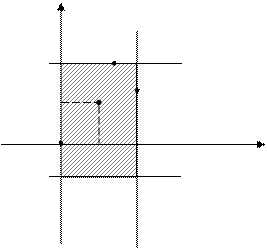
Решение. Найдем критические точки функции z, которые принадлежат заданной области (рис. 2).
|
B(0, 2)  C(2, 2)
C(2, 2)
|
1 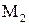
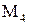
x=2
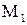 1 2 x
1 2 x
у=-1
A(0, -1) D(2, -1)
Рис. 2
Таким образом, решений у системы два: 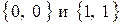 . Первому решению соответствует точка
. Первому решению соответствует точка  , которая принадлежит границе области. Второму решению соответствует критическая точка
, которая принадлежит границе области. Второму решению соответствует критическая точка 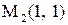 , которая принадлежит области, поэтому вычислим значения функции в ней:
, которая принадлежит области, поэтому вычислим значения функции в ней: 
 .
.
Исследуем функцию z на границе области (прямоугольник ABCD), которая состоит из четырех звеньев:
1. АВ:  .
.
Получили задачу на экстремум для функции одной переменной. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке  .
.  . Получаем критическую точку
. Получаем критическую точку 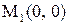 , вычислим функцию в этой точке:
, вычислим функцию в этой точке:  .
.
2. ВС:  . Найдем производную этой функции:
. Найдем производную этой функции:  , корень уравнения
, корень уравнения 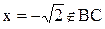 , поэтому критическая точка
, поэтому критическая точка 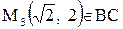 . Вычислим значение функции в ней:
. Вычислим значение функции в ней:  .
.
 .
.
3. СD:  . Найдем
. Найдем 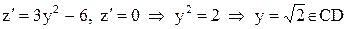 , а
, а  . Поэтому критическая точка
. Поэтому критическая точка  . Вычислим в ней значение функции:
. Вычислим в ней значение функции:


 .
. 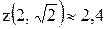 .
.
4. AD:  . Найдем производную этой функции:
. Найдем производную этой функции:  , действительных корней не имеет.
, действительных корней не имеет.
5. Осталось вычислить значения функции 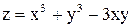 на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника
на концах каждого из отрезков, являющихся сторонами прямоугольника: АВ, BC, CD, AD, т. Е. в вершинах прямоугольника  .
.
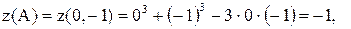
 ,
,

 ,
,
 ,
,  ,
,
 ,
,  .
.
Сравнив все подчеркнутые значения функции z (только они представляют интерес), делаем вывод: наибольшее значение z достигает в вершине прямоугольника D, т. Е. 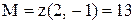 , а наименьшее – в двух точках: во внутренней точке области
, а наименьшее – в двух точках: во внутренней точке области  и в вершине.
и в вершине.
Контрольные варианты к задаче 3.
Найти наибольшее и наименьшее значения функции:
| 1. |  в треугольнике со сторонами в треугольнике со сторонами 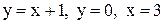 . .
|
| 2. |  в треугольнике со сторонами в треугольнике со сторонами  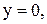  . .
|
| 3. |  в замкнутой области, ограниченной в замкнутой области, ограниченной  и осью и осью  . .
|
| 4. | 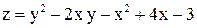 в треугольнике со сторонами в треугольнике со сторонами 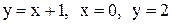 . .
|
| 5. |  в треугольнике со сторонами в треугольнике со сторонами  
|
| 6. |  в замкнутой области, ограниченной в замкнутой области, ограниченной  и осью и осью  . .
|
| 7. |  в квадрате в квадрате 
|
| 8. |  в квадрате в квадрате 
|
| 9. |  в замкнутой области, ограниченной линиями в замкнутой области, ограниченной линиями  и и 
|
| 10. |  в области, ограниченной прямыми в области, ограниченной прямыми 
|
| 11. |  в области, ограниченной прямыми в области, ограниченной прямыми 
|
| 12. |  в прямоугольнике, ограниченном прямыми в прямоугольнике, ограниченном прямыми 

|
| 13. |  в треугольнике со сторонами в треугольнике со сторонами 
|
| 14. |  в треугольнике со сторонами в треугольнике со сторонами 
|
| 15. | 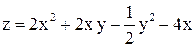 в треугольнике со сторонами в треугольнике со сторонами 
|
| 16. |  в квадрате, ограниченном прямыми в квадрате, ограниченном прямыми   
|
| 17. |  в треугольнике со сторонами в треугольнике со сторонами 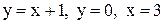 . .
|
| 18. |  в треугольнике со сторонами в треугольнике со сторонами  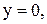  . .
|
| 19. |  в замкнутой области, ограниченной в замкнутой области, ограниченной  и осью и осью  . .
|
| 20. | 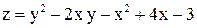 в треугольнике со сторонами в треугольнике со сторонами 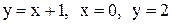 . .
|
| 21. |  в треугольнике со сторонами в треугольнике со сторонами  
|
| 22. |  в замкнутой области, ограниченной в замкнутой области, ограниченной  и осью и осью  . .
|
| 23. |  в квадрате в квадрате 
|
| 24. |  в квадрате в квадрате 
|
| 25. |  в замкнутой области, ограниченной линиями в замкнутой области, ограниченной линиями  и и 
|
| 26. |  в области, ограниченной прямыми в области, ограниченной прямыми 
|
| 27. |  в области, ограниченной прямыми в области, ограниченной прямыми 
|
| 28. |  в прямоугольнике, ограниченном прямыми в прямоугольнике, ограниченном прямыми 

|
| 29. |  в треугольнике со сторонами в треугольнике со сторонами 
|
| 30. |  в треугольнике со сторонами в треугольнике со сторонами 
|
Date: 2016-07-18; view: 367; Нарушение авторских прав

 подставим
подставим 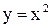 во второе уравнение:
во второе уравнение:  , т. е.
, т. е. 
