
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие и основные свойства функции
|
|
Постоянной величиной называется величина, сохраняющая одно и то же значение. Например, отношение длины окружности к ее диаметру есть постоянная величина, равная числу  .
.
Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.
Переменной называется величина, которая может принимать различные числовые значения. Например, при равномерном движении S=vt, где путь S и время t – переменные величины, а v – параметр.
Перейдем к понятию функции.
ОПРЕДЕЛЕНИЕ. Если каждому элементу x множества X (x  X) ставится в соответствие вполне определенный элемент y множества Y (y
X) ставится в соответствие вполне определенный элемент y множества Y (y  Y), то говорят, что на множестве X задана функция y=f(x).
Y), то говорят, что на множестве X задана функция y=f(x).
При этом x называется независимой переменной (или аргументом), y – зависимой переменной, а буква f обозначает закон соответствия.
Множество X называется областью определения (или существования) функции и обозначается  , а множество Y – областью значений функции и обозначается
, а множество Y – областью значений функции и обозначается  .
.
Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной x, т.е. множество таких значений x, при которых функция y=f(x) вообще имеет смысл.
Пусть  есть функция от независимой переменной x, определенной на множестве X с областью значений Y. Поставим(если это возможно) в соответствие каждому
есть функция от независимой переменной x, определенной на множестве X с областью значений Y. Поставим(если это возможно) в соответствие каждому 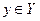 единственное значение
единственное значение  , при котором
, при котором  Тогда полученная функция
Тогда полученная функция  , определенная на множестве Y с областью значений X, называется обратной. Будем записывать обратную функцию в виде
, определенная на множестве Y с областью значений X, называется обратной. Будем записывать обратную функцию в виде  или, по аналогии с обозначением обратной величины,
или, по аналогии с обозначением обратной величины,  . Известно, что функция имеет обратную на промежутке (a;b) тогда и только тогда, когда она строго монотонна на этом промежутке (см. раздел 2.8).
. Известно, что функция имеет обратную на промежутке (a;b) тогда и только тогда, когда она строго монотонна на этом промежутке (см. раздел 2.8).
Среди функций выделяют основные элементарные функции, к ним относятся степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются э лементарными (подробнее см. раздел 2.9).
ПРИМЕР 1. Область определения функции y=  есть полуинтервал (-
есть полуинтервал (-  ; 10], так как 10- x
; 10], так как 10- x  0; если же переменная x обозначает, предположим, время, то при естественном дополнительном условии x
0; если же переменная x обозначает, предположим, время, то при естественном дополнительном условии x  0 областью определения функции будет отрезок [0; 10].
0 областью определения функции будет отрезок [0; 10].
Способы задания функций. Существует несколько способов задания функции.
а) Аналитический способ, если функция задана формулой вида y=f(x). Этот способ наиболее часто встречается на практике. Так, функция y =  , рассматриваемая выше, задана аналитически.
, рассматриваемая выше, задана аналитически.
Не следует путать функцию с ее аналитическим выражением. Так, например, одна функция y= 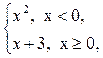
имеет два аналитических выражения  (при x <0) и x +3 (при x
(при x <0) и x +3 (при x 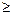 0).
0).
При этом различают функции, заданные явно, и функции, заданные неявно. Функция называется явной, если она задана формулой, в которой правая часть не содержит независимой переменной; например, функция 
Функция y аргумента x называется неявной, если она задана уравнением  ,не разрешенным относительно зависимой переменной. Например, функция y(
,не разрешенным относительно зависимой переменной. Например, функция y( ), заданная уравнением
), заданная уравнением  .
.
б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента x и соответствующие значения функции f(x), пример:
| x | ||||||
| f(x) |
в) Графический способ состоит в изображении графика функции – множества точек (x, y) плоскости, абсциссы которых есть значения аргумента x, а ординаты – соответствующие им значения функции y=f(x).
г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: f(x) = 1, если x – рационально; f(x) = 0, если x – иррационально.
РЕШЕНИЕ ЗАДАЧ
ПРИМЕР 1. Найти область определения функций:
1.  ; 2.
; 2.  .
.
Решение.
1. Область определения функции найдем из системы неравенств 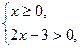 откуда
откуда  или
или  .
.
2. Область определения функции найдем из системы неравенств  откуда
откуда 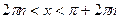 и
и  С помощью числовой оси находим, что
С помощью числовой оси находим, что  .
.
ПРИМЕР 2. Найти область значений функций:
1.  .
.
Решение.
Выразим x через y. Получим функцию 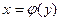 , заданную неявно квадратным уравнением
, заданную неявно квадратным уравнением  Область определения этой функции найдется из условия, что дискриминант
Область определения этой функции найдется из условия, что дискриминант
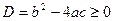 , т. е.
, т. е.  или
или  . Таким образом,
. Таким образом, 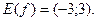 Отсюда также следует, что функция является ограниченной.
Отсюда также следует, что функция является ограниченной.
2.  .
.
Решение.
Преобразуем функцию

Отсюда видно, что область значений функции 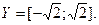
УПРАЖНЕНИЯ
Найти область определения функций:
2.1. 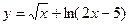 .
.
2.2. 
2.3. 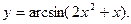
2.4. 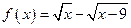
2.5. 
2.6. 
2.7. 
2.8. 
2.9. 
2.10. 
2.11. 
2.12. 
2.13. 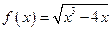
2.14. 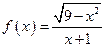
2.15. 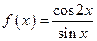
2.16. 
Найти область значений функций:
2.17. 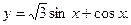
2.18. 
2.19. 
2.20. 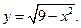
2.21. 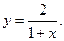
2.22. 
2.23. 
2.24. 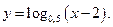
2.25. 
Ответы к упражнениям
2.1.  2.2.
2.2.  2.3.
2.3. 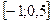 2.4.
2.4. 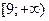 2.5.
2.5.  2.6.
2.6.  2.7. множество вещественных чисел 2.8.
2.7. множество вещественных чисел 2.8.  2.9.
2.9.  2.10.
2.10.  2.11.
2.11. 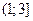 2.12.
2.12. 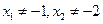 2.13.
2.13.  2.14.
2.14.  2.15.
2.15. 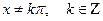 2.16.
2.16.  2.17.
2.17.  2.18.
2.18. 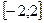 . 2.19.
. 2.19.  2.20.
2.20.  2.21.
2.21. 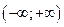 2.22.
2.22.  2.23.
2.23.  2.24.
2.24. 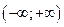 2.25.
2.25. 
Date: 2016-05-17; view: 498; Нарушение авторских прав