
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Выпуклость и вогнутость функции. Точки перегиба
|
|
Функция f(x), определенная и непрерывная на промежутке [ a, b ], называется выпуклой (вниз), если для любых точек  ,
, 
 [ a, b ] и числа
[ a, b ] и числа  , 0
, 0 

 1 выполняется неравенство
1 выполняется неравенство
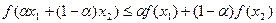 .
.
Функция f(x), определенная и непрерывная на промежутке [ a, b ], называется вогнутой (выпуклой вверх), если для любых точек  ,
, 
 [ a, b ] и числа
[ a, b ] и числа  , 0
, 0 

 1 выполняется неравенство
1 выполняется неравенство
 .
.
Приведенные определения имеют вполне определенный геометрический смысл. Выпуклая функция характеризуется тем, что все точки любой дуги ее графика лежат под соответствующей хордой или на ней (рис. 2.11). В случае вогнутой функции точки любой дуги графика лежат над хордой или на ней (рис.2.12).


Рис.2.11 Рис.2.12
Точку  (
( , f(
, f(  )) называют точкой перегиба функции f(x), если она отделяет участок кривой, где функция f(x) выпукла, от участка, где эта функция вогнута.
)) называют точкой перегиба функции f(x), если она отделяет участок кривой, где функция f(x) выпукла, от участка, где эта функция вогнута.
Достаточное условие выпуклости (вогнутости) функции. Если  для всех x
для всех x  [ a, b ], то функция f(x) выпукла на этом промежутке, если же
[ a, b ], то функция f(x) выпукла на этом промежутке, если же  для всех x
для всех x  [ a, b ], то функция f(x) вогнута на этом промежутке.
[ a, b ], то функция f(x) вогнута на этом промежутке.
Необходимое условие точки перегиба. Если функция f(x) дважды дифференцируемая в некоторой окрестности точки x 0, имеет в x 0 точку перегиба, то 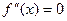 .
.
Достаточное условие точки перегиба. Если функция f(x) дважды дифференцируема в некоторой окрестности точки x 0 и  меняет знак при переходе через точку
меняет знак при переходе через точку  , то точка
, то точка  (
( , f(
, f(  )) является точкой перегиба функции f(x).
)) является точкой перегиба функции f(x).
Обратите внимание, что в достаточном условии точки перегиба нет требования существования второй производной в рассматриваемой точке  .
.
РЕШЕНИЕ ЗАДАЧ
Найдем промежутки выпуклости и вогнутости, точки перегиба следующих функций:
ПРИМЕР 1. f(x) =  ;
;
Решение. Находим производные:
 ;
;
 , откуда
, откуда  =0 при
=0 при  =
=  =1.5.
=1.5.
Из неравенств
 для -
для -  < x <1.5,
< x <1.5,
 для 1.5< x <+
для 1.5< x <+  следует, что на промежутке (-
следует, что на промежутке (-  ,1.5) функция f(x) вогнутая, а на промежутке (1.5,+
,1.5) функция f(x) вогнутая, а на промежутке (1.5,+  ) – выпуклая, точка
) – выпуклая, точка  (1.5,-7.5) – точка перегиба.
(1.5,-7.5) – точка перегиба.

ПРИМЕР 2. f(x) =  ;
;
Решение. Находим производные:
 ,
,
 , откуда
, откуда  при
при  = -2,
= -2,  =1.5.
=1.5.
Решая квадратичные неравенства, находим, что
 для -
для -  < x <-2,
< x <-2,
 для -2< x <1.5,
для -2< x <1.5,
 для 1.5< x <+
для 1.5< x <+  .
.
Таким образом, на промежутках (-  ,-2) и (1.5,+
,-2) и (1.5,+  ) функция выпуклая, а на промежутке
) функция выпуклая, а на промежутке
(-2,1.5) – вогнутая, точки  (-2,-124),
(-2,-124),  (-1.5,-8.0625) – точки перегиба.
(-1.5,-8.0625) – точки перегиба.
ПРИМЕР 3. f(x) =  ;
;
Решение. Находим производные:
 ;
;
 , откуда
, откуда  при
при  =0,
=0,  =
= 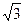 ,
, 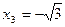 .
.
Знак второй производной определяется знаком величины z = x ( . Так как
. Так как
x ( <0 для -
<0 для -  < x <-
< x <- 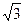 ,
,
x ( >0 для -
>0 для - 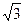 < x <0,
< x <0,
x ( <0 для 0< x <
<0 для 0< x < 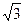 ,
,
x ( >0 для
>0 для 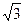 < x <+
< x <+  , то на промежутках (-
, то на промежутках (-  ,-
,- 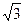 ) и (0,
) и (0, 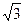 ) функция f(x) вогнутая, а на промежутках (-
) функция f(x) вогнутая, а на промежутках (- 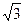 ,0) и (
,0) и (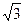 ,+
,+  ) – выпуклая. Точки
) – выпуклая. Точки  (-
(- 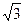 ,
, 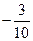 ),
),  (0,0) и
(0,0) и  (
(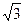 ,
,  ) – точки перегиба.
) – точки перегиба.
ПРИМЕР 4. f(x) = 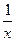 ;
;
Решение. Находим производные:
 ;
;  .
.  не существует. Но при этом при переходе через точку 0 вторая производная меняет свой знак с «минуса» на «плюс», значит, на интервале
не существует. Но при этом при переходе через точку 0 вторая производная меняет свой знак с «минуса» на «плюс», значит, на интервале  функция выпукла вверх и выпукла вниз на интервале
функция выпукла вверх и выпукла вниз на интервале 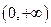 , точка 0 – точка перегиба.
, точка 0 – точка перегиба.

УПРАЖНЕНИЯ
Найти промежутки выпуклости и вогнутости, а также точки перегиба следующих функций:
2.94. f(x) =  ;
;
2.95. f(x) = 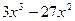 ;
;
2.96. f(x) =  ;
;
2.97. f(x) =  ;
;
2.98. f(x) =  ;
;
2.99. f(x) =  ;
;
2.100. f(x) =  ;
;
2.101.  ;
;
2.102. 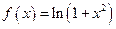 ;
;
2.103.  ;
;
2.104.  ;
;
2.105.  ;
;
2.106.  .
.
Ответы к упражнениям
2.94. (-  ;
;  ) и (1;+
) и (1;+  ) – промежутки выпуклости, (
) – промежутки выпуклости, (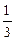 ,1) – промежуток вогнутости,
,1) – промежуток вогнутости,  (
(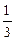 ;
;  ),
),  (1;13) – точки перегиба; 2.95. (-
(1;13) – точки перегиба; 2.95. (-  ;3) – промежуток вогнутости, (3;+
;3) – промежуток вогнутости, (3;+  ) – промежуток выпуклости,
) – промежуток выпуклости,  = (3;-162) – точка перегиба; 2.96. При x <0 кривая вогнута, при x >0 – выпукла,
= (3;-162) – точка перегиба; 2.96. При x <0 кривая вогнута, при x >0 – выпукла,  (0,0) – точка перегиба; 2.97. (-
(0,0) – точка перегиба; 2.97. (-  ;-
;-  ) и (
) и ( ;+
;+  ) – промежутки выпуклости, (-
) – промежутки выпуклости, (-  ;
;  ) – промежуток вогнутости,
) – промежуток вогнутости,  (-
(-  ;-
;-  ),
),  (
( ;-
;-  ) – точки перегиба; 2.98. (-
) – точки перегиба; 2.98. (-  ;-
;-  ) и (
) и ( ;+
;+  ) – промежутки выпуклости, (-
) – промежутки выпуклости, (-  ;
;  ) – промежуток вогнутости,
) – промежуток вогнутости,  (-
(-  ;-2
;-2  ),
),  (
( ;-2
;-2  ) - точки перегиба; 2.99. (-
) - точки перегиба; 2.99. (-  ;-3) и (-1;+
;-3) и (-1;+  ) – промежутки выпуклости, (-3;-1) – промежуток вогнутости,
) – промежутки выпуклости, (-3;-1) – промежуток вогнутости,  (-3;
(-3;  ),
),  (-1;
(-1;  ) - точки перегиба; 2.100. (-
) - точки перегиба; 2.100. (-  ;-1) и (1;+
;-1) и (1;+  ) – промежутки выпуклости, (-1;1) – промежуток вогнутости,
) – промежутки выпуклости, (-1;1) – промежуток вогнутости,
точек перегиба нет. 2.101.  ответ: функция выпукла вверх на промежутке
ответ: функция выпукла вверх на промежутке 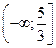 и выпукла вниз на промежутке
и выпукла вниз на промежутке 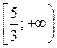 ; точка
; точка  - т. перегиба. 2.102. функция выпукла вверх на промежутках
- т. перегиба. 2.102. функция выпукла вверх на промежутках  и выпукла вниз на промежутке
и выпукла вниз на промежутке  ; точки
; точки  - т. перегиба. 2.103. функция выпукла вверх на промежутке
- т. перегиба. 2.103. функция выпукла вверх на промежутке  и выпукла вниз на промежутке
и выпукла вниз на промежутке  ; точка
; точка  - т. перегиба. 2.104. т. перегиба нет; функция выпукла вверх при х<-1 и выпукла вниз при х>-1. 2.105. т. перегиба
- т. перегиба. 2.104. т. перегиба нет; функция выпукла вверх при х<-1 и выпукла вниз при х>-1. 2.105. т. перегиба  . 2.106. т. перегиба
. 2.106. т. перегиба 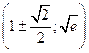 ; функция выпукла вверх при
; функция выпукла вверх при  и выпукла вниз при
и выпукла вниз при  .
.
Асимптоты
Прямая линия называется асимптотой для кривой y=f(x), если расстояние от точки M (x,y), лежащей на кривой, до этой прямой стремится к нулю при движении точки М вдоль какой-нибудь ветви кривой в бесконечность.
Различают три вида асимптот: вертикальные (рис.2.13), горизонтальные (рис.2.14), наклонные (рис.2.15).
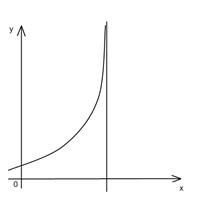

Рис.2.13 Рис.2.14
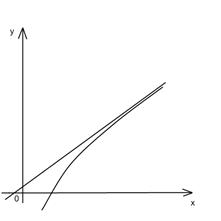
Рис.2.15
Вертикальные асимптоты. Если хотя бы один из пределов функции f(x) в точке a справа или слева равен бесконечности, то прямая x = a – вертикальная асимптота.
Горизонтальные асимптоты. Если существуют пределы  f(x) =
f(x) =  и
и  f(x) =
f(x) =  , то прямая y =
, то прямая y =  - правая горизонтальная асимпто та, y =
- правая горизонтальная асимпто та, y =  - левая горизонтальная асимптота.
- левая горизонтальная асимптота.
Наклонные асимптоты. Если существуют пределы

 =
=  ,
,  (f(x) -
(f(x) -  x) =
x) = 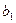 , то прямая y =
, то прямая y =  x +
x + 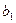 , - наклонная правая асимптота.
, - наклонная правая асимптота.
Если существуют пределы

 =
=  ,
,  (f(x) -
(f(x) -  x) =
x) =  , то прямая y =
, то прямая y =  x +
x +  , - наклонная левая асимптота.
, - наклонная левая асимптота.
РЕШЕНИЕ ЗАДАЧ
Найдем асимптоты функций.
ПРИМЕР 1. y = 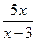 ;
;
Решение.
1. Найдем вертикальные асимптоты. Область определения функции не включает точку x =3. Проверим, что в этой точке график f(x) имеет вертикальную асимптоту:
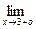
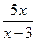 = +
= +  ,
,

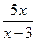 = -
= -  .
.
По определению, x=3 – вертикальная асимптота.
2. Исследуем на горизонтальные асимптоты:
 f(x) =
f(x) = 
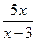 =
= 
 ,
,
 f(x) =
f(x) = 
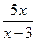 =
= 
 , таким образом, кривая имеет горизонтальную асимптоту: y =5.
, таким образом, кривая имеет горизонтальную асимптоту: y =5.
3. Исследуем на наклонные асимптоты. В данном случае они совпадут с горизонтальными. Покажем это:

 =
= 
 =
= 
 =0, аналогично
=0, аналогично 
 =0 – поэтому угловой коэффициент равен 0, и наклонные асимптоты являются горизонтальными.
=0 – поэтому угловой коэффициент равен 0, и наклонные асимптоты являются горизонтальными.
ПРИМЕР 2. y =  ;
;
Решение.
1. Найдем вертикальные асимптоты. Область определения функции не включает точку x =1. Проверим, что в этой точке график f(x) имеет вертикальную асимптоту:
Так как
 f(x) =
f(x) = 
 = +
= +  ,
,
 f(x) =
f(x) = 
 = -
= -  ,
,
то по определению кривая имеет вертикальную асимптоту x =1.
2. Найдем горизонтальные асимптоты:
 f(x) =
f(x) = 
 = +
= +  ,
,
 f(x) =
f(x) = 
 = -
= -  , поэтому горизонтальных асимптот нет.
, поэтому горизонтальных асимптот нет.
2. Найдем наклонные асимптоты
 =
= 
 =
= 
 =3,
=3,
 =
= 
 =
= 
 =3=
=3=  , т.е. существует наклонная асимптота с угловым коэффициентом k =3.
, т.е. существует наклонная асимптота с угловым коэффициентом k =3.
Находим 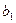 ,
,  :
:
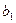 =
=  (f(x) -
(f(x) -  x) =
x) = 
 ,
,
 =
=  (f(x) -
(f(x) -  x) =
x) = 
 , следовательно существует наклонная асимптота y =3 x +3.
, следовательно существует наклонная асимптота y =3 x +3.
УПРАЖНЕНИЯ
Найти асимптоты:
2.107. y=  ;
;
2.108. y=  ;
;
2.109. y=  .
.
2.110. y=  ;
;
2.111. y=  ;
;
2.112. y= 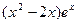 ;
;
2.113. y=  ;
;
2.114.  ;
;
2.115.  ;
;
2.116. 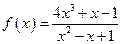 ;
;
2.117.  .
.
Ответы к упражнениям
2.107. y =2 - горизонтальная асимптота; 2.108. x =3 - вертикальная асимптота, y = x -3 – наклонная асимптота; 2.109. x =1 – вертикальная асимптота, y =2 – горизонтальная асимптота; 2.110. x =1 – вертикальная асимптота, y =2 x +1 – наклонная асимптота; 2 .111. y = x +1 и y = -3 x -1 – наклонные асимптоты; 2.112. y = 0 – горизонтальная асимптота; 2.113. y = -1, y =1 – горизонтальные асимптоты. 2.114. х=-1 - вертикальная асимптота; у=х-2 – наклонная асимптота; 2.115. х=0 - вертикальная асимптота;  - горизонтальная асимптота; 2.116. y=4x+4 – наклонная асимптота; 2.117. х=0 - вертикальная асимптота; y=x – наклонная асимптота.
- горизонтальная асимптота; 2.116. y=4x+4 – наклонная асимптота; 2.117. х=0 - вертикальная асимптота; y=x – наклонная асимптота.
Date: 2016-05-17; view: 1571; Нарушение авторских прав