
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры рядов Тейлора
|
|
1. Пусть 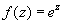 . Эта функция как известно, голоморфна во всей комплексной плоскости. Это гарантирует, что любой круг вписывается в область голоморфности этой функции.
. Эта функция как известно, голоморфна во всей комплексной плоскости. Это гарантирует, что любой круг вписывается в область голоморфности этой функции.
Возьмем 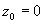 , тогда для любого
, тогда для любого  из любого круга с центром в нуле будем иметь
из любого круга с центром в нуле будем иметь
 .
.
Это значит, что ряд Тейлора совпадает с показательной функцией при любом  .
.
2. Пусть 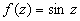 . Эта функция голоморфна во всей комплексной плоскости. Возьмем
. Эта функция голоморфна во всей комплексной плоскости. Возьмем 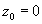 , тогда
, тогда
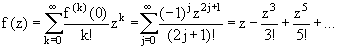
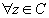 .
.
В самом деле, производные синуса легко вычислить, причем очевидна периодичность по 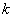 : производная порядка
: производная порядка 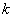 совпадает с производной порядка
совпадает с производной порядка 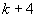
| k | 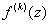
| 
|
| Sin(z) | ||
| Cos(z) | ||
| -Sin(z) | ||
| -Cos(z) | -1 | |
| Sin(z) |
Производные четного порядка равны нулю при  . По этой причине соответствующие члены ряда Тейлора мы просто пропускаем. Члены ряда с нечетными номерами отличны от нуля, поэтому они, занумерованные подряд с помощью индекса
. По этой причине соответствующие члены ряда Тейлора мы просто пропускаем. Члены ряда с нечетными номерами отличны от нуля, поэтому они, занумерованные подряд с помощью индекса 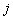 , в окончательной формуле и фигурируют. Выражение
, в окончательной формуле и фигурируют. Выражение  появилось от того, что как видно из таблицы знаки производных нечетного порядка чередуются.
появилось от того, что как видно из таблицы знаки производных нечетного порядка чередуются.
3. 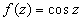 . Этот пример аналогичен предыдущему. Опять возьмем
. Этот пример аналогичен предыдущему. Опять возьмем 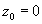 . Тогда
. Тогда
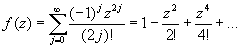
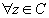
Здесь производные нечетного порядка оказались равными нулю при  , а у четных производных чередуются знаки.
, а у четных производных чередуются знаки.
| k | 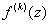
| 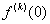
|
| Cos(z) | ||
| -Sin(z) | ||
| -Cos(z) | -1 | |
| Sin(z) | ||
| Cos(z) |
8. НУЛИ ГОЛОМОРФНЫХ ФУНКЦИЙ
Первая теорема единственности. Если функция 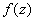 голоморфна в области G и в некоторой точке
голоморфна в области G и в некоторой точке 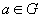 сама функция и все ее производные равны нулю, то функция равна нулю во всей области G.
сама функция и все ее производные равны нулю, то функция равна нулю во всей области G.
Доказательство. Представим функцию 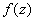 в виде ряда Тейлора в круге с центром в точке
в виде ряда Тейлора в круге с центром в точке  .
.
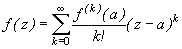 .
.
Поскольку все производные в точке  равны нулю, то сумма ряда Тейлора тоже будет равна нулю. Следовательно,
равны нулю, то сумма ряда Тейлора тоже будет равна нулю. Следовательно,  Мы доказали, что
Мы доказали, что  в выбранном круге. В частности, в этом круге равны нулю и все производные функции
в выбранном круге. В частности, в этом круге равны нулю и все производные функции 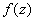 .
.
Пусть теперь z – любая точка G. В силу связности G ее можно соединить ломаной с точкой a. Обозначим через R расстояние от ломаной до границы области G. Разобьем ломаную на отрезки длиной меньшей  точками
точками 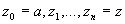 Круг радиуса
Круг радиуса  с центром в любой точке
с центром в любой точке  будет целиком
будет целиком
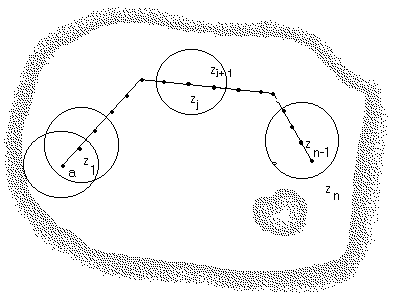
лежать в G.
С помощью точки 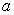 доказано, что в точке
доказано, что в точке  функция и все ее производные равны нулю.
функция и все ее производные равны нулю.
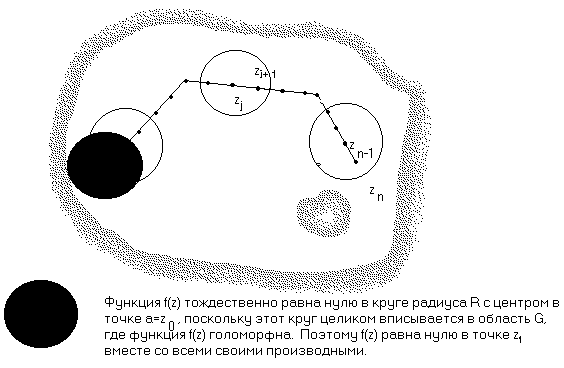
Повторяя те же рассуждения для круга с центром в  , получим, что в
, получим, что в  функция и все ее производные равны нулю.
функция и все ее производные равны нулю.

За конечное число шагов покажем, что этим же свойством обладает и точка  .
.
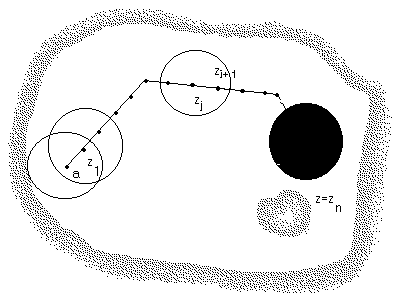
Теорема доказана.
Следствие. Если две голоморфные в области G функции 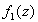 и
и  совпадают в точке
совпадают в точке 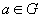 и имеют в ней одинаковые производные, то они совпадают во всей области G. Доказательство состоит в применении предыдущей теоремы к функции
и имеют в ней одинаковые производные, то они совпадают во всей области G. Доказательство состоит в применении предыдущей теоремы к функции 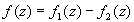 .
.
Заметим, что в обычном анализе нет аналога доказанной теоремы.
Например, функция 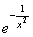 , доопределенная нулем в нуле, имеет все производные в точке x = 0, равные нулю.
, доопределенная нулем в нуле, имеет все производные в точке x = 0, равные нулю.
Нуль, порядок (кратность) нуля. Точка, в которой голоморфная функция равна нулю, называется нулем функцию. То есть, если a – нуль функции 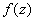 , то
, то  , если при этом
, если при этом  , то нуль называется простым. Если
, то нуль называется простым. Если 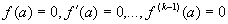 , но
, но  , то число k называется кратностью или порядком нуля.
, то число k называется кратностью или порядком нуля.
Из первой теоремы единственности следует, что если голоморфная функция не равна тождественно нулю, то найдется производная некоторого порядка, отличная от нуля, в точке a. Следовательно, всякий нуль голоморфной функции имеет конечную кратность.
Пусть a – нуль кратности k функции 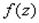 . Применим формулу Тейлора при n=k-1. Так как
. Применим формулу Тейлора при n=k-1. Так как  , то
, то
 (8.1)
(8.1)
где 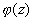 голоморфна в точке
голоморфна в точке  , и
, и 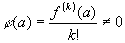 , в силу (7.4) из §7.
, в силу (7.4) из §7.
Итак, в окрестности нуля кратности k функция представима в виде (8.1), где 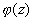 – голоморфна и отлична от нуля в точке
– голоморфна и отлична от нуля в точке 
Обратно, если функция представима в описанном виде, то дифференцированием проверяется, что  и
и  , т.е. функция
, т.е. функция 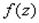 имеет в точке a нуль кратности k.
имеет в точке a нуль кратности k.
Важное следствие. Нули голоморфной функции, не равной тождественно нулю, являются изолированными точками.
Действительно, так как 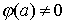 и функция
и функция 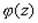 голоморфна, а значит и непрерывна, в окрестности точки
голоморфна, а значит и непрерывна, в окрестности точки 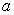 , то найдется окрестность, в которой
, то найдется окрестность, в которой  . В этой окрестности при
. В этой окрестности при 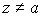 оба множителя справа http://62.76.174.9/Courses/matfak/01/r8.html?AICC_SID=913571621-12311&AICC_URL=http%3A%2F%2Flssrv.main.vsu.ru%2FLearningSpace5%2FProgram%2FScripts%2FTrack.asp - 81отличны от нуля и, следовательно,
оба множителя справа http://62.76.174.9/Courses/matfak/01/r8.html?AICC_SID=913571621-12311&AICC_URL=http%3A%2F%2Flssrv.main.vsu.ru%2FLearningSpace5%2FProgram%2FScripts%2FTrack.asp - 81отличны от нуля и, следовательно, 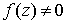 при
при 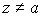 .
.
Вторая теорема единственности. Если голоморфная в области G функция  обращается в нуль на множестве, имеющем точку сгущения лежащую внутри G, то она тождественно равна нулю во всей области G.
обращается в нуль на множестве, имеющем точку сгущения лежащую внутри G, то она тождественно равна нулю во всей области G.
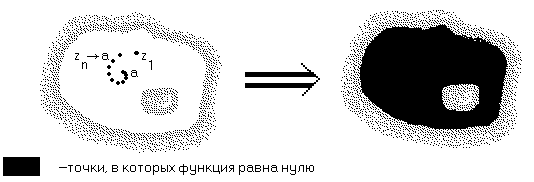
Доказательство. Обозначим точку сгущения, о которой идет речь, через a. По условию 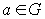 и существует такая последовательность
и существует такая последовательность 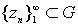 , что и
, что и  ,
, 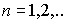 в силу непрерывности
в силу непрерывности 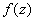 в G
в G
 .
.
Отсюда вытекает, что точка a является неизолированным нулем функции 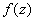 .По предыдущему следствию это возможно лишь тогда, когда функция
.По предыдущему следствию это возможно лишь тогда, когда функция 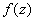 тождественно равна нулю в окрестности точки a. В силу первой теоремы единственности
тождественно равна нулю в окрестности точки a. В силу первой теоремы единственности  во всей области G. Теорема доказана.
во всей области G. Теорема доказана.
Следствие. Если две голоморфные в области G функции 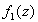 и
и  совпадают на множестве, имеющем точку сгущения внутри G, то они совпадают во всей G.
совпадают на множестве, имеющем точку сгущения внутри G, то они совпадают во всей G.
Для доказательства нужно применить предыдущую теорему к функции 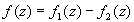 .
.
Приведенное следствие чрезвычайно полезно, если нам требуется доказать некоторое равенство, содержащее голоморфные функции, то достаточно его проверить на некотором множестве, имеющем точку сгущения, например, на отрезке вещественной оси, входящем в область голоморфной функции. После этого можно утверждать, что равенство справедливо во всей области. Этим можно пользоваться, например, при доказательстве тригонометрических тождеств.
9. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
Возьмем окрестность некоторой точки и отбросим саму точку. Полученную неодносвязную область сокращенно
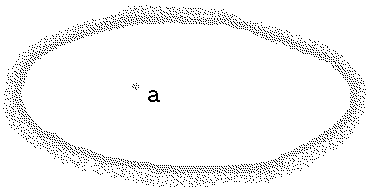
называют проколотой окрестностью точки a.
Точка a называется изолированной особой точкой функции 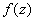 , если эта функция голоморфна в проколотой окрестности этой точки и в самой точке либо не
, если эта функция голоморфна в проколотой окрестности этой точки и в самой точке либо не
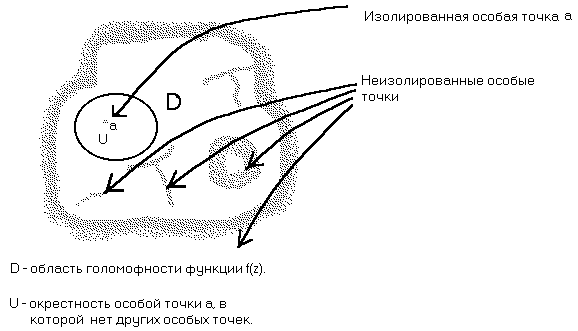
определена, либо определена, но не голоморфна. Различают три типа изолированных особых точек.
1. Устранимая особенность. Изолированная особая точка  называется устранимой, если существует конечный предел
называется устранимой, если существует конечный предел
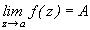 (9.1)
(9.1)
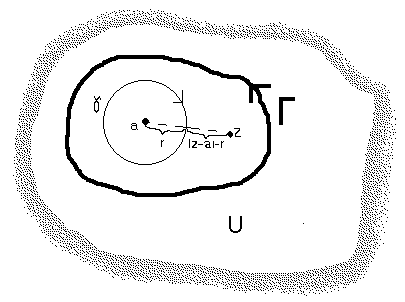
Зафиксируем точку z в U. Выберем такой контур Г, чтобы точки a и z лежали внутри его, и
окружность  с центром точке
с центром точке  и с настолько малым радиусом r, чтобы точка z лежала вне этой окружности. Применяя интегральную формулу Коши для двусвязной области, ограниченной
и с настолько малым радиусом r, чтобы точка z лежала вне этой окружности. Применяя интегральную формулу Коши для двусвязной области, ограниченной 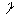 и Г, содержащей z, получаем
и Г, содержащей z, получаем
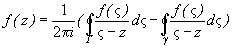 (9.2)
(9.2)
пользуясь (9.1),оценим второй интеграл:
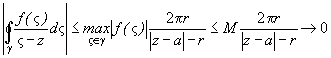 при
при 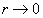
(Мы воспользовались тем, что наименьшее расстояние от точки z до точек окружности 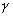 равно расстоянию до центра минус радиус r). Переходя к пределу при
равно расстоянию до центра минус радиус r). Переходя к пределу при 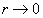 в равенстве (9.2), получаем
в равенстве (9.2), получаем
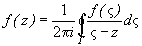
Интеграл справа является интегралом типа Коши и, как было сказано в §6, он определяет голоморфную внутри Г функцию. Из равенства следует, что исходная функция совпадает с этой голоморфной функцией внутри Г за исключением, быть может, точки  . Доопределим функцию
. Доопределим функцию 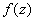 в точке
в точке  равенством
равенством

Так определенная функция будет уже голоморфной и в точке  . Таким образом, если
. Таким образом, если  является устранимой особой точкой функции
является устранимой особой точкой функции 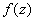 , то функция может быть доопределена в этой точке так, то она будет голоморфной и в точке
, то функция может быть доопределена в этой точке так, то она будет голоморфной и в точке  (особенность устраняется).
(особенность устраняется).
2. Полюс. Изолированная особая точка функции 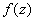 называется полюсом, если
называется полюсом, если 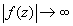 при
при  . Из определения следует, что для всякого положительного числа существует окрестность точки
. Из определения следует, что для всякого положительного числа существует окрестность точки  , в которой модуль функции не меньше этого числа. Пусть, например, при
, в которой модуль функции не меньше этого числа. Пусть, например, при  выполняется неравенство
выполняется неравенство 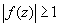 . Рассмотрим функцию
. Рассмотрим функцию 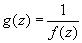 . Эта функция будет голоморфной в проколотой окрестности точки
. Эта функция будет голоморфной в проколотой окрестности точки  , так как в ней голоморфна
, так как в ней голоморфна 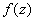 и
и 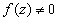 . Далее
. Далее
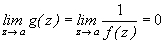 ,
,
Значит функция  имеет в точке
имеет в точке  устранимую особенность. Тогда ее можно доопределить в точке
устранимую особенность. Тогда ее можно доопределить в точке  так, что она станет голоморфной, а значит и непрерывной, в точке
так, что она станет голоморфной, а значит и непрерывной, в точке  . Полагаем
. Полагаем
 .
.
Так доопределенная функция  будет голоморфной в точке
будет голоморфной в точке  и будет иметь в ней нуль. Пусть
и будет иметь в ней нуль. Пусть 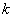 - порядок этого нуля, тогда, как показано в (9.1) в §8, функция
- порядок этого нуля, тогда, как показано в (9.1) в §8, функция  в окрестности точки
в окрестности точки  представима в виде
представима в виде
 ,
,
где 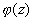 - голоморфна в этой окрестности и
- голоморфна в этой окрестности и  . Тогда
. Тогда
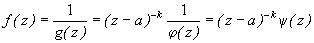 . (9.3)
. (9.3)
Так как  , то функция
, то функция 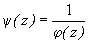 голоморфна в более узкой, возможно, окрестности точки
голоморфна в более узкой, возможно, окрестности точки  . Кроме того
. Кроме того  .
.
Обратно, если в окрестности точки  функция
функция 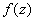 представима в виде (9.3), где
представима в виде (9.3), где 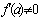 голоморфна в
голоморфна в  и
и 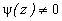 , то при
, то при 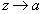 первый множитель справа по модулю неограниченно возрастает, а второй стремится к
первый множитель справа по модулю неограниченно возрастает, а второй стремится к 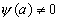 . Следовательно,
. Следовательно, 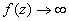 при
при 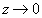 и точка
и точка  является полюсом
является полюсом 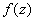 .
.
Итак, для того, чтобы точка  была полюсом функции
была полюсом функции 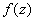 необходимо и достаточно, чтобы она была представима в виде
необходимо и достаточно, чтобы она была представима в виде
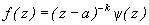 ,
,
где 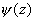 - голоморфна в окрестности
- голоморфна в окрестности  и
и 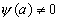 .
.
Число 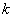 называется тогда кратностью или порядком полюса
называется тогда кратностью или порядком полюса  .
.
Из предыдущего ясно, что, если функция 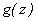 имеет в точке
имеет в точке  нуль кратности
нуль кратности 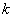 , то
, то  имеет в точке
имеет в точке  полюс порядка
полюс порядка 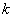 и обратно.
и обратно.
3. Существенно особая точка. Изолированная особая точка функции  называется существенно особой, если она не является ни устранимой особенностью, ни полюсом.
называется существенно особой, если она не является ни устранимой особенностью, ни полюсом.
Теорема Пикара В любой окрестности существенно особой точки функции 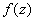 эта функция принимает все возможные комплексные значения, за исключением быть может одного.
эта функция принимает все возможные комплексные значения, за исключением быть может одного.
Эта теорема доказывается довольно сложно и здесь приводится без доказательства.
Функция  имеет существенно особую точку
имеет существенно особую точку 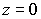 и принимает все комплексные значения кроме числа
и принимает все комплексные значения кроме числа 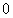 . Это говорит о том, что утверждение теоремы Пикара нельзя уточнить.
. Это говорит о том, что утверждение теоремы Пикара нельзя уточнить.
Date: 2016-01-20; view: 606; Нарушение авторских прав