
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комплекснозначные функции действительного переменного. Кривые на комплексной области
|
|
Комплексные функции действительного переменного. Пусть каждой точке t отрезка [a,b] на действительной оси поставлено в соответствие число Z(t), если разложить число Z(t) на действительную и мнимую части Z(t)=х(t)+iy(t),то возникнут две действительные функции одного действительного переменного х(t) и y(t). Если эти функции непрерывны в точке  [a,b],то и функция Z(t) непрерывна в том смысле, что
[a,b],то и функция Z(t) непрерывна в том смысле, что  при
при 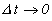 . Если функции х(t) и y(t) дифференцируемы, то функция Z(t) также дифференцируема в том смысле, что существует
. Если функции х(t) и y(t) дифференцируемы, то функция Z(t) также дифференцируема в том смысле, что существует
 .
.
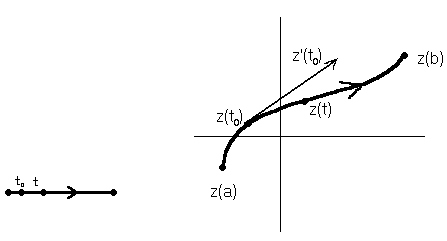
Справедливы и обратные утверждения.
Все правила вычисления производных вытекают из свойств пределов, поэтому
-
 ;
; -
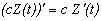 (с ― комплексное число);
(с ― комплексное число); -
 ;
; -
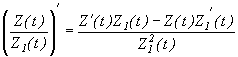 , если
, если  .
.
Здесь предполагалось, что  —дифференцируемы.
—дифференцируемы.
Заметим еще, что для кусочно-непрерывной функции  = х(t) + iy(t) определяется интеграл
= х(t) + iy(t) определяется интеграл
 =
=  + i
+ i  ,
,
обладающий всеми свойствами обычного интеграла Римана.
Можно проверить, что комплексный постоянный множитель можно вносить под знак интеграла.
Вместо одного равенства интеграл можно эквивалентно определить двумя
 =
=  ,
,  =
=  ,
,
Иными словами, знаки Re и Im можно вносить под знак интеграла.
Рассмотрим теперь модуль интеграла. Обозначим

Пусть  И пусть argI=
И пусть argI=  . Тогда
. Тогда
I (cos  - i sin
- i sin  )=
)= 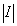 (cos
(cos  + i sin
+ i sin  )(cos
)(cos  - i sin
- i sin  )=
)= 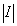 .
.
Отсюда

(постоянный множитель внесли под знак интеграла).
Далее
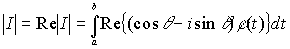 .
.
Действительная часть комплексного числа не превосходит его модуля, а определённый интеграл не меняет знака неравенства, поэтому

Таким образом
 . (4.1)
. (4.1)
Отметим ещё, что справедлива формула Ньютона-Лейбница

или, окончательно
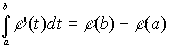 .
.
Кривые на комплексной плоскости. Непрерывное отображение отрезка  действительной оси в комплексную плоскость называется путём. Записывать это отображение можно так:
действительной оси в комплексную плоскость называется путём. Записывать это отображение можно так:  или в комплексной форме
или в комплексной форме 
 Точка
Точка  называется началом пути, точка
называется началом пути, точка  - концом пути. Таким образом, путь определяется комплекснозначной функцией действительного переменного
- концом пути. Таким образом, путь определяется комплекснозначной функцией действительного переменного  . Два пути
. Два пути 
 и
и 
 называются эквивалентными, если существует такое монотонно возрастающее отображение
называются эквивалентными, если существует такое монотонно возрастающее отображение  отрезка
отрезка  на отрезок
на отрезок 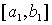 , что
, что  , при этом
, при этом  и
и 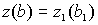 .
.

Совокупность всех взаимно эквивалентных путей называется кривой. Кривую мы обычно будем обозначать одной буквой, например,  . Каждый путь из этого класса называется представляющим путём кривой
. Каждый путь из этого класса называется представляющим путём кривой  . Для эквивалентных путей множества значений функций
. Для эквивалентных путей множества значений функций  и
и 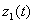 совпадают, поэтому можно говорить о множестве точек кривой, которое будем обозначать через
совпадают, поэтому можно говорить о множестве точек кривой, которое будем обозначать через  . Иногда его называют образом пути. Кроме того, на кривой определяется направление движения по образу пути по мере возрастания аргумента
. Иногда его называют образом пути. Кроме того, на кривой определяется направление движения по образу пути по мере возрастания аргумента  . Это направление не зависит от выбора представляющего пути кривой и будет отмечаться стрелочкой на рисунках.
. Это направление не зависит от выбора представляющего пути кривой и будет отмечаться стрелочкой на рисунках.
Кривая называется замкнутой, если её начало и конец совпадают. Понятие непрерывной кривой является слишком общим в том смысле, что оно не всегда соответствует нашему интуитивному понятию кривой. Так, например, построены кривые, множество точек которых совпадают с квадратом на плоскости (кривая Пеано). Более естественным объектом являются простые или жордановы кривые. Кривая называется простой или жордановой, если для её представителей (путей) 
 отображение
отображение  на полуинтервале
на полуинтервале  взаимно однозначно. Такая кривая может быть замкнутой, если
взаимно однозначно. Такая кривая может быть замкнутой, если  или незамкнутой, если
или незамкнутой, если  . Геометрически, это означает, что кривая без самопересечений.
. Геометрически, это означает, что кривая без самопересечений.
Глубоким фактом является
Теорема Жордана. Всякая жорданова замкнутая кривая  разбивает оставшуюся часть плоскости на две непересекающиеся области: внутреннюю, которая обозначается
разбивает оставшуюся часть плоскости на две непересекающиеся области: внутреннюю, которая обозначается  – ограниченную и внешнюю, которая обозначается
– ограниченную и внешнюю, которая обозначается 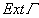 – неограниченную.
– неограниченную.

Доказательство этой теоремы сложно и здесь не приводится.
Для дальнейшего полезно следующее определение.
Область  на плоскости называется односвязной, если для любой замкнутой жордановой кривой, лежащей в
на плоскости называется односвязной, если для любой замкнутой жордановой кривой, лежащей в  , ее внутренность тоже принадлежит
, ее внутренность тоже принадлежит  .
.

Геометрически понятие односвязности означает, что область "не имеет дыр". Если в области одна дыра, то она называется двусвязной и т.д.

Жордановы замкнутые кривые еще называют жордановыми контурами.


Путь 
 называется гладким, если функция
называется гладким, если функция  - непрерывно дифференцируема и
- непрерывно дифференцируема и  при каждом
при каждом  . Путь называется кусочно-гладким, если отрезок
. Путь называется кусочно-гладким, если отрезок  можно так разбить на конечное число отрезков, что сужение
можно так разбить на конечное число отрезков, что сужение  на каждый из этих отрезков даёт гладкий путь. Кривая называется гладкой (кусочно-гладкой), если у неё есть гладкий (кусочно-гладкий) представляющий путь.
на каждый из этих отрезков даёт гладкий путь. Кривая называется гладкой (кусочно-гладкой), если у неё есть гладкий (кусочно-гладкий) представляющий путь.
Из курса анализа известно, что кусочно-гладкая кривая является спрямляемой, т.е. имеет конечную длину, вычисляемую с помощью интеграла по формуле

или в комплексной форме
 . (4.2)
. (4.2)
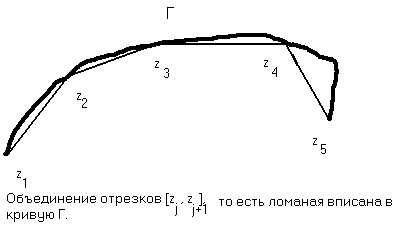
Через  мы будем обозначать длину кривой, которая по определению равна точной верхней грани длин вписанных в данную кривую ломаных.
мы будем обозначать длину кривой, которая по определению равна точной верхней грани длин вписанных в данную кривую ломаных.
Date: 2016-01-20; view: 1742; Нарушение авторских прав