
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Интеграл функций комплексного переменного по кривой
|
|
Пусть 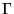 - кусочно-гладкая кривая и
- кусочно-гладкая кривая и 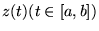 представляющий ее кусочно гладкий путь. Предположим, что на множестве точек кривой
представляющий ее кусочно гладкий путь. Предположим, что на множестве точек кривой 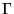 определена непрерывная функция
определена непрерывная функция  Интегралом от функции
Интегралом от функции  по кривой
по кривой 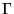 называют величину
называют величину

| (5.1) |
(Иногда вместо "интеграл по кусочно-гладкой кривой 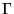 " говорят "интеграл по контуру
" говорят "интеграл по контуру 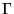 ")
")
В силу непрерывности сложной функции  и кусочной гладкости
и кусочной гладкости  функция
функция  будет кусочно непрерывной и, следовательно, интеграл от нее определен.
будет кусочно непрерывной и, следовательно, интеграл от нее определен.

Заметим еще, что этот интеграл не зависит от выбора кусочно гладкого пути, представляющего 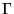 . Действительно, если кусочно гладкий путь
. Действительно, если кусочно гладкий путь  эквивалентен пути
эквивалентен пути  и функция
и функция 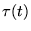 осуществляет эту эквивалентность:
осуществляет эту эквивалентность:  , то под интегралом справа в (5.1) можно сделать замену переменного
, то под интегралом справа в (5.1) можно сделать замену переменного  . Тогда, используя правило замены переменного и формулу производной сложной функции, получаем
. Тогда, используя правило замены переменного и формулу производной сложной функции, получаем

Таким образом, определение (5.1) корректно.
Из свойств определенного интеграла непосредственно вытекают свойства интеграла (5.1).
1. Интеграл суммы двух функций по кривой 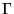 равен сумму их интегралов по этой кривой.
равен сумму их интегралов по этой кривой.
2. Постоянный (комплексный) множитель выносится за знак интеграла.
3. Если на кривой поменять направление на противоположное. Вместо пути  взять путь
взять путь 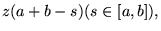 то интеграл меняет знак.
то интеграл меняет знак.

4. Если кривая разбита на две части  и
и  , то интеграл по всей кривой равен сумме интегралов по ее частям
, то интеграл по всей кривой равен сумме интегралов по ее частям


Если кривая  замкнута, то интеграл по ней записывается в виде
замкнута, то интеграл по ней записывается в виде

Примеры вычисления интегралов.
1.  , тогда
, тогда
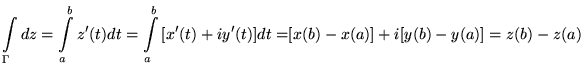
| (5.2) |
Если кривая замкнута, то  и
и

2.  .
.
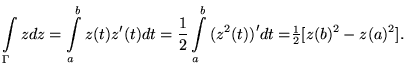
Мы воспользовались тем, что

Для замкнутой кривой

| (5.3) |
3. Пусть 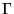 - окружность с центром в точке
- окружность с центром в точке 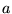 и радиуса
и радиуса  с выбранным на ней направлением против часовой стрелки. В качестве пути, представляющего данную кривую можно выбрать отображение отрезка
с выбранным на ней направлением против часовой стрелки. В качестве пути, представляющего данную кривую можно выбрать отображение отрезка 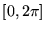 в
в  вида
вида

.

Действительно,  и, следовательно, точка
и, следовательно, точка  пробегает окружность в заданном направлении.
пробегает окружность в заданном направлении.
Пусть теперь  . Тогда с помощью формулы Муавра получаем
. Тогда с помощью формулы Муавра получаем



Если  , то в силу периодичности cos и sin, справа получается нуль. Если же
, то в силу периодичности cos и sin, справа получается нуль. Если же  , то нужно остановиться на предпоследнем равенстве, из которого видно, что стоящая в нем величина равна
, то нужно остановиться на предпоследнем равенстве, из которого видно, что стоящая в нем величина равна  .
.
Таким образом,

при  , и
, и

| (5.4) |
Эти интегралы играют важную роль в дальнейшем.
Оценка интеграла. Из определения (5.1) и неравенства (4.1) из параграфа 4 получаем

Из свойств определенного интеграла и формулы (4.2) вытекает, что

| (5.5) |
Аппроксимация интеграла интегральной суммой. Пусть 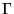 кривая с кусочно-гладким определяющим путем
кривая с кусочно-гладким определяющим путем  , где (
, где ( ). Разобьем отрезок [a,b] на части точками
). Разобьем отрезок [a,b] на части точками  . Точки
. Точки 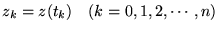 тогда разбивают кривую на части, которые обозначаем через
тогда разбивают кривую на части, которые обозначаем через  .
.
Составим интегральную сумму
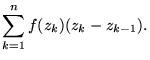
| (5.6) |

Мы хотим сравнить эту сумму с интегралом  по кривой
по кривой 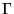 .
.
Для этого преобразуем (5.6) в силу (5.2)

С другой стороны, по свойствам интеграла

Поэтому


В силу равномерной непрерывности функции  для любого
для любого  при достаточно мелком разбиении кривой
при достаточно мелком разбиении кривой 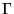 на части имеем
на части имеем

Тогда

Таким образом, интеграл от функции  по кривой
по кривой 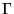 может быть с любой точностью аппроксимирован интегральной суммой.
может быть с любой точностью аппроксимирован интегральной суммой.
Аппроксимация интеграла по кривой интегралом по ломаной. Предположим теперь, что функция  определена и непрерывна не только на кривой
определена и непрерывна не только на кривой 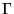 , но и в некоторой области
, но и в некоторой области  , содержащей кривую
, содержащей кривую 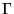 . Разобьем кривую
. Разобьем кривую 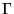 на конечное число частей
на конечное число частей  точками
точками  . Выберем разбиение столь мелким, чтобы все круги
. Выберем разбиение столь мелким, чтобы все круги  лежали в
лежали в  и чтобы в этих кругах выполнялись неравенства
и чтобы в этих кругах выполнялись неравенства

| (5.7) |
где  заданное число.
заданное число.
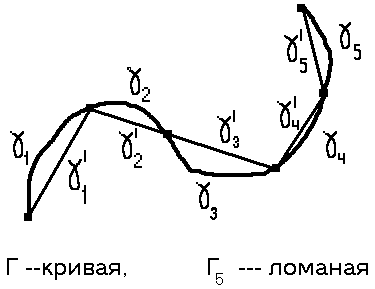
Обозначим через  ломаную с вершинами в точках
ломаную с вершинами в точках  (в порядке следования), а через
(в порядке следования), а через  её звенья, соединяющие точки
её звенья, соединяющие точки  и
и  . Сравним интегралы от функции
. Сравним интегралы от функции  по кривой
по кривой  и по ломаной
и по ломаной 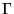
 . Имеем
. Имеем

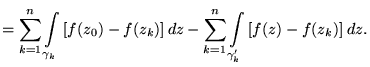
Здесь мы воспользовались тем, что

Из предыдущего получаем

кривая  и отрезок
и отрезок  лежат в круге, где выполнено неравенство (5.7) и, кроме того
лежат в круге, где выполнено неравенство (5.7) и, кроме того  , поэтому
, поэтому

Таким образом, при достаточно малом разбиении интеграл по ломаной  сколько угодно близок к интегралу по кривой
сколько угодно близок к интегралу по кривой 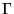 .
.
Date: 2016-01-20; view: 1474; Нарушение авторских прав