
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференцируемость функции в смысле комплексного анализа
|
|
Дифференцируемость в точке, производная. Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности  точки
точки  . Если
. Если  , то
, то  - приращение функции
- приращение функции  в точке
в точке  .
.
Рассматривается предел

| (3.1) |
Если он существует, то по аналогии с обычным анализом он называется производной функции  в точке
в точке  и обозначается через
и обозначается через 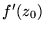 , а функция
, а функция  называется дифференцируемой в точке
называется дифференцируемой в точке  . Однако в этом определении имеется существенная особенность. Приращение
. Однако в этом определении имеется существенная особенность. Приращение  , как и любое комплексное число, имеет модуль
, как и любое комплексное число, имеет модуль  и аргумент
и аргумент  :
: 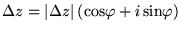 . Под знаком предела написано
. Под знаком предела написано  , то есть предполагается, что предел не зависит от
, то есть предполагается, что предел не зависит от  , то есть он не зависит от того пути, по которому точка
, то есть он не зависит от того пути, по которому точка  приближается к точке
приближается к точке  . Для того, чтобы подчеркнуть это, при существовании предела (3.1) в указанном смысле говорят, что функция
. Для того, чтобы подчеркнуть это, при существовании предела (3.1) в указанном смысле говорят, что функция  дифференцируема в точке
дифференцируема в точке  в смысле комплексного анализа.
в смысле комплексного анализа.

Вспоминая определение предела, для дифференцируемой  можно записать
можно записать

где  при
при  , или
, или

| (3.2) |
(Отсюда, в частности, следует, что дифференцируемая в точке функция непрерывна в этой точке, потому что приращение функции будет стремится к нулю при стремлении к нулю приращения аргумента.)
Обозначая  , получаем
, получаем

где  при
при  .
.
Уравнения Коши-Римана. Пусть функция  в смысле комплексного анализа в точке
в смысле комплексного анализа в точке  . Рассмотрим во что выльются наши определения, если мы будем рассматривать только вещественные приращения, то есть приращения только по
. Рассмотрим во что выльются наши определения, если мы будем рассматривать только вещественные приращения, то есть приращения только по  , или только чисто мнимые приращения, то есть приращения только по
, или только чисто мнимые приращения, то есть приращения только по 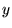 . Итак, пусть сначала
. Итак, пусть сначала 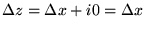 . Тогда
. Тогда
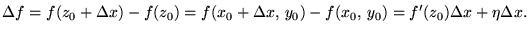
Поэтому

И, следовательно,
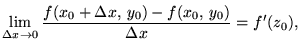
| (3.3) |
так как  при
при 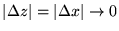 .
.
Это означает, что функция 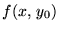 одной переменной
одной переменной  имеет производную в точке
имеет производную в точке  . Эта производная по переменной
. Эта производная по переменной  называется частной производной по
называется частной производной по  и обозначается
и обозначается

То есть по определению частной производной

Поэтому, в силу (3.3) частная производная  существует и
существует и

| (3.4) |
Рассмотрим теперь приращение вдоль оси 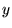 , то есть пусть
, то есть пусть  .
.
Тогда, в силу (3.2)

где  . Следовательно,
. Следовательно,

В силу дифференцируемости в смысле комплексного анализа, существует предел  при
при  , а значит и предел
, а значит и предел

Таким образом, мы можем сделать вывод, что частная производная функции  по переменной
по переменной 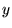 существует в точке
существует в точке  , и
, и

| (3.5) |
Объединяя (3.4) и (3.5), заключаем, что, если функция  дифференцируема в смысле комплексного анализа в точке
дифференцируема в смысле комплексного анализа в точке  , то соответствующая ей функция
, то соответствующая ей функция 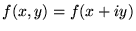 двух переменных имеет частные производные по
двух переменных имеет частные производные по  и по
и по 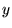 в точке
в точке  , и
, и

| (3.6) |
Равенство

| (3.7) |
называется уравнением или условием Коши-Римана.
В равенстве (3.7) выделим действительные и мнимые части. Обозначим  , тогда
, тогда

Равенство (3.7) теперь имеет вид

Приравнивая действительные и мнимые части, получим


Эти равенства также называются уравнениями Коши-Римана.
Примеры дифференцируемых и недифференцируемых функций. Отметим, что класс функций, дифференцируемых в смысле комплексного анализа, довольно узок. Самые простые функции комплексного анализа могут быть недифференцируемыми.
Пример 1. 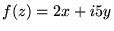 . Здесь
. Здесь

Условия Коши-Римана не выполнены, значит функция нигде не дифференцируема.
Пример 2. Проанализируем еще одну функцию с точки зрения дифференцируемости. С помощью условия Коши-Римана легко проверить, что функция 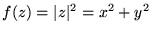 не дифференцируема при
не дифференцируема при  . По определению можно проверить, что эта функция будет все же дифференцируема в нуле. В самом деле,
. По определению можно проверить, что эта функция будет все же дифференцируема в нуле. В самом деле,

Модуль этой функции

Значит
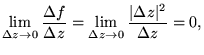
то есть производная функции  в нуле существует и равна нулю.
в нуле существует и равна нулю.
Пример 3. Пусть  , где
, где 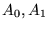 произвольные комплексные числа. Очевидно, что
произвольные комплексные числа. Очевидно, что

поэтому

Значит при любом  линейная функция
линейная функция  дифференцируема в смысле комплексного анализа и
дифференцируема в смысле комплексного анализа и

Свойства производной. Основные свойства производных вытекают из свойств пределов и доказываются так же, как и в действительном анализе.
Перечислим их: если функции  и
и  дифференцируемы в точке
дифференцируемы в точке  , то
, то
1) 
2)  (
( - комплексное число);
- комплексное число);
3) 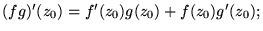

при условии, что 
5) Если  дифференцируема в точке
дифференцируема в точке  , а
, а  дифференцируема в точке
дифференцируема в точке 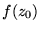 , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке  , и
, и

Пример 4. Так как функция  дифференцируема при любом
дифференцируема при любом  , то из приведенных свойств вытекает, что любой полином от
, то из приведенных свойств вытекает, что любой полином от  с комплексными коэффициентами
с комплексными коэффициентами

является дифференцируемой функцией при любом  .
.
Пример 5. Любая рациональная функция (частное двух полиномов)

дифференцируема во всех точках, где знаменатель не равен нулю, то есть во всей комплексной плоскости за исключением корней полинома  .
.
Голоморфные функции. Функция называется голоморфной в точке  области определения, если она дифференцируема в смысле комплексного анализа не только в самой точке
области определения, если она дифференцируема в смысле комплексного анализа не только в самой точке  , но и во всех точках некоторой окрестности точки
, но и во всех точках некоторой окрестности точки  .
.
Функция называется голоморфной в области, если она голоморфна во всех точках области.
Заметим, что, если функция  голоморфна в области
голоморфна в области  , и ее производная тождественно равна нулю в
, и ее производная тождественно равна нулю в  , то функция постоянна в
, то функция постоянна в  . Действительно, если
. Действительно, если  , то из равенства (3.7) следует, что частные производные функции
, то из равенства (3.7) следует, что частные производные функции 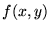 по
по  и по
и по 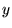 тождественно равны нулю в
тождественно равны нулю в  , следовательно, функция
, следовательно, функция 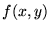 постоянна по
постоянна по  при любом
при любом 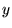 и постоянна по
и постоянна по 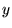 при любом
при любом  . Значит она постоянна на любой горизонтальной и вертикальной прямой в области
. Значит она постоянна на любой горизонтальной и вертикальной прямой в области  , и поэтому она будет постоянной на любой ломаной с горизонтальными и вертикальными звеньям. Но тогда она постоянна во всей области
, и поэтому она будет постоянной на любой ломаной с горизонтальными и вертикальными звеньям. Но тогда она постоянна во всей области  .
.

Из определения голоморфной функции видно, что голоморфность в области  эквивалентно тому, что всюду в области
эквивалентно тому, что всюду в области  функция имеет производную. Это следует из того, что всякая точка в области входит туда вместе с некоторой своей окрестностью, и поэтому, если функция всюду в
функция имеет производную. Это следует из того, что всякая точка в области входит туда вместе с некоторой своей окрестностью, и поэтому, если функция всюду в  имеет производную, то она будет иметь производную в некоторой окрестности каждой точки области, то есть будет голоморфна.
имеет производную, то она будет иметь производную в некоторой окрестности каждой точки области, то есть будет голоморфна.
Раз голоморфная в области функция всюду имеет производную, то она всюду в этой области непрерывна и всюду выполняются условия Коши-Римана:

при  .
.
Оказывается, что верно и обратное утверждение в следующем смысле.
Теорема (Меньшова). Если в некоторой области функция  непрерывна, всюду в области существуют частные производные
непрерывна, всюду в области существуют частные производные

и всюду в области они удовлетворяют условию Коши-Римана

то функция  дифференцируема, то есть голоморфна в данной области.
дифференцируема, то есть голоморфна в данной области.
(Доказательство этой теоремы не может быть приведено в этом курсе ввиду его сложности и объема.)
Этой теоремой можно пользоваться для практической проверки голоморфности функций, если их частные производные легко найти.
Проверим, в частности, голоморфность или, что то же дифференцируемость функции  всюду в
всюду в  и найдем ее производную. Заодно и продолжим список примеров дифференцируемых функций.
и найдем ее производную. Заодно и продолжим список примеров дифференцируемых функций.
Пример 6. Функция  всюду дифференцируема и
всюду дифференцируема и  .
.
Так как  , то
, то
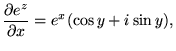
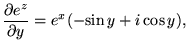
то есть частные производные, очевидно, есть всюду в  . Кроме этого можно видеть, что
. Кроме этого можно видеть, что
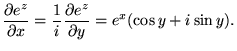
Функция  непрерывна как произведение непрерывных функций
непрерывна как произведение непрерывных функций  и
и  , зависящих только от одной переменной каждая. Значит по теореме Меньшова
, зависящих только от одной переменной каждая. Значит по теореме Меньшова  голоморфна всюду в
голоморфна всюду в  , и производная
, и производная

в силу (3.6).
Пример 7. Проверим, что тригонометрические функции  и
и 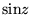 дифференцируемы всюду в комплексной плоскости и, следовательно, всюду голоморфны.
дифференцируемы всюду в комплексной плоскости и, следовательно, всюду голоморфны.
В самом деле, по определению

| (3.8) |
Функции 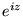 и
и 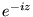 всюду дифференцируемы, поскольку они являются суперпозицией (сложной функцией) двух дифференцируемых функций:
всюду дифференцируемы, поскольку они являются суперпозицией (сложной функцией) двух дифференцируемых функций:  и линейных функций
и линейных функций  и
и  . Теперь очевидно, косинус дифференцируем, поскольку он оказывается полу суммой двух дифференцируемых функций. Аналогично синус оказывается тоже линейной комбинацией дифференцируемых функций.
. Теперь очевидно, косинус дифференцируем, поскольку он оказывается полу суммой двух дифференцируемых функций. Аналогично синус оказывается тоже линейной комбинацией дифференцируемых функций.
Используя правила дифференцирования, описанные выше, получим


Таким образом, правило дифференцирования синуса сохранилось и для комплексных переменных.
То же самое справедливо и для комплексного косинуса. В самом деле
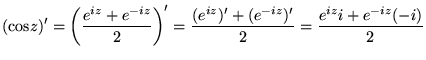

Date: 2016-01-20; view: 1906; Нарушение авторских прав