
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Коши-Гурса
|
|
Теорема (Коши-Гурса). Если функция  голоморфна в односвязной области
голоморфна в односвязной области  , то интеграл от нее по любому замкнутоиу контуру
, то интеграл от нее по любому замкнутоиу контуру 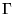 , лежащему внутри области, равен нулю
, лежащему внутри области, равен нулю

| (5.8) |

Доказательство проводится в несколько шагов.
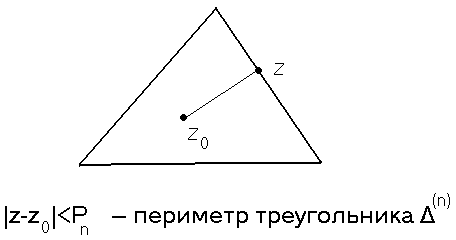
1. Рассмотрим сначала случай, когда 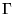 является границей треугольника, лежащего внутри
является границей треугольника, лежащего внутри  . Предположим, что для некоторого такого треугольника с границей
. Предположим, что для некоторого такого треугольника с границей 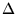
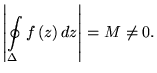
| (5.9) |
Обозначим через 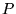 периметр этого треугольника. Разобьем треугольник на четыре равных треугольника, соединив между собой медианы его сторон.
периметр этого треугольника. Разобьем треугольник на четыре равных треугольника, соединив между собой медианы его сторон.

Интеграл по границе 
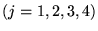 каждого треугольника можно представить как сумму интегралов по его сторонам.
каждого треугольника можно представить как сумму интегралов по его сторонам.
Если теперь сложить все интегралы, то интеграл по отрезкам, лежащим внутри исходного треугольника, уничтожаются (интегралы по ним вычисляются в двух противоположных направлениях) и останутся только интегралы по отрезкам, составляющим контур 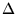 . Таким образом
. Таким образом
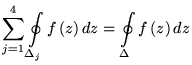
Модуль правой части равен 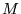 , отсюда следует, что модуль хотя бы одного слагаемого в левой части не меньше, чем
, отсюда следует, что модуль хотя бы одного слагаемого в левой части не меньше, чем  . Обозначим через
. Обозначим через 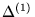 границу этого треугольника. В силу подобия его периметр будет равен
границу этого треугольника. В силу подобия его периметр будет равен 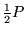 . Аналогично разбиваем этот треугольник на 4 части и, продолжая процесс, строим последовательность вложенных друг в друга треугольников с границами
. Аналогично разбиваем этот треугольник на 4 части и, продолжая процесс, строим последовательность вложенных друг в друга треугольников с границами 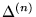 и периметрами
и периметрами 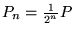 , для которых
, для которых
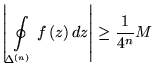
| (5.10) |
Эти треугольники имеют общую точку  . По условию функция
. По условию функция  голоморфна в этой точке, и ее можно представить в виде
голоморфна в этой точке, и ее можно представить в виде
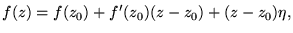
где 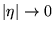 , когда
, когда 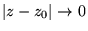 . Вычисляем
. Вычисляем

в (5.2) и (5.3) было показано что  и
и  , поэтому
, поэтому
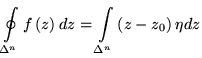
воспользуемся оценкой интеграла (5.5) и тем что  , тогда
, тогда
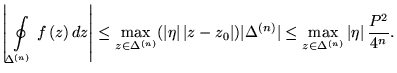
| (5.11) |
Сравнивая равенства (5.10) и (5.11), сокращая на 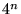 , получаем
, получаем
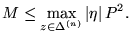
Когда  увеличивается, граница
увеличивается, граница 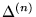 стягивается к точке
стягивается к точке  и поэтому
и поэтому 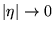 , что противоречит последнему неравенству. Итак, предположение (5.9) привело нас к противоречию, и, следовательно, интеграл по границе любого треугольника, лежащего в
, что противоречит последнему неравенству. Итак, предположение (5.9) привело нас к противоречию, и, следовательно, интеграл по границе любого треугольника, лежащего в  , равен нулю.
, равен нулю.

2. Рассмотрим теперь интеграл по границе любого многоугольника, лежащего в  . Этот многоугольник можно разбить на несколько треугольников. Тогда интеграл по границе многоугольника будет равняться сумме интегралов по границам треугольников (интегралы по внутренним разрезам взаимно уничтожаются) и, так как интегралы по границам треугольников равны 0, то и интеграл по границе многоугольника равен нулю.
. Этот многоугольник можно разбить на несколько треугольников. Тогда интеграл по границе многоугольника будет равняться сумме интегралов по границам треугольников (интегралы по внутренним разрезам взаимно уничтожаются) и, так как интегралы по границам треугольников равны 0, то и интеграл по границе многоугольника равен нулю.
Пусть теперь 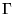 - замкнутая кусочно-гладкая жорданова кривая, лежащая в
- замкнутая кусочно-гладкая жорданова кривая, лежащая в  . Как показано в параграфе 3 интеграл по этой кривой можно с любой точностью приблизить интегралом по ломанной. Эта ломанная будет границей многоугольника, который в силу односвязности области
. Как показано в параграфе 3 интеграл по этой кривой можно с любой точностью приблизить интегралом по ломанной. Эта ломанная будет границей многоугольника, который в силу односвязности области  будет лежать в
будет лежать в  и, следовательно, интеграл по его границе будет равен нулю. Число, которое можно с любой точностью приблизить нулем, само равно нулю.
и, следовательно, интеграл по его границе будет равен нулю. Число, которое можно с любой точностью приблизить нулем, само равно нулю.
Теорема Коши-Гурса доказана.
Теорема о составом контуре. Рассмотрим подробнее двухсвязную область  , ограниченную двумя кусочно- гладкими жордановыми кривыми (область с дырой) и функцию
, ограниченную двумя кусочно- гладкими жордановыми кривыми (область с дырой) и функцию  голоморфную в
голоморфную в  . Если контур
. Если контур 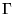 не содержит внутри себя дыру, то в силу теоремы Коши-Гурса интеграл по нему равен нулю. Поэтому интересно исследовать интегралы по контурам, содержащим дыру внутри.
не содержит внутри себя дыру, то в силу теоремы Коши-Гурса интеграл по нему равен нулю. Поэтому интересно исследовать интегралы по контурам, содержащим дыру внутри.
Пусть 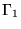 и
и  два таких контура, причем
два таких контура, причем 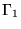 лежит внутри
лежит внутри  . Направления на контурах
. Направления на контурах 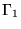 и
и  выбраны так, что при движении по этим направлениям дыра остается слева. Криволинейное кольцо ограниченное кривыми
выбраны так, что при движении по этим направлениям дыра остается слева. Криволинейное кольцо ограниченное кривыми 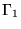 и
и  разобьем на два полукольца с помощью двух разрезов
разобьем на два полукольца с помощью двух разрезов  и
и  (см. рисунок). Направление на разрезе выберем так, чтобы начало лежало на
(см. рисунок). Направление на разрезе выберем так, чтобы начало лежало на  , а конец на
, а конец на 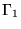 . Эти точки делят кривые
. Эти точки делят кривые 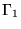 и
и  на части
на части  и
и 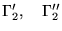 . Составим теперь два замкнутых контура
. Составим теперь два замкнутых контура 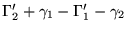 и
и 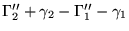 , где знак ``-'' означает, что на кривой направление изменено на противоположное. Эти контуры не содержат внутри себя дыру и поэтому интегралы по ним в силу теоремы Коши-Гурса равны нулю. Пользуясь свойствами интеграла, каждый из указанных интегралов можно представить как сумму интегралов по четырем частям.
, где знак ``-'' означает, что на кривой направление изменено на противоположное. Эти контуры не содержат внутри себя дыру и поэтому интегралы по ним в силу теоремы Коши-Гурса равны нулю. Пользуясь свойствами интеграла, каждый из указанных интегралов можно представить как сумму интегралов по четырем частям.

Тогда
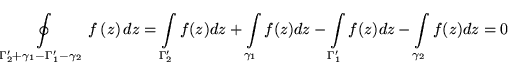

При сложении этих равенств интегралы по  и
и  взаимно уничтожаются, а интегралы по
взаимно уничтожаются, а интегралы по 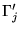 и
и 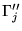 в сумме дают интеграл по
в сумме дают интеграл по  .
.
Таким образом,

| (5.12) |
и, следовательно, интеграл не изменяется при переходе от одного контура к другому.
Пример. Пусть точка 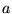 внутри контура
внутри контура 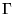 , тогда
, тогда
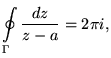
где направление интегрирования берется против часовой стрелки.
Действительно, для окружности этот интеграл вычислен, так как функция голоморфна при  неравном
неравном 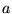 , то он будет таким же и для контура
, то он будет таким же и для контура 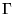 .
.
Доказанное свойство (5.12), как это видно уже на примере, позволяет сводить задачу вычисления интегралов по замкнутым контурам сложной природы к вычислению интегралов по более простым контурам и является мощным средством для вычисления интегралов.
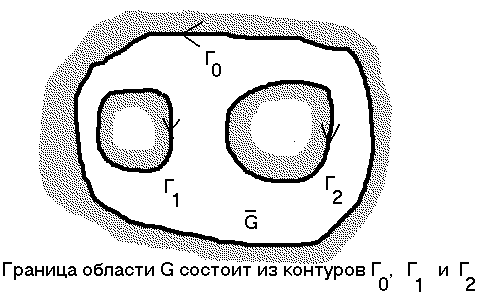
Сформулируем теперь следствие из теоремы Коши-Гурса для многосвязной области, то есть области с большим количеством "дыр". Пусть  ограниченная область, граница которой состоит из конечного числа кусочно-гладких замкнутых жордановых кривых, и пусть функция
ограниченная область, граница которой состоит из конечного числа кусочно-гладких замкнутых жордановых кривых, и пусть функция  , определенна на замыкании
, определенна на замыкании 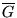 , непрерывна в
, непрерывна в 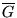 и голоморфна в
и голоморфна в  . Тогда сумма интегралов от этой функции по всем граничным кривым равна нулю, если направление обхода кривых выбрать, например, так, чтобы при обходе область
. Тогда сумма интегралов от этой функции по всем граничным кривым равна нулю, если направление обхода кривых выбрать, например, так, чтобы при обходе область  оставалась слева.
оставалась слева.
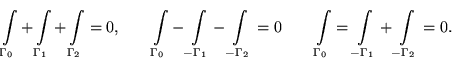
Иными словами интеграл по внешнему контуру  равен сумме интегралов по внутренним контурам
равен сумме интегралов по внутренним контурам 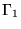 и
и  , если во всех случаях берется интеграл по направлению против часовой стрелки и между контурами подинтегральная функция голоморфна. Разумеется аналогичное утверждение справедливо и для большего числа чем два внутренних контуров.
, если во всех случаях берется интеграл по направлению против часовой стрелки и между контурами подинтегральная функция голоморфна. Разумеется аналогичное утверждение справедливо и для большего числа чем два внутренних контуров.
Независимость интеграла от вида пути интегрирования. Пусть функция  голоморфна в односвязной области
голоморфна в односвязной области  . Возьмем две точки
. Возьмем две точки 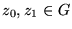 и соединим их двумя различными кусочно-гладкими простыми кривыми
и соединим их двумя различными кусочно-гладкими простыми кривыми  и
и 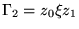 . Из этих кривых можно составить замкнутый контур
. Из этих кривых можно составить замкнутый контур  .
.
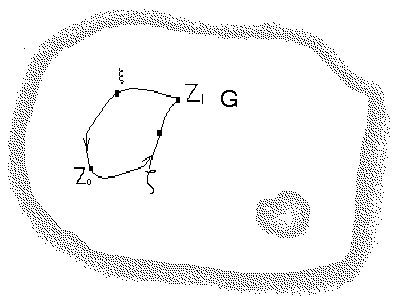
По теореме Коши-Гурса

разбиваем интеграл в сумму двух


отсюда

Следовательно, интеграл от голоморфной в односвязной области функции не зависит от вида пути интегрирования, а зависит только от положения его начала и конца.
В условиях, когда интеграл не зависит от вида пути интегрирования его можно обозначать так
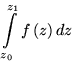
Первообразная функция. Как и в обычном анализе первообразной функцией от данной функции называется функция, производная которой равна данной функции.
По определению для первообразной функции  мы имеем
мы имеем  . Следовательно, если функция
. Следовательно, если функция  имеет в области
имеет в области  первообразную, то эта первообразная дифференцируема в области и поэтому первообразная голоморфна.
первообразную, то эта первообразная дифференцируема в области и поэтому первообразная голоморфна.
Две первообразные от одной и той же функции отличаются на постоянное слагаемое. Действительно, если 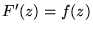 и
и  ,
,  , то
, то  . Отсюда следует, что
. Отсюда следует, что 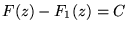 или
или 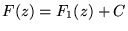 .
.
Лемма о существовании первообразной. Если функция  непрерывна в области
непрерывна в области  и интеграл от нее не зависит от вида пути интегрирования, то она имеет в этой области первообразную.
и интеграл от нее не зависит от вида пути интегрирования, то она имеет в этой области первообразную.
Доказательство. Зафиксируем точку  и введем функцию
и введем функцию
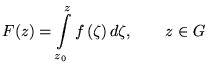
| (5.13) |
Покажем, что она как раз и является искомой первообразной. Вычисляем




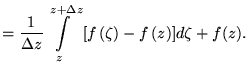
Оценим интеграла справа. Поскольку интеграл по условию не зависит от вида пути интегрирования, то можно считать, что часть кривой, соединяющая точки  и
и  , является отрезком
, является отрезком  прямой, тогда
прямой, тогда

В силу непрерывности функции  правая часть стремится к нулю, когда
правая часть стремится к нулю, когда 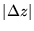 стремится к нулю. Таким образом,
стремится к нулю. Таким образом,

Лемма доказана.
Если функция  голоморфна в односвязной области, то она по интегральной теореме Коши-Гурса удовлетворяет всем условиям леммы. Таким образом, справедливо
голоморфна в односвязной области, то она по интегральной теореме Коши-Гурса удовлетворяет всем условиям леммы. Таким образом, справедливо
Следствие. Если функция голоморфна в односвязной области, то она имеет в этой области первообразную.
Формула Ньютона-Лейбница. Пусть 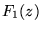 - первообразная от голоморфной в односвязной области
- первообразная от голоморфной в односвязной области  функции
функции  . Из доказательства леммы следует, что функция
. Из доказательства леммы следует, что функция  из (5.13) также является первообразной от
из (5.13) также является первообразной от  . Тогда функции
. Тогда функции  и
и 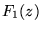 отличаются на константу, то есть
отличаются на константу, то есть

Значит

или

6. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ
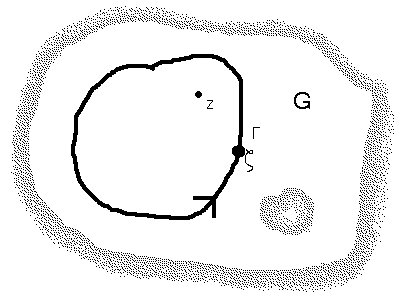
Формула Коши. Пусть в области G задана функция f(z), голоморфная в G. Рассмотрим кусочно-гладкую простую замкнутую кривую (жорданов контур)  такой, что внутренность
такой, что внутренность 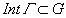 .
.
Введем в рассмотрение функцию 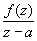 , где
, где  . Эта функция будет всюду в G голоморфной, за исключением точки a.
. Эта функция будет всюду в G голоморфной, за исключением точки a.
Построим окружность  центром в точке
центром в точке  радиуса
радиуса  , лежащую внутри
, лежащую внутри  .
.

Как следует из теоремы о составном контуре
 ,
,
так как функция 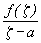 – голоморфна между контурами Г и
– голоморфна между контурами Г и  .
.
Добавим и отнимем 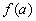 в числителе последнего интеграла. Тогда
в числителе последнего интеграла. Тогда
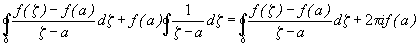
так как

Оценим интеграл,
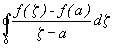
учтя то, что на окружности 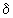 мы имеем
мы имеем  ,
,

В силу непрерывности функции f(z)
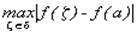 ,
,
а значит и
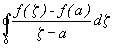
стремятся к нулю при  . Переходя к пределу при
. Переходя к пределу при  в
в

получаем:
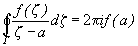
или
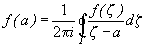 (6.1)
(6.1)
при  .
.
Это равенство и называется интегральной формулой Коши. Формула Коши обладает, по крайней мере, двумя свойствами. Во-первых, она позволяет вычислить значение голоморфной функции внутри области, зная ее значения на границе области. Во-вторых, если ее записать так
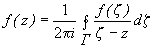 ,
,
и вспомнить, что интеграл есть предел интегральных сумм, то из формулы будет следовать, что функция f(z) может быть представлена как предел линейных комбинаций простейших функций  . Оба эти качества формулы Коши широко используются.
. Оба эти качества формулы Коши широко используются.
Заметим, что если точка a лежит вне контура Г, то есть 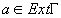 ,то внутри Г функция
,то внутри Г функция 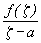 будет голоморфна. По теореме Коши-Гурса интеграл от нее по Г равен 0. Таким образом, если заменить a на z, то получаем:
будет голоморфна. По теореме Коши-Гурса интеграл от нее по Г равен 0. Таким образом, если заменить a на z, то получаем:
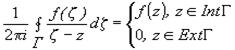 (6.2)
(6.2)
Date: 2016-01-20; view: 3774; Нарушение авторских прав