Формула Тейлора

Пусть функция голоморфна в точке . Тогда она голоморфна и в некоторой окрестности точки 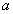. Окружим эту точку контуром Г, лежащим в указанной окрестности.

Внутреннюю область, ограниченную Г, обозначим через U.

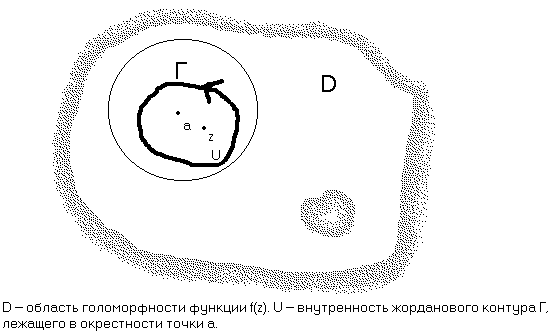
Запишем интегральную формулу Коши

при .

Преобразуем

Воспользуемся формулой для суммы геометрической прогрессии

.

Отсюда

.

Применим последнюю формулу, полагая 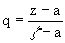. Тогда

.

Воспользуемся формулами (6.6) из §6 для производных, тогда получим формулу Тейлора

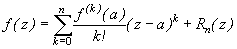
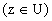, (7.1)

в которой остаточный член

. (7.2)

Функция является непрерывной на Г, поэтому

.

будет интегралом типа Коши, построенным для этой функции, и, следовательно, функция 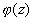– голоморфна внутри Г. При этом

.

Формулу Тейлора можно записать в виде

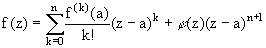. (7.3)

где функция 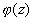голоморфна в U. При этом

(7.4)

в силу формулы Коши для производных.

Оценка остатка формулы Тейлора. Рассмотрим произвольную голоморфную функцию 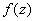в области D. Пусть . Напишем формулу Тейлора для функции в точке .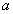

.

Оценим функцию –остаток в формуле Тейлора в такой круговой окрестности точки 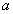, которая целиком вписывается в область D.

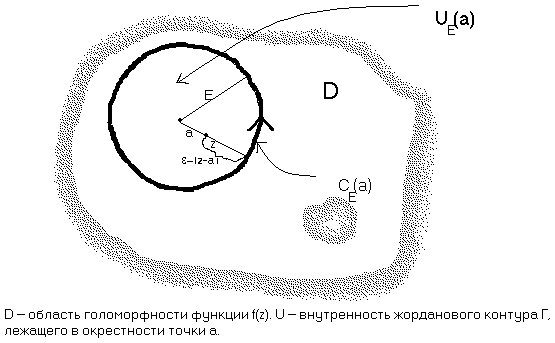
Пусть - это круг радиуса с центром в точке 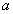, который вместе со своей границей, окружностью , лежит в области .

Наша цель – оценить при . Для этого мы применим формулу (6.2) из предыдущего параграфа, взяв в качестве контура Г окружность .

Тогда получим

Обозначим через , тогда мы можем оценить максимум числителя, и получить продолжение предыдущей оценки, учитывая, что ,

= .

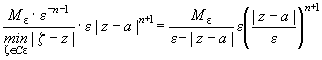Таким образом,

,

Это и есть нужная нам оценка остаточного члена в формуле Тейлора. Принципиально важным является то, что остаточный член довольно быстро стремится к нулю при росте . В самом деле, при по определению , и поэтому . Это значит, что остаточный член по модулю оказывается не превосходит убывающей геометрической прогрессии. То есть при мы получим 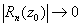, т.к. .

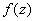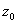Теорема Тейлора для голоморфных функций. Как прежде предположим, что функция – голоморфна в области . Пусть , и рассмотрим произвольный открытый круг с центром в точке , который целиком вписывается в область . Обозначим его радиус через .

Теорема (Тейлора). Для любого из круга , справедливо равенство

.

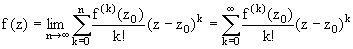Доказательство. Пусть . Рассмотрим замкнутый круг радиуса с центром в точке 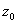, который с одной стороны содержит точку внутри, то есть , а с другой стороны пусть .

Оценим теперь разность между 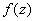и суммой , опираясь на оценку остаточного члена в формуле Тейлора

.

Тогда при имеем 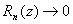, или .

Теорема доказана.

Выражение вида называется рядом Тейлора функции 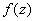с центром в точке .

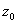Таким образом, утверждение теоремы Тейлора состоит в том, что в любом круге с центром в точке 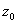, который вписывается в область голоморфности функции 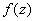, эта голоморфная функция совпадает со своим рядом Тейлора с центром в точке .

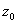Теорему Тейлора еще можно сформулировать и так. Если функция 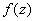голоморфна в круге , то всюду в этом круге, то есть при справедливо равенство

.

Date: 2016-01-20; view: 590; Нарушение авторских прав