Функции комплексного переменного

Функции комплексного переменного. Говорят, что на множестве 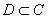комплексных чисел определена функция, если каждому числу 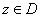поставлено в соответствие комплексное число 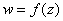. Если положить 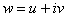, то функцию можно записать в виде 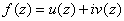. Таким образом, функция задается парой функций, определенных на 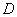и принимающих действительные значения. Если положить 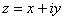, то функцию можно записать в виде 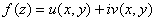, и, значит, функция может быть задана парой действительных функций двух действительных переменных.

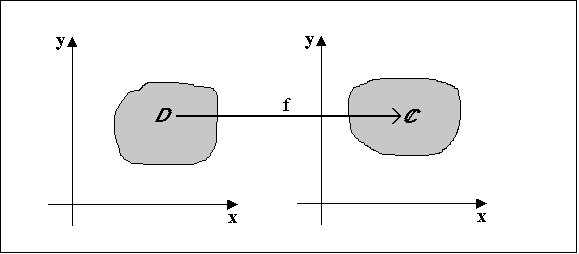
Комплексная линейная функция. Простейшей является линейная функция

,

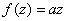где 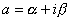- комплексное число, неравное нулю. Чтобы найти соответствующую пару действительных функций, расписываем

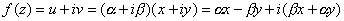
Откуда

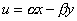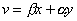, (2.1)

Таким образом, возникает пара линейных функций двух переменных, однако, не произвольных, а связанных между собой. Систему (2.1) можно рассматривать как линейное отображение плоскости 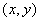на плоскость 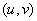, задаваемое матрицей

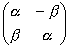, то есть .

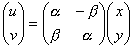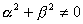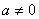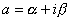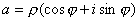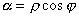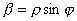Определитель матрицы равен , так как и, следовательно, она обратима. Для выяснения геометрических свойств полученного отображения воспользуемся тригонометрической формой числа , то есть пусть . Тогда и , и

.

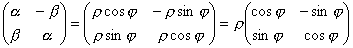Как известно, матрица справа определяет поворот плоскости вокруг начала координат на угол 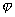, а умножение на положительное число дает растяжение плоскости. При этом 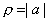, а 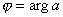. При указанных преобразованиях сохраняются углы между векторами на плоскости. Такие преобразования называются линейными конформными. Итак, линейная функция комплексного переменного порождает конформное линейное отображение комплексной плоскости.

Рассмотрим теперь функцию 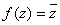. Здесь 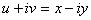, т.е. 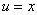, 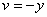. Эти равенства порождают отображение симметрии относительно действительной оси.

Показательная функция комплексного переменного. По определению полагают

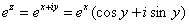. (2.2)

Очевидно, что при 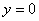будет 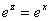. Таким образом показательная функция является продолжением вещественной показательной функции на всю комплексную плоскость.

Выделим ее действительную и мнимую части

,

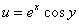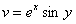
модуль и аргумент, то есть и .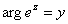

Date: 2016-01-20; view: 502; Нарушение авторских прав