
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Т а б л и ц а 65
|
|
Стоимость репетиторских услуг по математике
| Год | Период | Цена занятия, р. | Год | Период | Цена занятия, р. |

Рис. 46. Динамика стоимости репетиторских услуг
Решение в Excel
1. Ввод исходных данных и оформление их в виде таблицы, удобной для расчета оценок сезонной компоненты.
2. Расчет оценок сезонной компоненты для мультипликативной модели.
2.1. Расчет скользящих средних с периодом усреднения, равным четырем.
2.2. Вычисление сезонной компоненты в виде частного от деления фактических уровней временного ряда на значения центрированных скользящих средних.
2.3. Оформление результатов расчетов в виде табл. 66.
Т а б л и ц а 66
Расчет оценок сезонной компоненты в мультипликативной модели
| Год | Период | Фактические данные | Скользящая средняя | Оценка сезонной компоненты |
| – | – | |||
| – | – | |||
| 120,0 | 1,08 | |||
| 130,0 | 1,38 | |||
| 145,0 | 0,76 | |||
| 160,0 | 1,00 | |||
| 177,5 | 1,07 | |||
| 185,0 | 1,35 | |||
| 195,0 | 0,72 | |||
| 212,5 | 0,94 | |||
| 225,0 | 1,16 | |||
| 235,0 | 1,28 | |||
| 240,0 | 0,75 | |||
| 250,0 | 0,88 | |||
| 267,5 | 1,12 | |||
| 272,5 | 1,36 | |||
| 282,5 | 0,71 | |||
| 295,0 | 0,88 | |||
| 310,0 | 1,13 | |||
| 315,0 | 1,37 | |||
| 322,5 | 0,68 | |||
| 337,5 | 0,86 | |||
| 347,5 | 1,18 | |||
| – | – |
3. Расчет средних значений сезонной компоненты мультипликативной модели.
3.1. Формирование из оценок сезонной компоненты, полученных в предыдущем пункте, табл. 67, удобной для расчета средних значений этой же компоненты.
3.2. Расчет итоговых значений сезонной компоненты.
3.3. Определение средних значений итоговой компоненты.
3.4. Определение корректирующего коэффициента

 .
.
3.5. Расчет скорректированных значений сезонной компоненты путем умножения корректирующего коэффициента из средних оценок сезонной компоненты (сумма скорректированных значений равна четырем).
4. Вычисление основных составляющих сезонной модели.
4.1. Элиминирование влияния сезонной компоненты путем деления каждого уровня исходного временного ряда на соответствующие значения сезонной составляющей.
4.2. Построение по данным элиминированного временного ряда трендовой модели с помощью МНК (см. Вывод итогов 16).
Т а б л и ц а 67
Расчет сезонной компоненты в мультипликативной модели
| Показатель | Год | Период | |||
| – | – | 1,08 | 1,38 | ||
| 0,76 | 1,00 | 1,07 | 1,35 | ||
| 0,72 | 0,94 | 1,16 | 1,28 | ||
| 0,75 | 0,88 | 1,12 | 1,36 | ||
| 0,71 | 0,88 | 1,13 | 1,37 | ||
| 0,68 | 0,86 | 1,18 | – | ||
| Итого за период (за все годы) | 3,62 | 4,56 | 6,74 | 6,74 | |
| Средняя оценка сезонной компоненты | 0,72 | 0,91 | 1,12 | 1,35 | |
| Скорректированная сезонная компонента | 0,70 | 0,89 | 1,09 | 1,31 |
| ВЫВОД ИТОГОВ 16 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,990535 | |||||
| R-квадрат | 0,98116 | |||||
| Нормированный R-квадрат | 0,980303 | |||||
| Стандартная ошибка | 11,23861 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 144709,3 | 144709,3 | 1145,701 | 1,8E-20 | ||
| Остаток | 2778,74 | 126,3064 | ||||
| Итого | 147488,1 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 97,792 | 4,735394 | 20,65129 | 6,81E-16 | 87,97139 | 107,6126 |
| Переменная X 1 | 11,21758 | 0,331409 | 33,84821 | 1,8E-20 | 10,53028 | 11,90488 |
4.3. Получение расчетных значений по трендовой модели
 .
.
4.4. Расчет значений уровня ряда по мультипликативной модели.
4.5. Оформление результатов расчетов в виде табл. 68.
Т а б л и ц а 68
Расчетные значения мультипликативной тренд-сезонной модели

| Цена
занятия,

| Сезонная
компонента,

| Десезонализи-
рованная цена,

| Расчетные значения
(линейный тренд)

| Расчетные
значения цены

|
| 0,70 | 99,34 | 109,01 |
Окончание табл. 68
| 0,89 | 112,51 | 120,23 | |||
| 1,09 | 118,80 | 131,44 | |||
| 1,31 | 137,16 | 142,66 | |||
| 0,70 | 156,10 | 153,88 | |||
| 0,89 | 180,02 | 165,10 | |||
| 1,09 | 173,63 | 176,32 | |||
| 1,31 | 190,51 | 187,53 | |||
| 0,70 | 198,68 | 198,75 | |||
| 0,89 | 225,03 | 209,97 | |||
| 1,09 | 237,60 | 221,19 | |||
| 1,31 | 228,61 | 232,40 | |||
| 0,70 | 255,44 | 243,62 | |||
| 0,89 | 247,53 | 254,84 | |||
| 1,09 | 274,16 | 266,06 | |||
| 1,31 | 281,95 | 277,27 | |||
| 0,70 | 283,83 | 288,49 | |||
| 0,89 | 292,53 | 299,71 | |||
| 1,09 | 319,85 | 310,93 | |||
| 1,31 | 327,67 | 322,14 | |||
| 0,70 | 312,21 | 333,36 | |||
| 0,89 | 326,29 | 344,58 | |||
| 1,09 | 374,68 | 355,80 | |||
| 1,31 | 358,15 | 367,01 |
5. Оценка качества построенной модели.
5.1. Расчет суммы квадратов отклонений фактических значений цены занятия от среднего значения.
5.2. Расчет суммы квадратов отклонений расчетных от фактических значений цены занятия.
5.3. Оформление результатов расчетов в виде табл. 69.
Т а б л и ц а 69
Расчет квадратов отклонений

| 
| 
| 
| 
| 
| 
| 
|
| 46,43 | 29326,56 | 42,22 | 451,56 | ||||
| 47,01 | 19951,56 | 78,58 | 3451,56 | ||||
| 191,42 | 12376,56 | 37,66 | 16576,56 | ||||
| 52,05 | 3751,56 | 10,80 | 1701,56 | ||||
| 2,46 | 17226,56 | 40,68 | 351,56 | ||||
| 175,91 | 6601,56 | 95,34 | 11826,56 | ||||
| 8,62 | 2626,56 | 52,62 | 35626,56 | ||||
| 15,23 | 76,56 | 222,15 | 451,56 | ||||
| 0,00 | 10251,56 | 264,33 | 2376,56 | ||||
| 179,10 | 1701,56 | 427,01 | 28476,56 | ||||
| 322,72 | 351,56 | 135,23 | 52326,56 | ||||
| 24,80 | 3451,56 | Суммы | |||||
| 69,41 | 3751,56 | 2541,79 | 265062,50 |
5.4. Расчет величины по формуле
 .
.
Таким образом, мультипликативная модель объясняет 99 % общей вариации уровней временного ряда стоимости репетиторских услуг за рассматриваемый промежуток времени.
6. Расчет прогнозных значений для каждого сезонного периода 2006 г. и оформление результатов расчетов в виде табл. 70.
Т а б л и ц а 70
Прогнозирование стоимости репетиторских услуг
| Год | Период | Прогнозные значения тренда | Сезонная компонента | Прогнозные значения цены |
| Август-октябрь | 378,23 | 0,70 | ||
| Ноябрь-декабрь | 389,45 | 0,89 | ||
| Январь-март | 400,67 | 1,09 | ||
| Апрель-июль | 411,88 | 1,31 |
7. Построение графика (см. рис. 47) стоимости репетиторских услуг в г. Воронеже (фактических, рассчитанных по трендовой и мультипликативной моделям).

Рис. 47. Динамика фактической и расчетной цены занятия
8. Решение в STATISTICA аналогично решению примера 15. Только в окне Seasonal Decomposition (Census 1)/Advance – Сезонная декомпозиция/ Дополнительно необходимо сделать показанные на рис. 48 установки: Seasonal model –Multiplicative (Сезонная модель – мультипликативная); Seasonal lag (Сезонный лаг, т.е. длина сезонного периода) – 4; Number of backups per variable (Число дублирований каждой переменной) – 6.

Рис. 48. Окно Seasonal Decomposition (Census 1) – Сезонная декомпозиция
Пример 17. Аграрный комитет администрации Воронежской области, зная среднегодовой спрос на молоко населения области, заинтересован в получении прогнозных оценок производства этого продукта хозяйствами всех категорий на следующий год. Такая информация ему необходима для того, чтобы иметь представление о степени обеспеченности населения молочной продукцией, и в случае существенного превышения спроса над предложением молока ориентировать торговые организации на заключение договоров поставки молока с производителями из других регионов. Построение прогнозной модели требуется осуществить по данным табл. 71.
Т а б л и ц а 71
Производство молока в хозяйствах всех категорий Воронежской обл., т.
| Год | 1-й квартал | 2-й квартал | 3-й квартал | 4-й квартал |
Решение с помощью MS Excel
1. Ввод исходных данных и оформление их в удобном для проведения расчетов виде.
2. Формирование фиктивных переменных  :
:
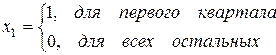 ;
;
 ;
;
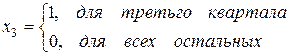 .
.
и оформление полученных результатов в виде табл. 72.
Т а б л и ц а 72
Данные для построения модели с фиктивными переменными

| 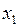
| 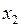
| 
| 
| 
| 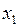
| 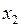
| 
| 
|
3. Оценка параметров модели
 ,
,
обычным МНК с помощью «Пакета анализа» (см. Вывод итогов 17).
Таким образом, построенная модель имеет вид
 .
.
Коэффициент корреляции достаточно высокий, что свидетельствует о существовании тесной взаимосвязи объема молока от соответствующих факторов.
Сравнение  с табличным значением дисперсионного отношения Фишера
с табличным значением дисперсионного отношения Фишера  позволяет сделать вывод об адекватности построенной модели.
позволяет сделать вывод об адекватности построенной модели.
Сравнение расчетных значений  -статистик с табличным значением
-статистик с табличным значением  говорит о том, что включенные в модель факторы значимы, кроме фактора времени. Таким образом, тенденция уменьшения объема молока существует, но она статистически незначима на 5%-м уровне значимости. Поэтому необходимо перестроить модель, исключив из нее незначимый фактор.
говорит о том, что включенные в модель факторы значимы, кроме фактора времени. Таким образом, тенденция уменьшения объема молока существует, но она статистически незначима на 5%-м уровне значимости. Поэтому необходимо перестроить модель, исключив из нее незначимый фактор.
| ВЫВОД ИТОГОВ 17 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,996532 | |||||
| R-квадрат | 0,993076 | |||||
| Нормированный R-квадрат | 0,991618 | |||||
| Стандартная ошибка | 238,7258 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1,55E+08 | 681,225 | 3,18E-20 | |||
| Остаток | 56990,02 | |||||
| Итого | 1,56E+08 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значе-ние | Нижние 95% | Верхние 95% | |
| Y-пересечение | 5576,383 | 139,5406 | 39,96243 | 8,46E-20 | 5284,321 | 5868,445 |
| Переменная X 1 | -7,50357 | 7,133298 | -1,05191 | 0,306037 | -22,4337 | 7,426598 |
| Переменная X 2 | 497,9893 | 139,4798 | 3,570331 | 0,002042 | 206,0545 | 789,9241 |
| Переменная X 3 | 5498,493 | 138,5648 | 39,68174 | 9,65E-20 | 5208,473 | 5788,512 |
| Переменная X 4 | 5131,83 | 138,0129 | 37,1837 | 3,27E-19 | 4842,965 | 5420,694 |
4. Оценка параметров модели

обычным МНК с помощью «Пакета анализа» (см. Вывод итогов 18).
| ВЫВОД ИТОГОВ 18 | |||||||||||||
| Регрессионная статистика | |||||||||||||
| Множественный R | 0,996329 | ||||||||||||
| R-квадрат | 0,992672 | ||||||||||||
| Нормированный R-квадрат | 0,991573 | ||||||||||||
| Стандартная ошибка | 239,3606 | ||||||||||||
| Наблюдения | |||||||||||||
| Дисперсионный анализ | |||||||||||||
| df | SS | MS | F | Значимость F | |||||||||
| Регрессия | 1,55E+08 | 903,1216 | 1,65E-21 | ||||||||||
| Остаток | 57293,52 | ||||||||||||
| Итого | 1,56E+08 | ||||||||||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Зна-чение | Нижние 95% | Верхние 95% | ||||||||
| Y-пересечение | 5471,33 | 97,71857 | 55,99072 | 1,85E-23 | 5267,496 | 5675,171 | |||||||
| Переменная X 1 | 520,5 | 138,1949 | 3,766419 | 0,001214 | 232,2306 | 808,7694 | |||||||
| Переменная X 2 | 5513,5 | 138,1949 | 39,89654 | 1,53E-20 | 5225,231 | 5801,769 | |||||||
| Переменная X 3 | 5139,33 | 138,1949 | 37,18901 | 6,14E-20 | 4851,064 | 5427,603 | |||||||
Следовательно, построенная модель имеет вид
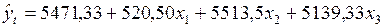 .
.
Анализ этой модели позволяет сделать вывод о ее пригодности для целей прогнозирования.
5. Получение с помощью построенной модели прогнозных оценок производства молока на 2004 год и оформление результатов в виде табл. 73.
Т а б л и ц а 73
Прогнозные оценки производства молока, т.
| Год | Квартал | 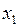
| 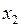
| 
| 
|
| 5991,83 | |||||
| 10984,83 | |||||
| 10610,67 | |||||
| 5471,33 |
6. Построение графика, отражающего фактическую и прогнозную динамику производства молока (см. рис. 49).
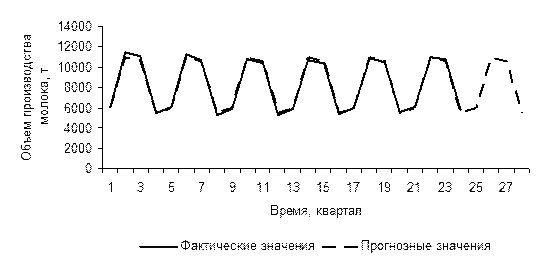
Рис. 49. Прогнозная динамика производства молока
Замечание: Решение рассмотренной задачи в STATISTICA предполагает построение модели множественной регрессии.
Пример 18. Рассмотрим прогностические возможности адаптивной модели с линейным трендом и аддитивной сезонной компонентой на примере моделирования потребления мороженого (см. табл. 74, рис. 50).
Т а б л и ц а 74
Потребление мороженого в г. Воронеже (тыс. р)
| С е з о н | Г о д | ||||
| Зима | 253,1 | 265,5 | 277,9 | 290,3 | 301,3 |
| Весна | 331,2 | 343,6 | 356,0 | 368,4 | 375,4 |
| Лето | 364,3 | 376,7 | 389,1 | 401,5 | 412,4 |
| Осень | 292,4 | 304,8 | 317,2 | 343,2 | 337,5 |

Рис. 50. Динамика потребления мороженого
Решение в Excel
1. Ввод исходных данных.
2. Деление множества наблюдений на три части: первые восемь наблюдений будем использовать для построения линейного тренда и выделения сезонной составляющей; следующие восемь наблюдений – для настройки параметров адаптации; оставшиеся четыре будут использованы в качестве контрольной выборки.
3. Построение (с использованием обычного МНК) по первым восьми наблюдениям трендовой модели  , параметры которой принимаются за начальные значения
, параметры которой принимаются за начальные значения  и
и  .
.
4. Вычисление расчетных значений

5. Определение отклонения тренда от фактических значений

6. Получение оценок сезонных составляющих как усредненных значений соответствующих отклонений
 ;
;
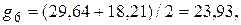
 ;
;
 .
.
7. Выбор начальных значений параметров адаптации  ,
,  ,
, 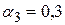 .
.
8. Осуществление адаптивной настройки параметров модели.
8.1. Расчет при заданных начальных значениях  ,
,  на данных обучающей выборки (с 9-го по 12-е наблюдение) текущих значений коэффициентов тренда и сезонной составляющей
на данных обучающей выборки (с 9-го по 12-е наблюдение) текущих значений коэффициентов тренда и сезонной составляющей

8.2. Проведение постпрогнозных расчетов для 13 – 16 наблюдений и вычисление относительных ошибок

8.3. Подбор параметров адаптации таким образом, чтобы максимальная относительная ошибка была минимальной. Минимальное значение максимальной относительной ошибки  получено при
получено при  ,
,  ,
, 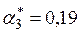 .
.
8.4. Оформление результатов всех расчетов в виде табл. 75.
Таким образом, модель для прогнозирования потребления мороженого в окончательном виде может быть записана следующим образом:
 ,
,
где 
9. Расчет прогнозных оценок и сравнение их с данными контрольной выборки

Результаты расчетов свидетельствует о том, что с помощью построенной модели удается осуществить достаточно точную экстраполяцию динамики потребления мороженого.
Т а б л и ц а 75
Результаты моделирования потребления мороженого

| 
| 
| 
| 
| 
| 
| |
| Данные для построения линейного тренда | 253,1 | 295,60 | -42,50 | ||||
| 331,2 | 301,56 | 29,64 | |||||
| 364,3 | 307,51 | 56,79 | |||||
| 292,4 | 313,47 | -21,07 | |||||
| 265,5 | 319,43 | -53,93 | -48,21 | ||||
| 343,6 | 325,39 | 18,21 | 23,93 | ||||
| 376,7 | 331,34 | 45,36 | 51,07 | ||||
| 304,8 | 337,30 | -32,50 | -26,79 | ||||
| Данные для настройки параметров адаптации | 277,9 | -43,00 | 298,65 | 6,72 | |||
| 28,49 | 308,04 | 7,39 | |||||
| 389,1 | 
| 54,94 | 317,69 | 7,95 | |||
| 317,2 | -23,65 | 327,48 | 8,41 | ||||
| 290,3 | 292,8906 | -0,89 | -38,22 | 308,16 | 1,48 | ||
| 368,4 | 372,7923 | -1,19 | 33,67 | 312,67 | 2,24 | ||
| 401,5 | 407,6451 | -1,53 | 60,35 | 318,07 | 3,03 | ||
| 343,2 | 337,4714 | 1,67 | -15,83 | 325,68 | 4,17 | ||
| Контрольная выборка | 301,3 | 291,6268 | 3,21 | ||||
| 375,4 | 367,689 | 2,05 | |||||
| 412,4 | 398,5413 | 3,36 | |||||
| 337,5 | 326,538 | 3,25 |
Пример 19. Требуется построить адаптивную модель с линейным трендом и мультипликативной компонентой сезонности для прогнозирования прибыли компании «Восход». Условные данные для расчетов приведены в табл. 76. Динамика прибыли компании отражена на рис. 51.
Т а б л и ц а 76
Прибыль компании «Восход», тыс. долл. США
| Год | Квартал | Прибыль | Год | Квартал | Прибыль |
По аналогии с предыдущими примерами разделим множество наблюдений на три части: первые восемь наблюдений будем использовать для построения линейного тренда и выделения сезонной составляющей; следующие двенадцать наблюдений – для настройки параметров адаптации; оставшиеся четыре будут использованы в качестве контрольной выборки.

Рис. 51. Динамика прибыли компании
Используя МНК, по первым восьми наблюдениям построим трендовую модель  (см. Вывод итогов 19), параметры которой принимаются за начальные значения
(см. Вывод итогов 19), параметры которой принимаются за начальные значения  и
и  .
.
| ВЫВОД ИТОГОВ 19 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,799098 | |||||
| R-квадрат | 0,638557 | |||||
| Нормированный R-квадрат | 0,578317 | |||||
| Стандартная ошибка | 10,3318 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1131,524 | 1131,524 | 10,60015 | 0,01734 | ||
| Остаток | 640,4762 | 106,746 | ||||
| Итого | ||||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 32,14286 | 8,050471 | 3,992668 | 0,007179 | 12,44405 | 51,84167 |
| Переменная X 1 | 5,190476 | 1,594231 | 3,255787 | 0,01734 | 1,289531 | 9,091422 |
Вычислим расчетные значения
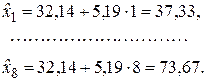
Выделим сезонную составляющую путем деления фактических значений на расчетные значения по трендовой модели

и получим усредненные оценки сезонных составляющих

В качестве начальных значений параметров адаптации выберем  ,
,  ,
,  .
.
Осуществим адаптивную настройку параметров модели. Для этого при заданных начальных значениях 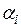 ,
,  проведем расчет на данных обучающей выборки (с 9-го по 16-е наблюдение) текущих значений коэффициентов тренда и сезонной составляющей
проведем расчет на данных обучающей выборки (с 9-го по 16-е наблюдение) текущих значений коэффициентов тренда и сезонной составляющей

Проведем постпрогнозные расчеты для 17 – 20 наблюдений и вычислим относительные ошибки

Подберем параметры адаптации таким образом, чтобы максимальная относительная ошибка была минимальной. Минимальное значение максимальной относительной ошибки  получено при
получено при 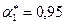 ,
, 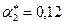 ,
,  . Все расчеты сведены в табл. 77.
. Все расчеты сведены в табл. 77.
Т а б л и ц а 77
Результаты моделирования прибыли компании

| 
| 
| 
| 
| 
| 
| |
| Данные для построения линейного тренда | 37,33 | 0,80 | |||||
| 42,52 | 1,01 | ||||||
| 47,71 | 1,26 | ||||||
| 52,90 | 0,98 | ||||||
| 58,10 | 0,83 | 0,81 | |||||
| 63,29 | 1,06 | 1,03 | |||||
| 68,48 | 1,20 | 1,23 | |||||
| 73,67 | 0,84 | 0,91 | |||||
| Данные для настройки параметров адаптации | 0,88 | 69,48 | 9,05 | ||||
| 1,04 | 77,36 | 8,91 | |||||
| 1,23 | 78,61 | 7,99 | |||||
| 0,91 | 77,23 | 6,86 | |||||
| 0,88 | 72,97 | 5,53 | |||||
| 1,06 | 85,89 | 6,42 | |||||

| 1,23 | 88,14 | 5,92 | ||||
| 0,90 | 79,81 | 4,21 | |||||
| 73,96 | -4,16 | 0,88 | 80,82 | 3,82 | |||
| 93,20 | 1,90 | 1,06 | 89,66 | 4,43 | |||
| 113,73 | 2,80 | 1,24 | 95,04 | 4,54 | |||
| 87,37 | -2,79 | 0,90 | 94,29 | 3,90 | |||
| Контрольная выборка | 86,50 | -4,22 | |||||
| 108,71 | -2,55 | ||||||
| 130,98 | -3,95 | ||||||
| 99,30 | -2,37 |
Таким образом, модель для прогнозирования динамики прибыли в окончательном виде может быть записана следующим образом:
 ,
,
где  .
.
Осуществим расчет прогнозных оценок и сравним их с данными контрольной выборки
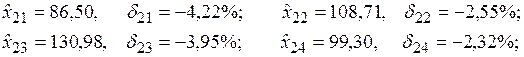
Результаты расчетов свидетельствует о том, что с помощью построенной модели удается осуществить достаточно точную экстраполяцию динамики прибыли компании «Восход».
Задание 16. Фирма «Наслаждение» вот уже пять лет довольно успешно занимается выпечкой тортов и пирожных, данные о среднесуточных продажах которых представлены в табл. 88. Эта таблица была сформирована с учетом специфики производимой продукции (на кондитерские изделия спрос естественным образом повышается в предпраздничные и праздничные дни), поэтому год был разбит на 8 условных периодов, характеризующихся своим среднесуточным объемом продаж. Очевидно, что периоды повышения спроса связаны не только с увеличением выручки, но и с ростом прямых и косвенных затрат, связанных с наймом дополнительной рабочей силы, увеличением продолжительности рабочего дня, закупкой в большем объеме необходимых для выпечки кондитерских изделий продуктов и т.д. В связи с этим руководство фирмы заинтересовано в том, чтобы заранее подготовиться к таким периодам, получив прогнозные оценки среднесуточных объемов продаж тортов и пирожных в предпраздничные и праздничные периоды. Рассчитайте требуемые прогнозные оценки.
Т а б л и ц а 78
| Год | Среднесуточный объем продаж тортов и пирожных фирмой "Наслаждение", кг. | |||||||
| 9.01-19.02 | 19.02-24.02 | 25.02-3.03 | 4.03-9.03 | 10.03-29.04 | 30.04-3.05 | 4.05-20.12 | 21.12-8.01 | |
Задание 17. В табл. 79 представлены квартальные данные об объемах продаж продукции предприятий сахарной подотрасли Воронежской области за 2002 г. Получите прогнозные оценки объема продаж на 2005 г.
Т а б л и ц а 79
| Год | Квартал | Объем продаж, тыс. руб. | Год | Квартал | Объем продаж, тыс. руб. |
| I | 257,10 | I | 257,64 | ||
| II | 171,40 | II | 171,76 | ||
| III | 85,70 | III | 85,88 | ||
| IV | 1199,80 | IV | 1202,32 | ||
| I | 245,94 | I | 354,63 | ||
| II | 163,96 | II | 236,42 | ||
| III | 81,98 | III | 118,21 | ||
| IV | 1147,72 | IV | 1654,94 |
Задание 18. Динамика объема сбыта мороженого «Пломбир» ЗАО «Белоснежка» представлена в табл. 80. Рассчитайте прогнозные оценки на следующие три месяца.
Т а б л и ц а 80
| № п.п. | Месяц | Объем продаж, руб. | № п.п. | Месяц | Объем продаж, руб. |
| 1. | июль | 8174,40 | 13. | июль | 8991,84 |
| 2. | август | 5078,33 | 14. | август | 5586,16 |
| 3. | сентябрь | 4507,21 | 15. | сентябрь | 4957,92 |
| 4. | октябрь | 2257,20 | 16. | октябрь | 2482,92 |
| 5. | ноябрь | 3400,70 | 17. | ноябрь | 3740,77 |
| 6. | декабрь | 2968,72 | 18. | декабрь | 3265,59 |
| 7. | январь | 2147,14 | 19. | январь | 2361,86 |
| 8. | февраль | 1325,57 | 20. | февраль | 1458,12 |
Окончание табл. 80
| 9. | март | 2290,96 | 21. | март | 2520,05 |
| 10. | апрель | 2953,34 | 22. | апрель | 3248,67 |
| 11. | май | 4216,28 | 23. | май | 4637,91 |
| 12. | июнь | 8227,57 | 24. | июнь | 9050,33 |
Задание 19. Табл. 81 представляет временной ряд по показателю потребления безалкогольного напитка «Тархун» в декалитрах в одном из регионов РФ начиная с 1993 г. Рассчитайте ежемесячные прогнозные оценки потребления этого напитка на 2000 г.
Date: 2016-02-19; view: 577; Нарушение авторских прав