С автокоррелированными остатками

Пример 7. Госпожа Арешникова В.В., руководитель компании «Преслава», собрала данные о месячных объемах продаж своей компании (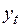, тыс. руб.) вместе с несколькими другими показателями, как она полагала, способными оказывать влияние на объем продаж. В качестве этих показателей ею были выбраны расходы на рекламу (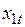, тыс. руб.) и индекс потребительских расходов (, %). Собранные госпожой Арешниковой В.В. данные представлены в табл. 33. Требуется оценить степень взаимосвязи между этими показателями, построив соответствующее линейное уравнение регрессии. Для построенного уравнения следует проверить гипотезу о наличии автокорреляции в остатках. В случае подтверждения этой гипотезы необходимо оценить параметры регрессии обобщенным МНК и получить прогнозную оценку объема продаж на следующий месяц при условии того, что расходы на рекламу составят 7,9 тыс. руб., а индекс потребительских расходов возрастет до 114,9 %.

Т а б л и ц а 33

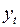
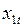
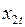
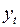
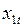
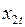
		4,0	97,9			14,6	109,2
		5,8	98,4			10,2	110,1
		4,6	101,2			8,5	110,7
		6,7	103,5			6,2	110,3
		8,7	104,1			8,4	111,8
		8,2	107,0			8,1	112,3
		9,7	107,4			6,9	112,9
		12,7	108,5			7,5	113,1
		13,5	108,3			7,7	113,4

Решение с помощью Excel

1. Ввод исходных данных с включением в модель дополнительной переменной , принимающей единственное значение, равное 1.

2. Нахождение вектора оценок коэффициентов регрессии с использованием матричных функций Excel (МУМНОЖ, ТРАНСП, МОБР)

.

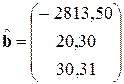3. Расчет остатков .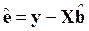

4. Вычисление разностей 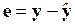и оформление промежуточных результатов в виде табл. 34.

Т а б л и ц а 34

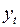
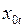
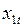
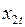
				97,9	234,74	17,26
			5,8	98,4	286,43	-12,43
			4,6	101,2	346,93	-50,93
			6,7	103,5	459,27	-77,27
			8,7	104,1	518,06	29,94
			8,2		595,80	144,20
			9,7	107,4	638,37	125,63
			12,7	108,5	732,62	57,38
			13,5	108,3	742,80	-8,80
			14,6	109,2	792,40	-58,40
			10,2	110,1	730,35	-88,35
			8,5	110,7	714,02	-100,02
			6,2	110,3	655,21	6,79
			8,4	111,8	745,33	-55,33
			8,1	112,3	754,39	-26,39
			6,9	112,9	748,21	19,79
			7,5	113,1	766,46	24,54
			7,7	113,4	779,61	52,39

5. Проверка гипотезы о наличии автокорреляции в остатках

5.1. Проверка гипотезы о наличии автокорреляции в остатках с использованием критерия Дарбина – Уотсона.

5.1.1. Вычисление 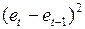и . Оформление результатов расчетов в виде табл. 35.

Т а б л и ц а 35

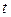
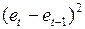
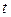
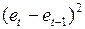
	298,00			3411,10	2460,98
	154,61	881,91		7806,06	896,84
	2593,94	1481,98		10004,50	136,20
	5970,72	693,78		46,17	11409,94
	896,49	11494,40		3061,38	3859,45
	20794,50	13055,69		696,56	837,36
	15782,21	345,06		391,48	2132,44
	3292,91	4657,16		602,38	22,63
	77,38	4379,83		2744,81	775,49
	Сумма	78625,21	59521,14

5.1.2. Расчет статистики Дарбина – Уотсона

=59521,14 / 78625,21= 0,757.

Так как 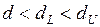, т.е. 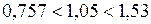, то существует положительная автокорреляция остатков.

5.2. Проверка гипотезы о наличии автокорреляции в остатках с использованием метода рядов.

Последовательное определение знаков отклонений позволяет получить следующие ряды:

(+) (– – –) (+ + + +) (– – – –) (+) (– –) (+ + +)

и сделать вывод о присутствии автокорреляции в остатках.

5.3. Проверка гипотезы о наличии автокорреляции в остатках с использованием графического представления зависимости остатков от времени (рис. 13).

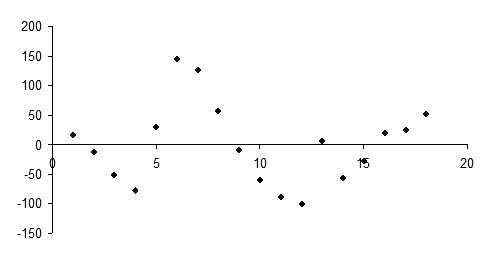
Р и с. 13. График зависимости остатков от времени

Анализ построенного графика показывает, что изменение остатков подчиняется некоторой закономерности и можно сделать вывод о том, что они автокоррелированы.

Наличие автокорреляции означает, что 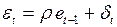, т.е. не выполняются предположения классического регрессионного анализа, и, следовательно, можно найти более эффективную оценку, чем .

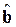6. Преобразование исходных данных.

6.1. Оценка параметра .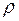

6.1.1. Вычисление 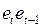и оформление результатов расчетов в виде табл. 36.

Т а б л и ц а 36

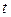
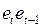
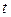
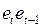
	17,26	298,00			-58,40	3411,10	513,75
	-12,43	154,61	-214,65		-88,35	7806,06	5160,16
	-50,93	2593,94	633,29		-100,02	10004,50	8837,18
	-77,27	5970,72	3935,44		6,79	46,17	-679,63
	29,94	896,49	-2313,59		-55,33	3061,38	-375,95
	144,20	20794,50	4317,65		-26,39	696,56	1460,29
	125,63	15782,21	18115,83		19,79	391,48	-522,20
	57,38	3292,91	7208,98		24,54	602,38	485,61
	-8,80	77,38	-504,77		52,39	2744,81	1285,85
	Сумма	78625,21	47343,24

6.1.2. Вычисление коэффициента автокорреляции

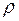= 47343,24 / 78625,21 = 0,6021.

6.2. Преобразование исходных данных и оформление результатов расчетов в виде табл. 37.

Т а б л и ц а 37

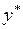
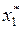
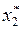
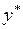
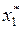
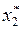
	201,19	0,80	3,19	78,16		292,03	0,40	6,47	43,99
	122,26	0,40	3,39	39,45		200,03	0,40	1,41	44,35
	131,01	0,40	1,11	41,95		227,43	0,40	2,36	44,40
	203,77	0,40	3,93	42,56		292,29	0,40	1,08	43,64
	317,98	0,40	4,67	41,78		291,38	0,40	4,67	45,38
	410,03	0,40	2,96	44,32		312,52	0,40	3,04	44,98
	318,42	0,40	4,76	42,97		329,64	0,40	2,02	45,28
	329,97	0,40	6,86	43,83		328,56	0,40	3,35	45,12
	258,31	0,40	5,85	42,97		355,71	0,40	3,18	45,30

7. Оценка с помощью обычного МНК вектора коэффициентов регрессии 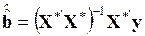с использованием матричных функций Excel (ТРАНСП, МОБР, МУМНОЖ)

.

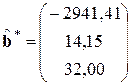8. Нахождение прогнозной оценки объема продаж на следующий период

при 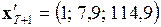и с учетом того, что коррелированно с предыдущим значением в выборочном периоде

815,79+0,60 (832 – 796,96) = 836,89.

Задание 7. Аналитику Воронежского филиала энергетической компании было поручено разработать новые тарифы на электроэнергию, для чего ему потребовалось составить прогноз расходов населения на электроэнергию на следующий период. С этой целью он решил исследовать две потенциально независимые переменные: цена на электроэнергию для физических лиц (коп. за кВт/ч, 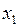) и потребление электроэнергии населением (кВт/ч, 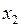). Ему удалось собрать данные по этим показателям за 20 периодов (см. табл. 38).

Т а б л и ц а 38

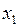
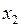
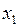
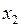
	28,95	1,33			113,60	2,74
	41,70	1,58			127,80	2,65
	51,30	1,92			136,95	3,15
	70,05	1,96			142,20	3,25
	66,75	1,98			152,25	3,25
	81,45	2,05			154,05	3,85
	77,40	2,16			153,23	3,97
	97,80	2,34			181,60	3,97
	107,70	2,56			186,30	4,13
	111,90	2,62			195,40	4,35

Когда аналитик делал доклад на комиссии по тарифам, ему бы задан вопрос: «Так как данные представляют временной ряд, то не будут ли Ваши расчеты искажены автокоррелированностью остатков?». Ответьте на этот вопрос и рассчитайте прогнозную оценку расходов населения на электроэнергию на следующий период при условии того, что цена на электроэнергию составит 4,34 коп. за кВТ/ч, а потребление электроэнергии – 14905кВт.