
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Множественная регрессия
|
|
Пример 2. Руководство ОАО «Железные дороги» вынуждено периодически повышать цены на свои услуги. То, что повышение цен явно негативным образом влияет на число пассажиров, пользующихся услугами железной дороги, можно понять, проанализировав, в частности, данные табл. 8.
Т а б л и ц а 8
Показатели, характеризующие деятельность ОАО «Железные дороги»
| Стоимость проезда 1 чел. в поезде Воронеж – Москва, руб. | Среднемесячное число пассажиров поезда Воронеж – Москва | Стоимость проезда 1 чел. в поезде Воронеж – Москва, руб. | Среднемесячное число пассажиров поезда Воронеж – Москва |
Руководство планирует в следующем периоде поднять цены на билеты для пассажиров поезда Воронеж – Москва. В этой связи было решено поручить студенту экономического факультета, проходящему практику в отделе экономического анализа управления железной дороги, известным ему методом спрогнозировать среднемесячное число пассажиров поезда при условии, что билет на этот поезд будет стоить 690 руб. Студент-практикант решил применить к имеющимся данным регрессионный анализ и, воспользовавшись его результатами, получить требуемую прогнозную оценку.
Решение с помощью MS Excel
1. Ввод исходных данных.
2. Подготовка данных для расчета оценок коэффициентов линейной регрессии и оформление их в виде табл. 9.
Т а б л и ц а 9
Промежуточные расчеты оценок коэффициентов регрессионного уравнения
| № п.п. | 
| 
| 
| 
| 
|
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| 8. | |||||
| 9. | |||||
| 10. | |||||
| 11. | |||||
| 12. | |||||
| 13. | |||||
| 14. | |||||
| 15. | |||||
| 16. | |||||
| Средние значения | 416,88 | 10918,13 | 205268,75 | 4349625,00 | 120652931,25 |
3. Расчет оценок коэффициентов регрессии
 ,
,  .
.
Таким образом, построенная модель может быть записана в виде
 .
.
Коэффициент  этой модели показывает, что в среднем увеличение стоимости проезда на 1 руб. приводит к уменьшению числа пассажиров на 6 человек.
этой модели показывает, что в среднем увеличение стоимости проезда на 1 руб. приводит к уменьшению числа пассажиров на 6 человек.
4. Расчет коэффициентов корреляции и детерминации
 ;
;  ;
;
 ;
; 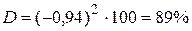 .
.
Коэффициент корреляции достаточно высокий, что свидетельствует о существенной зависимости среднемесячного числа пассажиров от стоимости проезда. Коэффициент детерминации также достаточно высокий, он показывает, что число пассажиров объясняется стоимостью проезда на 89%.
5. Расчет дисперсионного отношения Фишера
 .
.
Сравнение расчетного значения F -критерия с табличным  для 5%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
для 5%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
6. Расчет стандартных ошибок по формулам, в которых используется средняя квадратическая ошибка  , вычисленная в соответствии с данными табл. 10.
, вычисленная в соответствии с данными табл. 10.
 ,
,  .
.
Т а б л и ц а 10
Промежуточные расчеты стандартных ошибок
| № п.п. | 
| 
| 
| 
|
| 1. | 12436,92 | 2201,04 | ||
| 2. | 12436,92 | 26596,64 | ||
| 3. | 12116,33 | 42570,52 | ||
| 4. | 12116,33 | 31090,95 | ||
| 5. | 12116,33 | 287645,85 | ||
| 6. | 11378,97 | 123220,91 | ||
| 7. | 11378,97 | 12327,30 | ||
| 8. | 11378,97 | 442,19 | ||
| 9. | 10641,62 | 669750,71 | ||
| 10. | 10641,62 | 135706,02 | ||
| 11. | 10641,62 | 467,30 | ||
| 12. | 9904,26 | 45908,38 | ||
| 13. | 9904,26 | 155442,84 | ||
| 14. | 9198,97 | 450285,72 | ||
| 15. | 9198,97 | 83501,74 | ||
| 16. | 9198,97 | 383119,74 | ||
| Сумма квадратов отклонений расчетных от фактических значений | 2450277,85 | |||
| Среднеквадратическая ошибка | 418,35 |
7. Расчет t -статистик Стьюдента
 ,
, 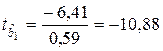 .
.
Сравнение расчетных значений с табличным 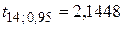 (см. Приложение) подтверждает значимость коэффициентов регрессии.
(см. Приложение) подтверждает значимость коэффициентов регрессии.
8. Расчет доверительных границ для коэффициентов регрессии
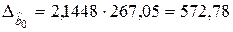 ,
,  ,
,
 ;
;  ;
;
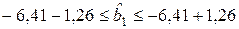 ;
;  .
.
9. Построение линейного уравнения регрессии и расчет всех его характеристик с помощью пакета «Анализ данных» Excel (см. Вывод итогов 3)
| ВЫВОД ИТОГОВ 3 | |||||||
| Регрессионная статистика | |||||||
| Множественный R | 0,945622 | ||||||
| R-квадрат | 0,894201 | ||||||
| Нормированный R-квадрат | 0,886643 | ||||||
| Стандартная ошибка | 418,3537 | ||||||
| Наблюдения | |||||||
| Дисперсионный анализ | |||||||
| df | SS | MS | F | Значимость F | |||
| Регрессия | 118,3258 | 3,26E-08 | |||||
| Остаток | 175019,8 | ||||||
| Итого | |||||||
| Коэффи-циенты | Стандарт-ная ошибка | t-статис-тика | P-Зна-чение | Нижние 95% | Верхние 95% | ||
| Y-пересечение | 13591,04 | 267,0547 | 50,89233 | 2,73E-17 | 13018,26 | 14163,81 | |
| Переменная X 1 | -6,41178 | 0,589439 | -10,8778 | 3,26E-08 | -7,676 | -5,14756 | |
10. Получение прогнозной оценки числа пассажиров
 .
.
11. Расчет доверительных границ прогнозной оценки
 ,
,
 .
.
Пример 3. Экономисту-аналитику одной крупной компании было поручено указать обоснованный размер заработной платы руководителя будущего филиала этой компании. Ожидаемый объем среднемесячных продаж филиала составит 6500 тыс. у.е. Сотрудник, который, как планируется, должен занять пост руководителя, имеет законченное высшее образование, а срок работы в должности директора другого филиала компании – 3 года. С целью решения поставленной задачи экономист-аналитик решил сначала изучить опыт других компаний, собрав сведения, представленные в табл. 11, в которой за  обозначена среднемесячная заработная плата руководителей, у.е.; за
обозначена среднемесячная заработная плата руководителей, у.е.; за 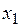 – образование (0 – нет высшего образование, 1 – незаконченное высшее, 2 – высшее); за
– образование (0 – нет высшего образование, 1 – незаконченное высшее, 2 – высшее); за  – срок работы в должности руководителя, лет; за
– срок работы в должности руководителя, лет; за  – годовой объем продаж компании, тыс. у.е.
– годовой объем продаж компании, тыс. у.е.
Т а б л и ц а 11
Данные о 30 российских компаниях
| Компания | 
| 
| 
| 
| Компания | 
| 
| 
| 
|
| 1 652 | 12 949 | ||||||||
| 1 948 | 1 227 | 5 061 | |||||||
| 1 735 | 1 712 | 1 929 | |||||||
| 1 681 | 1 488 | 2 643 | |||||||
| 1 461 | 5 673 | 1 084 | |||||||
| 1 117 | 1 752 | 5 137 | |||||||
| 1 475 | 2 497 | ||||||||
| 2 094 | 10 818 | 2 097 | |||||||
| 2 686 | 2 342 | ||||||||
| 3 409 | 14 021 | ||||||||
| 2 244 | 4 451 | ||||||||
| 1 539 | 1 911 | ||||||||
| 2 833 | 11 663 | 1 554 | 1 435 | ||||||
| 2 366 | 1 314 | ||||||||
| 1 856 | 4 864 | 2 301 |
Постройте модель множественной регрессии, отражающую зависимость среднемесячной зарплаты от указанных факторов, и оцените ее качество. Используя построенную модель, осуществите прогнозный расчет заработной платы руководителя будущего филиала компании.
Решение с помощью табличного процессора Excel
1. Ввод исходных данных с включением дополнительной переменной  , принимающей единственное значение, равное 1.
, принимающей единственное значение, равное 1.
2. Расчет коэффициентов регрессии с использованием матричных функций Excel: ТРАНСП, МУМНОЖ, МОБР.
 ;
;
 ;
;  .
.
Таким образом, построенная модель имеет следующий вид:
 .
.
3. Расчет стандартных ошибок коэффициентов регрессии
3.1. Проведение промежуточных расчетов, требуемых для расчета остаточной дисперсии, и оформление их в виде табл. 12.
Т а б л и ц а 12
Промежуточные расчеты остаточной дисперсии
| Компания | 
| 
| 
| Компания | 
| 
| 
|
| 1154,46 | 492052,43 | 1228,95 | 199768,26 | ||||
| 1797,72 | 22583,26 | 600,01 | 168,62 | ||||
| 1517,37 | 47362,93 | 1320,89 | 27926,87 | ||||
| 1475,62 | 693262,60 | 884,43 | 191345,71 | ||||
| 1612,90 | 23074,14 | 1440,71 | 96899,55 | ||||
| 155,91 | 40439,03 | 1315,31 | 1396383,37 | ||||
| 597,15 | 5162,82 | 902,41 | 18066,92 | ||||
| 2108,75 | 217,54 | 2209,70 | 17503,54 | ||||
| 1206,63 | 371645,73 | 2951,09 | 209677,47 | ||||
| 598,86 | 84182,61 | 1372,47 | 759562,00 | ||||
| 193,73 | 102571,43 | 1127,68 | 277391,76 | ||||
| 603,32 | 18855,47 | 1206,59 | 120690,40 | ||||
| 2435,51 | 158000,95 | 583,76 | 14825,39 | ||||
| 1214,55 | 620228,48 | 433,56 | 23543,75 | ||||
| 1330,50 | 276149,72 | Сумма квадратов отклонений | 7132998,11 | ||||
| 2559,44 | 823455,38 | Остаточная дисперсия | 274346,08 |
3.2. Получение стандартных ошибок
 ;
;  ;
;
 ;
;  .
.
4. Расчет t -статистик
 ;
;  ;
;
 ;
;  .
.
Сравнение полученных t -статистик с табличным значением  (см. Приложение) подтверждает значимость таких коэффициентов регрессии, как
(см. Приложение) подтверждает значимость таких коэффициентов регрессии, как  ,
,  ,
,  , и незначимость коэффициента
, и незначимость коэффициента  .
.
5. Вычисление множественного коэффициента корреляции.
5.1. Проведение промежуточных расчетов и оформление их в виде табл. 13.
Т а б л и ц а 13
Промежуточные расчеты множественного коэффициента корреляции
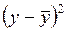
| 
| 
| 
|
| 669669,44 | 1,36 | 193,21 | 7187046,08 |
| 457877,78 | 0,69 | 118,81 | 5409655,75 |
| 214986,78 | 0,69 | 8,41 | 3388790,08 |
| 394802,78 | 0,03 | 118,81 | 3503884,82 |
| 35973,44 | 0,69 | 16,81 | 4494965,35 |
| 836005,44 | 1,36 | 123,21 | 5933446,42 |
| 362805,44 | 0,03 | 102,01 | 4317529,88 |
| 676780,44 | 0,69 | 16,81 | 52782162,35 |
| 454725,44 | 1,36 | 118,81 | 751457,82 |
| 146178,78 | 0,03 | 50,41 | 11108000,22 |
| 573553,78 | 1,36 | 82,81 | 8362892,82 |
| 648561,78 | 0,03 | 102,01 | 4055658,95 |
| 2438802,78 | 0,69 | 3,61 | 65774262,68 |
| 712898,78 | 0,03 | 8,41 | 1408652,48 |
| 341835,11 | 0,69 | 82,81 | 1719070,62 |
| 144907,11 | 0,69 | 3,61 | 88287321,62 |
| 239447,11 | 0,03 | 9,61 | 2274466,15 |
| 433402,78 | 0,03 | 123,21 | 2636942,95 |
| 46944,44 | 0,69 | 16,81 | 827857,35 |
| 679525,44 | 0,69 | 123,21 | 6095302,62 |
| 231040,44 | 0,03 | 3,61 | 2509478,42 |
| 1502258,78 | 1,36 | 320,41 | 7337958,62 |
| 253344,44 | 0,03 | 16,81 | 2119547,75 |
| 1146327,11 | 0,69 | 479,61 | 7386799,22 |
| 4569618,78 | 0,03 | 320,41 | 109581815,48 |
| 946080,44 | 0,69 | 50,41 | 806643,48 |
| 449346,78 | 0,69 | 50,41 | 2695726,15 |
| 79900,44 | 0,03 | 24,01 | 4485359,22 |
| 655020,44 | 1,36 | 1,21 | 5012523,95 |
| 468312,11 | 1,36 | 50,41 | 1567170,15 |
| Сумма квадратов отклонений | |||
| 20810934,67 | 18,17 | 2740,70 | 423822389,47 |
| Дисперсия | |||
| 717618,44 | 0,63 | 94,51 | 14614565,15 |
| Среднеквадратическое отклонение | |||
| 847,12 | 0,79 | 9,72 | 3822,90 |
5.2. Расчет множественного коэффициента корреляции
 .
.
Множественный коэффициент корреляции достаточно высокий, что свидетельствует о существенной зависимости величины заработной платы от включенных в модель факторов.
6. Расчет бета-коэффициентов
 ;
;
 ;
;
 .
.
Полученные значения бета-коэффициенты позволяют проранжировать факторы по степени их влияния на моделируемый показатель следующим образом:
1) стаж работы в должности руководителя (в большей степени влияющий фактор);
2) годовой объем продаж компании;
3) образование (в меньшей степени влияющий фактор).
7. Вычисление парных коэффициентов корреляции.
7.1. Проведение промежуточных расчетов и оформление результатов расчетов в виде табл. 14.
Т а б л и ц а 14
Промежуточные расчеты парных коэффициентов корреляции
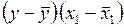
| 
| 
|
| 954,72 | -11374,83 | 2193842,56 |
| 563,89 | 7375,67 | -1573836,44 |
| 386,39 | 1344,63 | -853548,51 |
| 104,72 | -6848,83 | 1176156,22 |
| 158,06 | -777,63 | 402118,62 |
| 1066,72 | 10149,10 | 2227194,09 |
| 100,39 | 6083,57 | 1251568,36 |
| 685,56 | -3372,93 | 5976783,02 |
| 786,72 | -7350,23 | 584557,09 |
| 63,72 | 2714,57 | 1274266,02 |
| 883,56 | 6891,73 | 2190107,02 |
| 134,22 | 8133,87 | 1621833,96 |
| 1301,39 | 2967,17 | 12665324,89 |
| 140,72 | -2448,57 | 1002111,09 |
| 487,22 | -5320,47 | 766575,96 |
| 317,22 | 723,27 | 3576794,76 |
| 81,56 | 1516,93 | -737979,91 |
| 109,72 | 7307,50 | 1069045,56 |
| 180,56 | -888,33 | -197137,78 |
| -686,94 | 9150,10 | 2035169,09 |
| -80,11 | 913,27 | 761440,09 |
| -1429,94 | 21939,43 | -3320167,58 |
| 83,89 | 2063,67 | 732786,22 |
| 892,22 | 23447,60 | -2909929,24 |
| -356,28 | 38264,23 | 22377379,69 |
| 810,56 | -6905,93 | 873584,36 |
| -558,61 | 4759,37 | 1100597,96 |
Окончание табл. 14
| -47,11 | 1385,07 | -598650,31 |
| 944,22 | 890,27 | 1811989,42 |
| 798,39 | 4858,77 | 856694,09 |
| Суммы произведений | ||
| 8877,33 | 117592,00 | 58336670,33 |
7.2. Расчет парных коэффициентов корреляции
 ;
;  ;
;
 .
.
8. Вычисление дисперсионного отношения Фишера
 .
.
Сравнение расчетного значения F -критерия с табличным  для 5%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
для 5%-го уровня значимости (см. Приложение) позволяет сделать вывод об адекватности построенной модели.
9. Построение с помощью «Пакета анализа» линейного регрессионного уравнения (см. Вывод итогов 4).
| ВЫВОД ИТОГОВ 4 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,8107080 | |||||
| R-квадрат | 0,6572475 | |||||
| Нормированный R-квадрат | 0,617699 | |||||
| Стандартная ошибка | 523,78056 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 4559312,19 | 16,618834 | 3,11E-06 | |||
| Остаток | 7132998,1 | 274346,081 | ||||
| Итого | ||||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Зна- чение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 7,3681327 | 219,864 | 0,033512 | 0,9735221 | -444,57 | 459,306 |
| Переменная X 1 | 365,8528 | 133,786 | 2,734594 | 0,0110946 | 90,8498 | 640,855 |
| Переменная X 2 | 40,886834 | 10,2142 | 4,002904 | 0,0004639 | 19,8910 | 61,8826 |
| Переменная X 3 | 0,0963746 | 0,02780 | 3,466448 | 0,0018469 | 0,03922 | 0,15352 |
10. Использование построенной модели в прогнозных целях
 у.е.
у.е.
Решение с помощью системы STATISTICA
1. Ввод исходных данных (без включения дополнительной переменной).
2. Вызов модуля «Множественная регрессия» (Статистика / Множественная регрессия, см. рис. 2).

Рис. 2. Меню Статистика
3. Выбор переменных для анализа (Multiple Linear regressions / Variables / OK / Select dependent and independent variable lists / OK, см. рис. 3).

Рис. 3. Выбор переменных для анализа (dependent var. – зависимая переменная;
independent variable list – независимые переменные)
После нажатия кнопки «ОК» появится окно, представленное на рис. 4. В нем использованы следующие обозначения: Multiple R – множественный R (множественный коэффициент корреляции); R? – R-квадрат (множественный коэффициент детерминации); adjusted R? – скорректированный R-квадрат; F – F-критерий (дисперсионное отношение Фишера); p – значимость F; df – число степеней свободы числителя (в данном случае – 3) и знаменателя (в данном случае – 26); Standard error of estimate – стандартная ошибка; Intercept – свободный члена ( ); Std. Error – стандартная ошибка коэффициента
); Std. Error – стандартная ошибка коэффициента  ; далее показана t-статистика и p-значение, позволяющие определить степень статистической значимости
; далее показана t-статистика и p-значение, позволяющие определить степень статистической значимости  . Под чертой приводятся значения бета-коэффициентов. Красный шрифт свидетельствует об их значимости.
. Под чертой приводятся значения бета-коэффициентов. Красный шрифт свидетельствует об их значимости.

Рис. 4. Вкладка Multiple Regression Results
(Результаты множественного регрессионного анализа)
4. Переход на вкладку Summary: Regression results (Результаты быстрого регрессионного анализа, см. рис. 8). На ней представлены: бета-коэффициенты (Beta), стандартные ошибки бета-коэффициентов (Std. Err. of Beta), оценки коэффициентов регрессионного уравнения b (B), стандартные ошибки оценок коэффициентов b (Std. Err. of B), t -статистики Стьюдента (t (15)), p -значения (p-level). Красный шрифтом свидетельствует о значимости коэффициентов регрессии.

Рис. 5. Вкладка Regression Summary for Dependent Variable: Y
(Результаты регрессионного анализа для переменной Y)
5. Переход на вкладку Advanced / Descriptive statistics / Correlations (Расширенный анализ / Описательные статистики / Корреляция, см. рис. 6– 8). В результате появится матрица корреляций между переменными модели.

Рис. 6. Вкладка Advanced (Расширенный анализ)

Рис. 7. Вкладка Review Descriptive Statistics
(Просмотр описательных статистик)
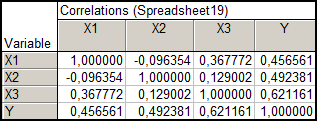
Рис. 8. Матрица корреляций
6. Переход на вкладку Summary: Predicted & Residual Values (Предсказанные значения и остатки, см. рис. 9). Здесь использованы следующие обозначения: Observed Value – наблюдаемые (фактические) значения, Predicted Value – предсказанные (расчетные) значения, Residual – остатки; Minimum – минимальное значение, Maximum – максимальное значение, Mean – среднее, Median – медиана. Графическое отображение фактических и расчетных значений можно получить, выполнив следующий пункт.

Рис. 9. Вкладка Predicted & Residual Values (Предсказанные значения и остатки)
7. Переход на вкладку Scatterplots (Графики, см. рис. 10), выбор Predected vs. Observed (Предсказанные и фактические значения, см. рис. 11).
Пример 4. Известно, что стоимость выпуска газеты в значительной степени определяется величиной типографских расходов. Для того чтобы иметь возможность воздействовать на эту стоимость, издатели наиболее популярных газет решили изучить факторы, определяющие сумму годовых затрат на печать газет, и оценить степень их влияния. С этой целью для 20 городов России были собраны данные о годовых расходах на печать ( , млн. руб.), объемах розничной продажи газет в городе (млн. руб.) и количества семей в городе (в тысячах). Заметим, что для факторов были взяты их логарифмы (
, млн. руб.), объемах розничной продажи газет в городе (млн. руб.) и количества семей в городе (в тысячах). Заметим, что для факторов были взяты их логарифмы (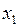 и
и 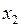 , соответственно) с целью уменьшения разброса данных, а, следовательно, и упрощения их обработки. Все эти данные представлены в табл. 15. Постройте модель множественной регрессии, отражающую зависимость среднегодовых расходов на издание газеты от соответствующих факторов.
, соответственно) с целью уменьшения разброса данных, а, следовательно, и упрощения их обработки. Все эти данные представлены в табл. 15. Постройте модель множественной регрессии, отражающую зависимость среднегодовых расходов на издание газеты от соответствующих факторов.

Рис. 10. Вкладка Scatterplots (Графики)

Рис. 11. Предсказанные и фактические значения зависимой переменной Y
Т а б л и ц а 15
| № п.п. | 
| 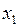
| 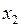
| № п.п. | 
| 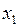
| 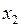
|
| 1. | 2,8 | 4,4 | 3,00 | 11. | 2,7 | 4,24 | 2,89 |
| 2. | 2,3 | 3,68 | 2,51 | 12. | 2,9 | 4,72 | 3,22 |
| 3. | 2,5 | 3,92 | 2,67 | 13. | 3,3 | 5,28 | 3,6 |
| 4. | 2,7 | 4,32 | 2,94 | 14. | 2,7 | 4,24 | 2,89 |
| 5. | 2,6 | 4,24 | 2,89 | 15. | 1,8 | 3,04 | 2,07 |
| 6. | 2,4 | 3,76 | 2,56 | 16. | 1,9 | 3,12 | 2,13 |
| 7. | 3,5 | 5,52 | 3,76 | 17. | 2,2 | 3,6 | 2,46 |
| 8. | 2,1 | 3,36 | 2,29 | 18. | 2,3 | 3,68 | 2,51 |
| 9. | 1,9 | 3,04 | 2,07 | 19. | 3,6 | 5,76 | 3,92 |
| 10. | 3,8 | 5,92 | 4,03 | 20. | 2,2 | 3,6 | 2,45 |
Решение с помощью табличного процессора Excel
1. Ввод исходных данных.
2. Построение регрессионного уравнения с использованием «Пакета анализа» (см. Вывод итогов 5) и анализ полученных результатов.
| ВЫВОД ИТОГОВ 5 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,997299 | |||||
| R-квадрат | 0,994606 | |||||
| Нормированный R-квадрат | 0,993972 | |||||
| Стандартная ошибка | 0,044773 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 6,283922 | 3,141961 | 1567,374 | 5,26E-20 | ||
| Остаток | 0,034078 | 0,002005 | ||||
| Итого | 6,318 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -0,10201 | 0,052759 | -1,93359 | 0,069992 | -0,21333 | 0,009298 |
| Переменная X 1 | 2,653207 | 2,446084 | 1,084675 | 0,293209 | -2,50759 | 7,814002 |
| Переменная X 2 | -2,93956 | 3,595708 | -0,81752 | 0,424942 | -10,5258 | 4,646732 |
Анализ Вывода итогов 5 свидетельствует о том, что полученные стандартные ошибки значительно больше самих расчетных коэффициентов. Коэффициенты при факторах 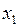 и
и 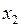 незначимы, так как для них P-значениябольше 0,05. В то же время сравнение расчетного значения
незначимы, так как для них P-значениябольше 0,05. В то же время сравнение расчетного значения 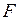 -критерия с табличным
-критерия с табличным  (2, 17) = 3,59 позволяет сделать вывод об адекватности рассматриваемой модели.
(2, 17) = 3,59 позволяет сделать вывод об адекватности рассматриваемой модели.
Коэффициенты корреляции говорят о существенной взаимосвязи моделируемого показателя с факторами (см. табл. 26, полученную в результате использования функции КОРРЕЛ). Одной из причин противоречивости результатов модели является тесная взаимосвязь между факторами. Все эти факты говорят о том, что изучаемая модель требует более детального анализа.
Т а б л и ц а 16
Корреляционная матрица

| 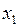
| 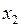
| |

| 0,9972 | 0,9971 | |
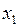
| 0,9972 | 0,9999 | |
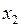
| 0,9971 | 0,9999 |
3. Проверка условия невырожденности матрицы  .
.
3.1. Формирование матрицы  с помощью функций ТРАНСП и МУМНОЖ
с помощью функций ТРАНСП и МУМНОЖ
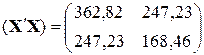 .
.
3.2. Вычисление определителя матрицы  с помощью функции МОПРЕД
с помощью функции МОПРЕД
 0,0633.
0,0633.
Близость определителя к нулю, а также проведенный выше анализ позволяют сделать вывод о наличии частичной мультиколлинеарности.
4. Устранение эффекта мультиколлинеарности с помощью ридж-оценивания.
4.1. Включение в модель дополнительной переменной  , принимающей единственное значение, равное 1.
, принимающей единственное значение, равное 1.
4.2. Расчет коэффициентов регрессии с использованием матричных функций Excel.
4.2.1. Формирование матрицы, обратной к матрице системы нормальных уравнений  с помощью функций ТРАНСП, МУМНОЖ и МОБР при
с помощью функций ТРАНСП, МУМНОЖ и МОБР при  .
.
 ;
;
 ;
;
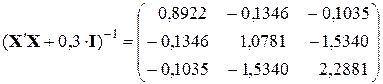 ;
;
 .
.
4.2.2. Получение вектора оценок коэффициентов регрессии путем умножения обратной матрицы на матрицы  и
и  при различных значениях
при различных значениях  . Оформление результатов виде табл. 17.
. Оформление результатов виде табл. 17.
Т а б л и ц а 17
Оценки коэффициентов регрессии при разных значениях 

| 
| 
| 
| |

| -0,0937 | -0,0745 | -0,0588 | -0,0458 |

| 0,4454 | 0,4411 | 0,4381 | 0,4358 |

| 0,2975 | 0,2972 | 0,2961 | 0,2950 |
5. Расчет стандартных ошибок коэффициентов регрессии.
5.1. Вычисление остаточной дисперсии при различных значениях  и оформление результатов расчетов в виде табл. 18.
и оформление результатов расчетов в виде табл. 18.
Т а б л и ц а 18
| Квадраты отклонений расчетных от фактических значений | |||

| 
| 
| 
|
| 0,001703 | 0,001766 | 0,001826 | 0,001884 |
| 0,000060 | 0,000028 | 0,000011 | 0,000003 |
| 0,002836 | 0,002686 | 0,002576 | 0,002493 |
| 0,000028 | 0,000024 | 0,000020 | 0,000016 |
| 0,002997 | 0,002993 | 0,002980 | 0,002961 |
| 0,003277 | 0,003036 | 0,002854 | 0,002715 |
| 0,000265 | 0,000489 | 0,000728 | 0,000970 |
| 0,000248 | 0,000139 | 0,000074 | 0,000037 |
| 0,000564 | 0,000336 | 0,000195 | 0,000109 |
| 0,003337 | 0,004280 | 0,005152 | 0,005956 |
| 0,002048 | 0,002051 | 0,002062 | 0,002078 |
| 0,004453 | 0,004163 | 0,003920 | 0,003714 |
| 0,000854 | 0,000599 | 0,000420 | 0,000292 |
| 0,002048 | 0,002051 | 0,002062 | 0,002078 |
| 0,005815 | 0,006670 | 0,007400 | 0,008024 |
| 0,000885 | 0,001211 | 0,001509 | 0,001776 |
| 0,001742 | 0,001989 | 0,002196 | 0,002368 |
| 0,000060 | 0,000028 | 0,000011 | 0,000003 |
Окончание табл. 18
| 0,001462 | 0,000980 | 0,000653 | 0,000426 |
| 0,001502 | 0,001733 | 0,001927 | 0,002090 |
| Сумма квадратов отклонений расчетных от фактических значений | |||
| 0,036183 | 0,037251 | 0,038577 | 0,039994 |
| Остаточная дисперсия | |||
| 0,002128 | 0,002191 | 0,002269 | 0,002353 |
5.2. Получение стандартных ошибок в виде корня квадратного из произведения диагональных элементов обратной матрицы на остаточную дисперсию при различных значениях  . Оформление результатов расчетов в виде табл. 19.
. Оформление результатов расчетов в виде табл. 19.
Т а б л и ц а 19
Стандартные ошибки коэффициентов регрессии при разных значениях 

| 
| 
| 
| |

| 0,0483 | 0,0464 | 0,0450 | 0,0438 |

| 0,0824 | 0,0593 | 0,0495 | 0,0437 |

| 0,1207 | 0,0867 | 0,0721 | 0,0636 |
Таким образом, наименьшая стандартная ошибка получена при  .Следовательно, построенная модель может быть записана в виде
.Следовательно, построенная модель может быть записана в виде
 .
.
6. Проверка значимости полученных коэффициентов регрессии
 ;
;  ;
; 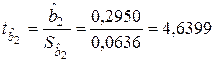 .
.
Сравнение расчетных значений t -статистик с табличным  свидетельствует о значимости включенных в модель факторов
свидетельствует о значимости включенных в модель факторов 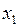 и
и 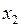 . Таким образом, построенную модель можно использовать для целей анализа и прогнозирования.
. Таким образом, построенную модель можно использовать для целей анализа и прогнозирования.
Задание 2. Начальник отдела маркетинга кинотеатра «Отражение» поручил своим сотрудникам провести исследование, в результате которого необходимо: 1) выявить фактор, в наибольшей степени влияющий на среднее число зрителей за первые три дня проката фильма; 2) построить прогнозную модель в виде линейной функции; 3) с помощью построенной модели получить прогнозные оценки среднего числа зрителей на первые три дня проката следующих двух фильмов. Специалисты отдела маркетинга экспертным путем в качестве фактора, в наибольшей степени влияющего на посещение киносеансов, установили расходы на рекламу фильма, (см. табл. 20). Выполните 2-е и 3-е задание начальника отдела маркетинга.
Т а б л и ц а 20
Показатели, характеризующие деятельность кинотеатра «Отражение»
| Среднее число зрителей за первые три дня проката фильма | Расходы на рекламу фильма, руб. | Среднее число зрителей за первые три дня проката фильма | Расходы на рекламу фильма, руб. |
Задание 3. Предприниматель желает сдать в аренду на один год принадлежащий ему отель*** «Блаженство жизни» (80 комнат), расположенный в престижной курортной зоне, обладающий собственным пляжем, общая площадь территории отеля составляет 3,42 кв.м.
Для того чтобы определить величину платы, которую он сможет установить за аренду своего отеля, предприниматель решил проанализировать ситуацию на соответствующей рыночной нише. Изучение объявлений, размещенных в газетах владельцами трехзвездных отелей, позволило ему сформировать небольшую базу данных, представленную в виде табл. 21.
Т а б л и ц а 21
Данные о трехзвездных отелях
| Величина годовой платы за аренду отеля, тыс. руб. | Число комнат в отеле | Престижность района, в котором расположен отель | Наличие у отеля собственного пляжа | Общая площадь территории, принадлежащей отелю, кв. км. | |
| 1,00 | |||||
| 0,80 | |||||
| 1,20 | |||||
| 1,50 | |||||
| 1,40 | |||||
| 2,00 | |||||
| 2,50 | |||||
| 2,20 | |||||
| 2,70 | |||||
| 2,80 | |||||
| 3,00 | |||||
| 3,60 |
Окончание табл. 21
| 3,50 | ||||
| 3,80 | ||||
| 3,60 | ||||
| 3,75 | ||||
| 4,10 | ||||
| 4,70 | ||||
| 4,25 | ||||
| 4,65 |
На основе данных этой базы предприниматель решил построить модель множественной регрессии, отражающую зависимость величины годовой арендной платы от числа комнат, престижности района расположения отеля (1 – престижный район, 0 – нет), наличия у отеля собственного пляжа (1 – есть собственный пляж, 0 – нет), а также общей площади территории, принадлежащей отелю, и с помощью построенной модели определить примерный размер платы, которую он может получать за предоставление в аренду своего отеля. На данный момент выбор предпринимателя колеблется между 162 тыс. руб. и 165 тыс. руб. Определите наиболее приемлемый размер арендной платы.
Зад
Date: 2016-02-19; view: 1247; Нарушение авторских прав