
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обобщенный регрессионный анализ
|
|
Пример 5. В табл. 23 представлены данные о потребительских расходах (у,у.е.) и располагаемом доходе (х,у.е.) тридцати семей. Проверьте эти данные на наличие гетероскедастичности, используя: 1) критерий Уайта; 2) критерий Бреуша – Пагана.
Т а б л и ц а 23
| № п.п. | у | х | № п.п. | у | х | № п.п. | у | х |
| 1. | 11. | 21. | ||||||
| 2. | 12. | 22. | ||||||
| 3. | 13. | 23. | ||||||
| 4. | 14. | 24. | ||||||
| 5. | 15. | 25. | ||||||
| 6. | 16. | 26. | ||||||
| 7. | 17. | 27. | ||||||
| 8. | 18. | 28. | ||||||
| 9. | 19. | 29. | ||||||
| 10. | 20. | 30. |
Решение с помощью табличного процессора Excel
1. Ввод исходных данных.
2. Построение регрессионного уравнения с помощью пакета анализа (см. Вывод итогов 6)
| ВЫВОД ИТОГОВ 6 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,984083 | |||||
| R-квадрат | 0,968419 | |||||
| Нормированный R-квадрат | 0,967291 | |||||
| Стандартная ошибка | 420,4049 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1,52E+08 | 1,52E+08 | 858,6118 | 1,49E-22 | ||
| Остаток | 176740,3 | |||||
| Итого | 1,57E+08 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 447,5552 | 3,530291 | 0,001457 | 663,2238 | 2496,776 | |
| Переменная X 1 | 0,78303 | 0,026723 | 29,30208 | 1,49E-22 | 0,728291 | 0,837769 |
3. Получение расчетных значений  и вычисление остатков
и вычисление остатков 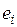 и
и 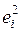 ,
,  . Оформление результатов расчетов в виде табл. 24.
. Оформление результатов расчетов в виде табл. 24.
Т а б л и ц а 24
| № п.п. | 
| 
| 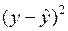
| № п.п. | 
| 
| 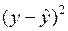
|
| 1. | 10976,36 | 76376,86 | 16. | 14891,52 | 71,99 | ||
| 2. | 11759,39 | 129164,00 | 17. | 15674,55 | 647,93 | ||
| 3. | 12542,42 | 58769,51 | 18. | 16457,58 | 1799,82 | ||
| 4. | 13325,45 | 105920,66 | 19. | 17240,61 | 67285,22 | ||
| 5. | 14108,48 | 95162,90 | 20. | 18023,64 | 50013,22 | ||
| 6. | 14891,52 | 241587,14 | 21. | 10976,36 | 50013,22 | ||
| 7. | 15674,55 | 455011,57 | 22. | 11759,39 | 116012,49 | ||
| 8. | 16457,58 | 310890,73 | 23. | 12542,42 | 432405,88 | ||
| 9. | 17240,61 | 116012,49 | 24. | 13325,45 | 75375,21 | ||
| 10. | 18023,64 | 678376,86 | 25. | 14108,48 | 8375,02 | ||
| 11. | 10976,36 | 5831,40 | 26. | 14891,52 | 166859,87 | ||
| 12. | 11759,39 | 3527,64 | 27. | 15674,55 | 526284,30 | ||
| 13. | 12542,42 | 3314,97 | 28. | 16457,58 | 195739,21 | ||
| 14. | 13325,45 | 647,93 | 29. | 17240,61 | 738557,94 | ||
| 15. | 14108,48 | 11768,96 | 30. | 18023,64 | 226922,31 |
4. Построение графика квадратов остатков (см. рис. 12). График зависимости квадратов остатков регрессии от независимой переменной имеет вид, вынуждающий предполагать гетероскедастичность.
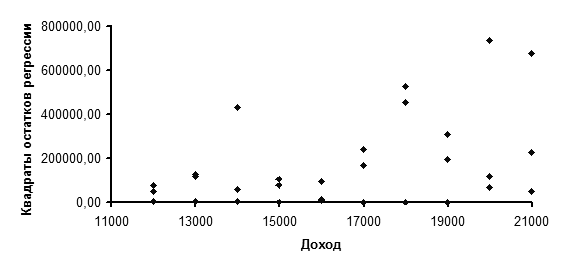
Р и с. 12. График зависимости квадратов остатков от величины дохода
5. Проверка данных с помощью теста Уайта.
5.1. Вычисление 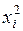 и построение регрессионного уравнения (см. Вывод итогов 7)
и построение регрессионного уравнения (см. Вывод итогов 7)  .
.
5.2. Расчет  и сравнение этой величины с критическим значением
и сравнение этой величины с критическим значением 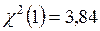 . Результаты сравнения позволяют отвергнуть нуль-гипотезу (отсутствие гетероскедастичности).
. Результаты сравнения позволяют отвергнуть нуль-гипотезу (отсутствие гетероскедастичности).
| ВЫВОД ИТОГОВ 7 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,440291 | |||||
| R-квадрат | 0,193856 | |||||
| Нормированный R-квадрат | 0,134142 | |||||
| Стандартная ошибка | 190982,8 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 2,37E+11 | 1,18E+11 | 3,246397 | 0,054521 | ||
| Остаток | 9,85E+11 | 3,65E+10 | ||||
| Итого | 1,22E+12 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 427676,8 | 0,333329 | 0,741461 | -2204919 | ||
| Переменная X 1 | -64,7853 | 158,8192 | -0,40792 | 0,68655 | -390,655 | 261,0846 |
| Переменная X 2 | 0,002874 | 0,004799 | 0,598982 | 0,554178 | -0,00697 | 0,01272 |
6. Проверка данных с помощью теста Бреуша – Пагана.
6.1. Вычисление оценки дисперсии
 .
.
6.2. Расчет  и построение регрессионного уравнения (см. Вывод итогов 8)
и построение регрессионного уравнения (см. Вывод итогов 8) 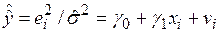 .
.
| ВЫВОД ИТОГОВ 8 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,427954 | |||||
| R-квадрат | 0,183144 | |||||
| Нормированный R-квадрат | 0,153971 | |||||
| Стандартная ошибка | 1,144436 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 8,222216 | 8,222216 | 6,27778 | 0,018316 | ||
| Остаток | 36,67252 | 1,309733 | ||||
| Итого | 44,89474 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -2,0074 | 1,218345 | -1,64764 | 0,110604 | -4,50307 | 0,488272 |
| Переменная X 1 | 0,000182 | 7,27E-05 | 2,50555 | 0,018316 | 3,33E-05 | 0,000331 |
6.3. Вычисление среднего, расчетных значений, квадратов отклонений расчетных значений от среднего и ESS как суммы квадратов этих отклонений. Оформление результатов расчетов в виде табл. 25.
Т а б л и ц а 25
| № п.п. | 
| 
| 
| 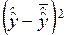
| № п.п. | 
| 
| 
| 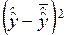
|
| 1. | 0,4630 | 0,1798 | 0,6727 | 16. | 0,0004 | 1,0911 | 0,0083 | ||
| 2. | 0,7830 | 0,3621 | 0,4070 | 17. | 0,0039 | 1,2734 | 0,0747 | ||
| 3. | 0,3563 | 0,5443 | 0,2076 | 18. | 0,0109 | 1,4557 | 0,2076 | ||
| 4. | 0,6421 | 0,7266 | 0,0747 | 19. | 0,4079 | 1,6379 | 0,4070 | ||
| 5. | 0,5769 | 0,9089 | 0,0083 | 20. | 0,3032 | 1,8202 | 0,6727 | ||
| 6. | 1,4645 | 1,0911 | 0,0083 | 21. | 0,3032 | 0,1798 | 0,6727 | ||
| 7. | 2,7584 | 1,2734 | 0,0747 | 22. | 0,7033 | 0,3621 | 0,4070 | ||
| 8. | 1,8847 | 1,4557 | 0,2076 | 23. | 2,6213 | 0,5443 | 0,2076 | ||
| 9. | 0,7033 | 1,6379 | 0,4070 | 24. | 0,4569 | 0,7266 | 0,0747 | ||
| 10. | 4,1124 | 1,8202 | 0,6727 | 25. | 0,0508 | 0,9089 | 0,0083 | ||
| 11. | 0,0354 | 0,1798 | 0,6727 | 26. | 1,0115 | 1,0911 | 0,0083 | ||
| 12. | 0,0214 | 0,3621 | 0,4070 | 27. | 3,1904 | 1,2734 | 0,0747 | ||
| 13. | 0,0201 | 0,5443 | 0,2076 | 28. | 1,1866 | 1,4557 | 0,2076 | ||
| 14. | 0,0039 | 0,7266 | 0,0747 | 29. | 4,4773 | 1,6379 | 0,4070 | ||
| 15. | 0,0713 | 0,9089 | 0,0083 | 30. | 1,3756 | 1,8202 | 0,6727 | ||
| СРЗНАЧ | ESS | ||||||||
| 1,0000 | 8,2222 |
6.4. Вычисление статистики ESS/2 = 8,22/2 = 4,11. При нулевой гипотезе отсутствия гетероскедастичности эта статистика имеет распределение  , 95%-критическое значение которой равно 3,84. Поскольку 4,11 > 3,84, гипотеза о гомоскедастичности отвергается.
, 95%-критическое значение которой равно 3,84. Поскольку 4,11 > 3,84, гипотеза о гомоскедастичности отвергается.
Пример 6. По данным табл. 26 постройте линейную регрессионную модель, характеризующую зависимость показателя  от факторов
от факторов  и
и 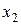 .
.
Т а б л и ц а 26
| № | 
| 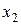
| 
| № | 
| 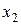
| 
|
| 1. | 11. | ||||||
| 2. | 12. | ||||||
| 3. | 13. | ||||||
| 4. | 14. | ||||||
| 5. | 15. | ||||||
| 6. | 16. | ||||||
| 7. | 17. | ||||||
| 8. | 18. | ||||||
| 9. | 19. | ||||||
| 10. | 20. |
Построение модели следует начать с тестирования на гетероскедастичность. Считая наиболее вероятной ситуацию с двухуровневой дисперсией, используйте для проверки тест Голдфельда – Куандта. Если проверкой будет установлена неоднородность данных, то при построении модели примените многоэтапную процедуру оценивания ее коэффициентов с помощью доступного МНК. Получите прогнозную оценку  на следующий период при условии, что
на следующий период при условии, что  ,
,  .
.
Решение с помощью MS Excel
1. Ввод исходных данных.
2. Проверка данных с помощью теста Голдфельда – Куандта.
2.1. Упорядочивание исходных данных по переменной  в предположении, что уровень дисперсии зависит от этой переменной, и удаление шести наблюдений, оказавшихся в середине выборки. Представление результатов в виде табл. 27.
в предположении, что уровень дисперсии зависит от этой переменной, и удаление шести наблюдений, оказавшихся в середине выборки. Представление результатов в виде табл. 27.
Т а б л и ц а 27
| № | 
| 
| 
| № | 
| 
| 
|
| 1. | 14. | ||||||
| 2. | 15. | ||||||
| 3. | 16. | ||||||
| 4. | 17. | ||||||
| 5. | 18. | ||||||
| 6. | 19. | ||||||
| 7. | 20. |
2.2. Построение по упорядоченным данным двух регрессионных уравнений по первым семи наблюдениям (первое регрессионное уравнение, см. Вывод итогов 9) и по последним семи наблюдениям (второе регрессионное уравнение, см. Вывод итогов 10).
| ВЫВОД ИТОГОВ 9 | |||||||
| Регрессионная статистика | |||||||
| Множественный R | 0,965091 | ||||||
| R-квадрат | 0,931401 | ||||||
| Нормированный R-квадрат | 0,897101 | ||||||
| Стандартная ошибка | 16,65463 | ||||||
| Наблюдения | |||||||
| Дисперсионный анализ | |||||||
| df | SS | MS | F | Значимость F | |||
| Регрессия | 15064,2081 | 7532,104 | 27,1548 | 0,0047059 | |||
| Остаток | 1109,50616 | 277,3765 | |||||
| Итого | 16173,7143 | ||||||
| Коэффициенты | Стандартная ошибка | t-статис- тика | P-Значение | Нижние 95% | Верхние 95% | ||
| Y-пересечение | 13,86422 | 26,6435024 | 0,52036 | 0,630286 | -60,11015 | 87,838598 | |
| Переменная X 1 | 0,889493 | 0,39236032 | 2,267031 | 0,086009 | -0,199876 | 1,978862 | |
| Переменная X 2 | 0,89948 | 0,13496104 | 6,66474 | 0,002633 | 0,5247676 | 1,274193 |
| ВЫВОД ИТОГОВ 10 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,99412 | |||||
| R-квадрат | 0,988274 | |||||
| Нормированный R-квадрат | 0,982411 | |||||
| Стандартная ошибка | 5,576546 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 10483,6085 | 5241,804 | 168,5583 | 0,000138 | ||
| Остаток | 124,391476 | 31,09787 | ||||
| Итого | ||||||
| Коэффициенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 23,49446 | 6,3630766 | 3,692312 | 0,020976 | 5,827693 | 41,161232 |
| Переменная X 1 | 1,476582 | 0,11317714 | 13,04665 | 0,000199 | 1,162351 | 1,7908128 |
| Переменная X 2 | 0,826054 | 0,07856709 | 10,51399 | 0,000463 | 0,607916 | 1,0441916 |
2.3. Получение расчетных значений и вычисление остатков 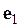 и
и  , с помощью которых составляется статистика
, с помощью которых составляется статистика  . Оформление результатов в виде табл. 28.
. Оформление результатов в виде табл. 28.
Т а б л и ц а 28
| № | 
| 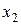
| 
| 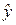
| 
|
| 1. | 304,97 | 36,41 | |||
| 2. | 202,65 | 385,93 | |||
| 3. | 213,25 | 85,55 | |||
| 4. | 182,85 | 447,46 | |||
| 5. | 210,27 | 10,70 | |||
| 6. | 167,42 | 112,03 | |||
| 7. | 149,61 | 31,43 | |||
 =1109,51 =1109,51
| |||||
| 14. | 166,46 | 20,57 | |||
| 15. | 132,98 | 24,78 | |||
| 16. | 196,42 | 6,66 | |||
| 17. | 111,10 | 1,21 | |||
| 18. | 78,21 | 0,62 | |||
| 19. | 146,78 | 46,02 | |||
| 20. | 92,05 | 24,53 | |||
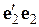 =124,39 =124,39
|
 ;
; 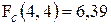 .
.
Так как 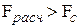 , то гипотеза
, то гипотеза  отвергается и, следовательно, в данных наблюдается гетероскедастичность с двухуровневой дисперсией. Поэтому для построения регрессии по данным табл. 36 необходимо применить многоэтапную процедуру доступного МНК.
отвергается и, следовательно, в данных наблюдается гетероскедастичность с двухуровневой дисперсией. Поэтому для построения регрессии по данным табл. 36 необходимо применить многоэтапную процедуру доступного МНК.
3. Построение регрессии с помощью доступного взвешенного МНК.
3.1. Построение регрессии обычным МНК по данным табл. 27 (см. Вывод итогов 11).
| ВЫВОД ИТОГОВ 11 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,968969836 | |||||
| R-квадрат | 0,938902544 | |||||
| Нормированный R-квадрат | 0,931714608 | |||||
| Стандартная ошибка | 13,07464604 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 44658,7117 | 22329,36 | 130,622 | 4,8E-11 | ||
| Остаток | 2906,08827 | 170,9464 | ||||
| Итого | 47564,8 | |||||
| Коэффициенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 36,78068243 | 9,43676522 | 3,897594 | 0,001158 | 16,87082 | 56,690545 |
| Переменная X 1 | 1,191842832 | 0,16975113 | 7,021119 | 2,06E-06 | 0,833699 | 1,5499869 |
| Переменная X 2 | 0,760391162 | 0,04869436 | 15,61559 | 1,63E-11 | 0,657655 | 0,8631274 |
3.2. Получение расчетных оценок 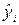 и вычисление абсолютных значений отклонений. Оформление результатов в виде табл. 29.
и вычисление абсолютных значений отклонений. Оформление результатов в виде табл. 29.
Т а б л и ц а 29
| № | 
| 
| 
| 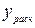
| 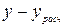
| 
|
| 1. | 84,971 | -5,971 | 5,971 | |||
| 2. | 112,734 | -2,734 | 2,734 | |||
| 3. | 94,361 | 2,639 | 2,639 | |||
| 4. | 161,356 | 9,644 | 9,644 | |||
| 5. | 184,912 | 19,088 | 19,088 | |||
| 6. | 183,510 | -9,510 | 9,510 | |||
| 7. | 178,538 | 5,462 | 5,462 | |||
| 8. | 297,385 | 13,615 | 13,615 | |||
| 9. | 184,518 | 21,482 | 21,482 | |||
| 10. | 134,047 | -6,047 | 6,047 | |||
| 11. | 228,331 | -21,331 | 21,331 | |||
| 12. | 146,315 | 5,685 | 5,685 |
Окончание табл. 29
| 13. | 184,411 | 14,589 | 14,589 | |||
| 14. | 155,051 | -11,051 | 11,051 | |||
| 15. | 140,228 | -0,228 | 0,228 | |||
| 16. | 201,209 | -18,209 | 18,209 | |||
| 17. | 178,025 | -0,025 | 0,025 | |||
| 18. | 196,928 | -11,928 | 11,928 | |||
| 19. | 142,637 | 9,363 | 9,363 | |||
| 20. | 218,531 | -14,531 | 14,531 |
3.3. Деление наблюдений с помощью Автофильтра на две группы  и
и  со значениями остатков, по абсолютной величине превосходящих и не превосходящих заданный уровень. (Анализ последнего столбца табл. 29 позволил в качестве такого уровня выбрать 7.)
со значениями остатков, по абсолютной величине превосходящих и не превосходящих заданный уровень. (Анализ последнего столбца табл. 29 позволил в качестве такого уровня выбрать 7.)
3.4. Расчет среднеквадратических ошибок по остаткам, не превосходящих заданный уровень, и среднеквадратических ошибок по остаткам, превосходящих заданный уровень.
 ;
; 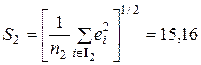 .
.
3.5. Преобразование исходных данных путем деления зависимой и независимых переменных каждого наблюдения первой группы на 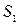 , а второй группы – на
, а второй группы – на  и оформление результатов в виде табл. 30.
и оформление результатов в виде табл. 30.
Т а б л и ц а 30
| № | 
| 
| 
| 
| 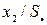
| 
|
| 1. | 3,014 | 9,968 | 18,314 | |||
| 2. | 6,491 | 12,982 | 25,500 | |||
| 3. | 7,650 | 5,564 | 22,487 | |||
| 4. | 2,771 | 6,465 | 11,281 | |||
| 5. | 0,792 | 11,611 | 13,458 | |||
| 6. | 2,903 | 8,180 | 11,479 | |||
| 7. | 8,346 | 30,137 | 42,655 | |||
| 8. | 2,177 | 19,198 | 20,517 | |||
| 9. | 2,243 | 9,302 | 13,590 | |||
| 10. | 4,868 | 22,023 | 29,673 | |||
| 11. | 3,826 | 10,621 | 13,656 | |||
| 12. | 5,332 | 25,037 | 35,237 | |||
| 13. | 4,552 | 5,674 | 13,128 | |||
| 14. | 0,528 | 9,434 | 9,500 | |||
| 15. | 13,909 | 9,736 | 32,455 | |||
| 16. | 0,726 | 13,128 | 12,073 | |||
| 17. | 6,027 | 33,614 | 41,264 | |||
| 18. | 4,024 | 7,587 | 12,205 | |||
| 19. | 1,187 | 7,323 | 10,028 | |||
| 20. | 1,979 | 12,666 | 13,458 |
3.6. Построение регрессионной модели по преобразованным данным табл. 30. Использование преобразованных данных для построения регрессионной модели эквивалентно применению взвешенного МНК к исходным данным (см. Вывод итогов 12).
| ВЫВОД ИТОГОВ 12 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,985102 | |||||
| R-квадрат | 0,970425 | |||||
| Нормированный R-квадрат | 0,966946 | |||||
| Стандартная ошибка | 1,948194 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 2117,1754 | 1058,588 | 278,9088 | 1,01E-13 | ||
| Остаток | 64,5228463 | 3,795462 | ||||
| Итого | 2181,69825 | |||||
| Коэффициенты | Стандартная ошибка | t-статис-тика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 0,148364 | 0,95183574 | 0,155871 | 0,877971 | -1,85984 | 2,1565644 |
| Переменная X 1 | 1,818385 | 0,14250896 | 12,75979 | 3,91E-10 | 1,517717 | 2,1190528 |
| Переменная X 2 | 0,915585 | 0,05632975 | 16,25403 | 8,6E-12 | 0,79674 | 1,034431 |
Таким образом, уравнение регрессии, построенное с учетом гетероскедастичности, имеет вид
 .
.
3.7. Получение прогнозной оценки моделируемого показателя
 .
.
Задание 5. Проверьте данные, представленные в табл. 31, на наличие гетероскедастичности, используя тест: 1) Уайта; 2) Бреуша – Пагана.
Т а б л и ц а 31
| № п.п. | 
| 
| № п.п. | 
| 
|
| 1. | 10,00 | 110,00 | 11. | 15,00 | 111,64 |
| 2. | 10,50 | 110,66 | 12. | 15,50 | 119,65 |
| 3. | 11,00 | 110,06 | 13. | 16,00 | 126,36 |
| 4. | 11,50 | 112,83 | 14. | 16,50 | 125,12 |
| 5. | 12,00 | 112,92 | 15. | 17,00 | 121,76 |
| 6. | 12,50 | 113,17 | 16. | 17,50 | 125,98 |
| 7. | 13,00 | 108,35 | 17. | 18,00 | 122,87 |
| 8. | 13,50 | 120,18 | 18. | 18,50 | 117,34 |
| 9. | 14,00 | 115,07 | 19. | 19,00 | 109,94 |
| 10. | 14,50 | 117,08 | 20. | 19,50 | 120,50 |
Задание 6. В табл. 32 приведены числовые данные о государственных расходах на образование (y, млрд. у.е.) и валовом внутреннем продукте (х, млрд. у.е.) для 34 стран. Проверьте эти данные на наличие гетероскедастичности, используя критерий Гольдфельда – Куандта. В случае подтверждения гипотезы о присутствии гетероскедастичности примените для построения модели, отражающей зависимость расходов на образование от ВВП, взвешенный метод наименьших квадратов.
Т а б л и ц а 32
| № | у | х | № | у | х |
| 1. | 0,34 | 5,67 | 18. | 5,31 | 101,65 |
| 2. | 0,22 | 10,13 | 19. | 6,40 | 115,97 |
| 3. | 0,32 | 11,34 | 20. | 7,15 | 119,49 |
| 4. | 1,23 | 18,88 | 21. | 11,22 | 124,15 |
| 5. | 1,81 | 20,94 | 22. | 8,66 | 140,98 |
| 6. | 1,02 | 22,16 | 23. | 5,56 | 153,85 |
| 7. | 1,27 | 23,83 | 24. | 13,41 | 169,38 |
| 8. | 1,07 | 24,67 | 25. | 5,46 | 186,33 |
| 9. | 0,67 | 27,56 | 26. | 4,79 | 211,78 |
| 10. | 1,25 | 27,57 | 27. | 8,92 | 249,72 |
| 11. | 0,75 | 40,15 | 28. | 18,90 | 261,41 |
| 12. | 2,80 | 51,62 | 29. | 15,95 | 395,52 |
| 13. | 4,90 | 57,71 | 30. | 29,90 | 534,97 |
| 14. | 3,50 | 63,03 | 31. | 33,59 | 655,29 |
| 15. | 4,45 | 66,32 | 32. | 38,62 | 815,00 |
| 16. | 1,60 | 66,97 | 33. | 61,61 | 1040,45 |
| 17. | 4,26 | 76,88 | 34. | 181,30 | 2586,40 |
Date: 2016-02-19; view: 637; Нарушение авторских прав