Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Прогнозирование сезонных колебаний
|
|
Пример 15. Требуетсяпостроить для прогнозирования пассажироотока Юго-Восточной железной дороги. Условные данные для расчетов приведены в табл. 59. Заметим, что график (см. рис. 42) свидетельствует о наличии слабо возрастающего тренда и аддитивной сезонной компоненты.
Т а б л и ц а 59
Пассажиропоток ЮВЖД (чел.)
| Период | Г о д | |||||
| Январь – февраль | ||||||
| Март – апрель | ||||||
| Май – июнь | ||||||
| Июль – август | ||||||
| Сентябрь – октябрь | ||||||
| Ноябрь – декабрь |
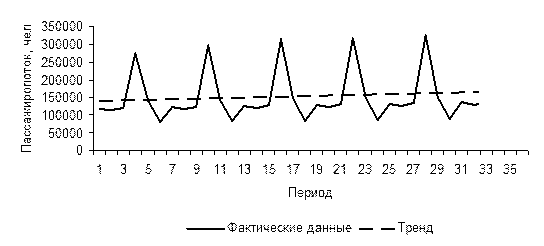
Рис. 42. Динамика пассажиропотока
Решение в Excel
1. Ввод исходных данных и оформление их в виде таблицы, удобной для расчета оценок сезонной компоненты.
2. Расчет оценок сезонной компоненты для аддитивной модели.
2.1. Расчет скользящих средних.
2.2. Вычисление сезонной компоненты в виде разницы фактических значений и скользящих средних.
2.3. Оформление результатов расчетов в виде табл. 60.
Т а б л и ц а 60
Расчет оценок сезонной компоненты в аддитивной модели
| Год | Период | Фактические данные | Скользящая средняя | Оценка сезонной компоненты |
| Январь – февраль | – | – | ||
| Март – апрель | – | – | ||
| Май – июнь | – | – |
Окончание табл. 60
| Июль – август | 141819,3 | 133914,7 | ||
| Сентябрь – октябрь | 142433,7 | -3115,7 | ||
| Ноябрь – декабрь | 142658,0 | -61658,0 | ||
| Январь – февраль | 143140,3 | -21091,3 | ||
| Март – апрель | 146660,7 | -30062,7 | ||
| Май – июнь | 147228,0 | -23085,0 | ||
| Июль – август | 147664,0 | 149192,0 | ||
| Сентябрь – октябрь | 148410,7 | -5688,7 | ||
| Ноябрь – декабрь | 149276,2 | -65660,2 | ||
| Январь – февраль | 150156,5 | -23627,5 | ||
| Март – апрель | 152825,8 | -31034,8 | ||
| Май – июнь | 153542,8 | -24117,8 | ||
| Июль – август | 153790,3 | 159081,7 | ||
| Сентябрь – октябрь | 154080,8 | -7056,8 | ||
| Ноябрь – декабрь | 154544,5 | -69443,5 | ||
| Январь – февраль | 154824,7 | -26552,7 | ||
| Март – апрель | 155396,8 | -30823,8 | ||
| Май – июнь | 155564,0 | -24458,0 | ||
| Июль – август | 156062,3 | 160242,7 | ||
| Сентябрь – октябрь | 156597,0 | -8570,0 | ||
| Ноябрь – декабрь | 156792,8 | -68701,8 | ||
| Январь – февраль | 157127,0 | -25647,0 | ||
| Март – апрель | 158671,0 | -32923,0 | ||
| Май – июнь | 159390,8 | -26279,8 | ||
| Июль – август | 159573,8 | 165995,2 | ||
| Сентябрь – октябрь | 160478,7 | -8132,7 | ||
| Ноябрь – декабрь | 160871,0 | -71682,0 | ||
| Январь – февраль | 161759,5 | -24850,5 | ||
| Март – апрель | 162158,0 | -34056,0 | ||
| Май – июнь | 163229,3 | -24787,3 | ||
| Июль – август | 164515,5 | 163444,5 | ||
| Сентябрь – октябрь | – | – | ||
| Ноябрь – декабрь | – | – |
3. Расчет средних значений сезонной компоненты аддитивной модели.
3.1. Формирование из оценок сезонной компоненты, полученных в предыдущем пункте, табл. 61, удобной для расчета средних значений этой же компоненты.
3.2. Расчет итоговых значений сезонной компоненты.
3.3. Определение средних значений итоговой компоненты.
3.4. Определение корректирующего коэффициента
.
3.5. Расчет скорректированных значений сезонной компоненты путем вычитания корректирующего коэффициента из средних оценок сезонной компоненты (сумма скорректированных значений равна нулю).
Т а б л и ц а 61
Расчет значений сезонной компоненты в аддитивной модели
| Показатель | Год | Номер периода | |||||
| – | – | – | 133914,7 | -3115,7 | -61658,0 | ||
| -21091,3 | -30062,7 | -23085,0 | 149192,0 | -5688,7 | -65660,2 | ||
| -23627,5 | -31034,8 | -24117,8 | 159081,7 | -7056,8 | -69443,5 | ||
| -26552,7 | -30823,8 | -24458,0 | 160242,7 | -8570,0 | -68701,8 | ||
| -25647,0 | -32923,0 | -26279,8 | 165995,2 | -8132,67 | -71682,0 | ||
| -24850,5 | -34056,0 | -24787,3 | 163444,5 | – | – | ||
| Итого за период (за все годы) | -121769,0 | -158900 | -122728,0 | 931870,7 | -32563,8 | -337146 | |
| Средняя оценка сезонной компоненты | -24353,8 | -31780,1 | -24545,6 | 155311,8 | -6512,7 | -67429,1 | |
| Скорректированная сезонная компонента | -24468,9 | -31895,1 | -24660,7 | 155196,7 | -6627,8 | -67544,2 |
4. Вычисление основных составляющих сезонной модели.
4.1. Элиминирование влияния сезонной компоненты путем вычитания ее значения из каждого уровня исходного временного ряда.
4.2. Построение по данным элиминированного временного ряда трендовой модели с помощью МНК (см. Вывод итогов 15).
| ВЫВОД ИТОГОВ 15 | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,823671 | |||||
| R-квадрат | 0,678433 | |||||
| Нормированный R-квадрат | 0,668976 | |||||
| Стандартная ошибка | 5265,595 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1,99E+09 | 1,99E+09 | 71,73237 | 6,84E-10 | ||
| Остаток | 9,43E+08 | |||||
| Итого | 2,93E+09 | |||||
| Коэффи-циенты | Стандартная ошибка | t-статис-тика | P-Зна-чение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 140667,5 | 1792,415 | 78,4793 | 5,09E-40 | 137024,9 | 144310,1 |
| Переменная X 1 | 715,4998 | 84,47961 | 8,469497 | 6,84E-10 | 543,8167 | 887,1829 |
4.3. Получение расчетных значений по трендовой модели
.
4.4. Расчет значений уровня ряда по аддитивной модели.
4.5. Оформление результатов расчетов в виде табл. 62.
Т а б л и ц а 62
Расчетные значения аддитивной тренд-сезонной модели
| Пассажиро-
поток,
| Сезонная
компонента,
| Десезонали-зированный пассажиропоток,
| Расчетные значения (линейный тренд) 
| Расчетные
значения пассажиропотока
|
| -24468,9 | 142831,9 | 141383,0 | 116914,1 | ||
| -31895,1 | 147147,1 | 142098,5 | 110203,3 | ||
| -24660,7 | 145909,7 | 142814,0 | 118153,3 | ||
| 155196,7 | 120537,3 | 143529,5 | 298726,2 | ||
| -6627,8 | 145945,8 | 144245,0 | 137617,1 | ||
| -67544,2 | 148544,2 | 144960,5 | 77416,3 | ||
| -24468,9 | 146517,9 | 145676,0 | 121207,1 | ||
| -31895,1 | 148493,1 | 146391,5 | 114496,3 | ||
| -24660,7 | 148803,7 | 147107,0 | 122446,3 | ||
| 155196,7 | 141659,3 | 147822,5 | 303019,2 | ||
| -6627,8 | 149349,8 | 148538,0 | 141910,1 | ||
| -67544,2 | 151160,2 | 149253,5 | 81709,3 | ||
| -24468,9 | 150997,9 | 149969,0 | 125500,1 | ||
| -31895,1 | 153686,1 | 150684,5 | 118789,3 | ||
| -24660,7 | 154085,7 | 151400,0 | 126739,3 | ||
| 155196,7 | 157675,3 | 152115,5 | 307312,2 | ||
| -6627,8 | 153651,8 | 152831,0 | 146203,1 | ||
| -67544,2 | 152645,2 | 153546,5 | 86002,3 | ||
| -24468,9 | 152740,9 | 154262,0 | 129793,1 | ||
| -31895,1 | 156468,1 | 154977,5 | 123082,3 | ||
| -24660,7 | 155766,7 | 155693,0 | 131032,3 | ||
| 155196,7 | 161108,3 | 156408,5 | 311605,2 | ||
| -6627,8 | 154654,8 | 157124,0 | 150496,1 | ||
| -67544,2 | 155635,2 | 157839,5 | 90295,3 | ||
| -24468,9 | 155948,9 | 158555,0 | 134086,1 | ||
| -31895,1 | 157643,1 | 159270,5 | 127375,3 | ||
| -24660,7 | 157771,7 | 159986,0 | 135325,3 | ||
| 155196,7 | 170372,3 | 160701,5 | 315898,2 | ||
| -6627,8 | 158973,8 | 161417,0 | 154789,1 | ||
| -67544,2 | 156733,2 | 162132,5 | 94588,3 | ||
| -24468,9 | 161377,9 | 162848,0 | 138379,1 | ||
| -31895,1 | 159997,1 | 163563,5 | 131668,3 | ||
| -24660,7 | 163102,7 | 164279,0 | 139618,3 | ||
| 155196,7 | 172763,3 | 164994,5 | 320191,2 | ||
| -6627,8 | 165401,8 | 165710,0 | 159082,1 | ||
| -67544,2 | 164450,2 | 166425,5 | 98881,3 |
5. Оценка качества построенной модели.
5.1. Расчет суммы квадратов отклонений фактических значений пассажиропотока от среднего значения.
5.2. Расчет суммы квадратов отклонений расчетных от фактических значений пассажиропотока.
5.3. Оформление результатов расчетов в виде табл. 63.
Т а б л и ц а 63
Расчет квадратов отклонений
|
|
| 
| 
|
| 1263178477,0 | 2099305,7 | ||
| 1493994282,7 | 25489018,1 | ||
| 1066363538,4 | 9583349,4 | ||
| 14842494753,4 | 528640296,8 | ||
| 212757878,7 | 2892943,9 | ||
| 5315025617,8 | 12842899,7 | ||
| 1014755182,8 | 708794,6 | ||
| 1391754216,5 | 4417001,1 | ||
| 885730348,2 | 2878790,3 | ||
| 20435210769,8 | 37984760,0 | ||
| 125042093,8 | 659127,9 | ||
| 4940434183,2 | 3635506,6 | ||
| 749402791,7 | 1058636,6 | ||
| 1031259041,5 | 9010008,1 | ||
| 599232320,6 | 7212990,4 | ||
| 25270754371,6 | 30911637,8 | ||
| 47337457,8 | 673824,6 | ||
| 4733883388,2 | 812338,5 | ||
| 657010816,0 | 2313739,3 | ||
| 860320597,0 | 2222093,6 | ||
| 519758936,5 | 5432,0 | ||
| 26374012622,8 | 22088353,4 | ||
| 34541741,0 | 6096605,5 | ||
| 4331380219,3 | 4858925,1 | ||
| 502845742,3 | 6791740,3 | ||
| 792772849,8 | 2648202,5 | ||
| 432358090,4 | 4903108,2 | ||
| 29468795929,5 | 93524877,7 | ||
| 2428056,5 | 5968880,4 | ||
| 4188059987,3 | 29152393,9 | ||
| 288837578,4 | 2161180,7 | ||
| 665754671,6 | 12718699,6 | ||
| 239080316,0 | 1383670,0 | ||
| 30295413777,8 | 60354679,2 | ||
| 23714735,6 | 94942,8 | ||
| 3248797336,5 | 3901787,9 | ||
| Сумма: | 188344494718,2 | 942700542,1 |
5.4. Расчет величины по формуле
.
Таким образом, аддитивная модель объясняет 99 % общей вариации уровней временного ряда пассажиропотока за рассматриваемый промежуток времени.
6. Расчет прогнозных значений для каждого сезонного периода 2006 г. и оформление результатов в виде табл. 64.
Т а б л и ц а 64
Прогнозирование пассажиропотока, чел.
| Год | Период | Прогнозные значения тренда | Сезонная компонента | Прогнозные значения пассажиропотока |
| Январь – февраль | -24469 | |||
| Март – апрель | -31895 | |||
| Май – июнь | -24661 | |||
| Июль – август | ||||
| Сентябрь – октябрь | -6628 | |||
| Ноябрь – декабрь | -67544 |
7. Построение графика (рис. 43), отражающего динамику пассажиропотока
Рис. 43. Прогнозная динамика пассажиропотока ЮВЖД
Сезонная декомпозиция в STATISTICA
11. Ввод исходных данных.
12. Вызов модуля «Прогноз/Серия времени» (Статистика / Дополнительные Линейные/Нелинейные модели / Прогноз/Серия времени).
13. Выбор переменных для анализа (Variables / Var1).
14. Переход в окно Seasonal Decomposition (Census 1)/Advance – Сезонная декомпозиция/ Дополнительно, см. рис. 44. Здесь необходимо сделать показанные на рисунке установки: Seasonal model – Additive (Сезонная модель – аддитивная); Seasonal lag (Сезонный лаг, т.е. длина сезонного периода) – 6; Number of backups per variable (Число дублирований каждой переменной) – 6.
Рис. 44. Окно Seasonal Decomposition (Census 1) – Сезонная декомпозиция
15. Выбор опции Summary: Seasonal decomposition (Результаты сезонной декомпозиции), появится таблица, представленная на рис. 48. В данной таблице содержатся: Var 1 – фактические данные; Moving Averages – скользящие средние; Diffrncs – разности; Seasonal Factors – сезонная составляющая; Adjusted Series – ряд, скорректированный на сезонную составляющую; Smoothed Trend-c. – сглаженная тренд-циклическая компонента (рассчитывается как взвешенная скользящая средняя (с весами 
) ряда, скорректированного на сезонную составляющую); Irreg. Compon. – нерегулярная составляющая (получается как разность между значениями ряда, скорректированного на сезонную составляющую, и значениями сглаженной тренд-циклической компоненты).
Рис. 45. Окно Seasonal decomposition: Additive season
(Сезонная декомпозиция: Аддитивная модель)
Пример 16. Известно, что стоимость репетиторских услуг зависит от спроса на такие услуги, который распределен по периодам подготовки к вступительным экзаменам по математике. Условно можно выделить четыре периода: 1) август – октябрь (низкая стоимость); 2) ноябрь – декабрь (средняя стоимость); 3) январь – март (стоимость выше средней); апрель – июль (высокая стоимость). Усредненные значения стоимости репетиторских услуг в г. Воронеже за шесть лет с разбивкой по указанным периодам приведены в табл. 65. Абитуриенты решили построить модель сезонных колебаний для расчета ожидаемой стоимости репетиторских услуг в 2006 г. Построенный ими график на рис. 46 свидетельствует о наличии сезонных колебаний с лагом, равным четырем, с общей тенденцией роста стоимости репетиторских услуг и увеличением амплитуды колебаний. Поскольку амплитуда сезонных колебаний увеличивается, то целесообразно для данного ряда строить мультипликативную модель.
Date: 2016-02-19; view: 686; Нарушение авторских прав