Наиболее сложных заданий

4.1. Пример выполнения задания 2.4

Пусть требуется найти определитель:

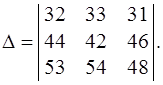
Поступим следующим образом: Сначала уменьшим элементы

матрицы, используя то свойство определителя, которое утверж-

дает, что он не меняется при вычитании из одной строки (или

столбца) другой строки (или столбца), умноженной на некото-

рое число. Для этого вычтем из второго столбца первый и из

третьего тоже первый. Получим

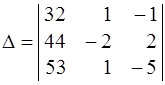. К 3-му столбцу прибавим 2-й: .

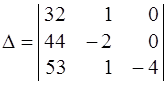Так как в 3-м столбце стоят 2 нуля, то вычисления упрощаются,

если разложить определитель по 3-му столбцу.

Получаем: 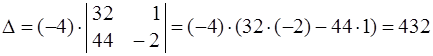. Проверить вычисления можно путем вычисления D на ЭВМ (см.раздел 3).

4.2. Пример выполнения задания 2.11

Пусть требуется решить матричное уравнение

.

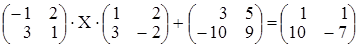Перенесём матрицу 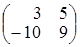в правую часть и вычтем из матрицы

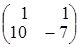. Получим 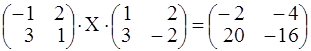. Умножим

полученное равенство слева на 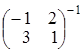и справа на .

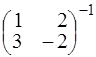Получим 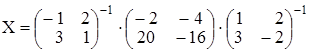. Далее, находим обрат-

ные матрицы ; .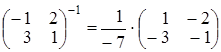

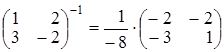Подставим в выражение для Х:

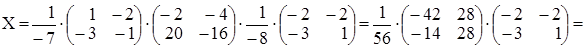
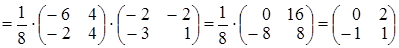. Проверим подстанов-

кой матрицы Х в исходное уравнение

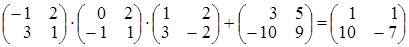. Вычисляем

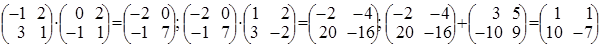
4.3. Пример выполнения задания 2.12

Пусть требуется решить уравнение .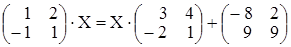

Обозначим элементы неизвестной матрицы 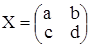и выполним

действия. В левой части равенства получим

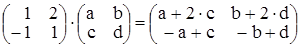. А в правой -

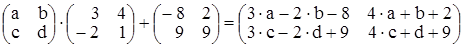. Приравнивая

соответствующие элементы матриц в левой и правой частях, полу-чим систему уравнений

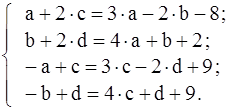
Переносим неизвестные в левую часть и приводим подобные члены:

.

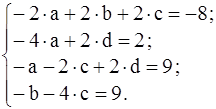Для решения системы можно обратиться к ЭВМ (см. раздел 3) или решить вручную. Выражаем d через a из 2-го уравнения и b через c из 4-го уравнения d = 1+2×a, b = - 9 - 4×c, и подставляем в 1-е и 3-е уравнения

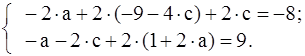
Сокращаем 1-е уравнение на 2 и приводим подобные члены

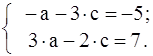
Прибавляя ко 2-му уравнению 1-е, умноженное на 3, получаем

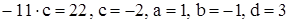. Получили искомую матрицу

.

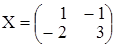Проверяем ответ подстановкой в матричное уравнение

.

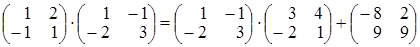Выполняя действия, получаем и в левой и в правой части одну

и ту же матрицу

.

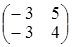4.4. Пример выполнения задания 2.13

Пусть нам дана система

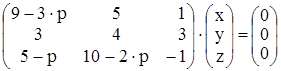. Так как система однородная, то для

того, чтобы она имела ненулевые решения, необходимо, чтобы её

определитель 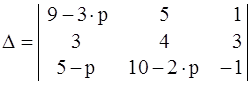был равен нулю.

Найдём такие значения р, при которых функция D(р) обращается в нуль. Найдём выражение для D(р), раскрывая определитель по пер-вой строке (на этом этапе можно обратиться к ЭВМ, см. раздел 3.3)

= .

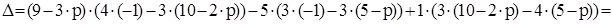
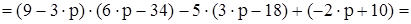
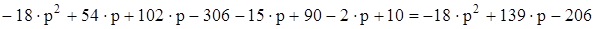Получаем квадратное уравнение: .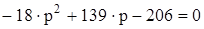

(Для его решения можно обратиться к ЭВМ). Находим его корни

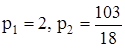. Далее находим для каждого р соответствующие ре-

шения системы (это можно также проделать на ЭВМ).

1. 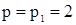. Получается система

.

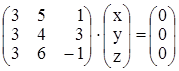Ищем общее решение этой системы (она должна быть неопределённой) методом Гаусса. При этом столбец свободных членов всегда будет нулевым и его можно не писать.

Приводим матрицу системы к стандартному ступенчатому виду

.

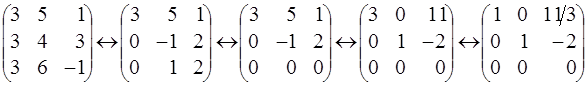Записываем систему, соответствующую последней матрице

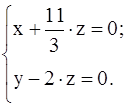
Получилось, что x, y – главные неизвестные; z – свободная неизвестная. Возьмём z = 1, тогда 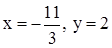. Нашли решение

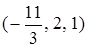, однако оно пока не удовлетворяет условию .

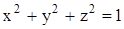Но так как наша система – однородная, то при умножении реше-ния на какое-либо число получается тоже одно из решений этой систе-мы. Тогда умножим полученное решение на такое число k, чтобы условие 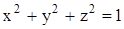было выполнено. Можно проверить подста-новкой, что можно взять 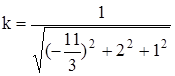. Для р = 2 получаем требуемое решение:

.

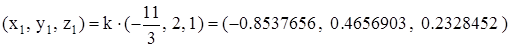2. 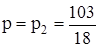. Получается система

.

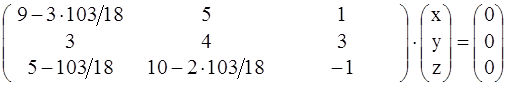Ясно, что как и в случае р = 2, третье уравнение будет следствием первых двух и его можно отбросить. Система получается неопределённая и можно взять х = 1. Найдём у и z

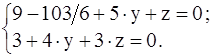
(Для решения можно обратиться к ЭВМ). Вычтем из 2-го уравнения 1-е, умноженное на 3

.

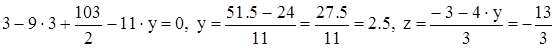Находим второе решение так же, как для р = 2

.

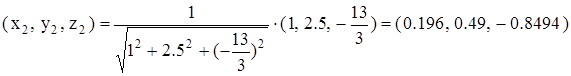Date: 2015-04-23; view: 428; Нарушение авторских прав