Обратите, пожалуйста, внимание на тот факт, что порядок полиномов в числителях этих дробей ровно на единицу меньше порядка полиномов в их знаменателях!

В результате сложения этих дробей получаем дробь: 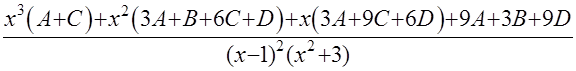, числитель которой должен в точности совпадать с числителем дроби исходной подынтегральной функции. Это позволяет сформировать систему теперь уже четырёх линейных уравнений для этих коэффициентов: .

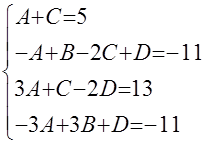Нетрудно показать, что решение этой системы: 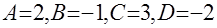и исходный интеграл равен сумме трёх интегралов: 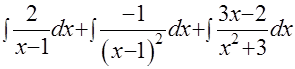. Первые два – табличные и их результат: 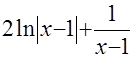. Решение последнего интеграла: . Итак, ответ:

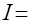
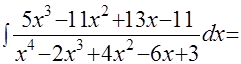
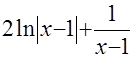
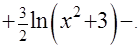
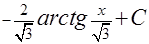
Обратите внимание на то, что громоздкий интеграл был сведён к комбинации табличных интегралов (решение последнего интеграла – см. Пример 3).

Пример 11. .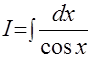

Рецепт. Покажем, что этот интеграл можно достаточно просто решить тем же методом «неопределённых коэффициентов». Для этого домножим числитель и знаменатель на 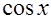. Подынтегральная функция примет вид 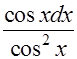. Опытный взгляд сразу увидит в числителе дифференциал функции 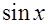. Отсюда возникает желание ввести замену: 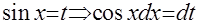. Далее подставляем эти выражения в подынтегральную функцию, и интеграл приобретает следующий вид: и готов к приложению к нему метода «неопределённых коэффициентов»: 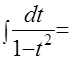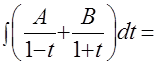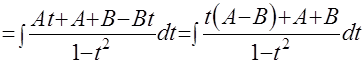. Знакомым уже способом получаем систему уравнений: 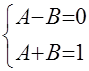. Из решения системы следует: 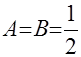и 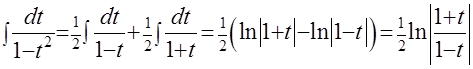. После обратной подстановки 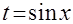получаем окончательный результат: .

Это очень полезный результат, поэтому есть смысл записать его в дополнительную таблицу неопределённых интегралов (см. табл.2).

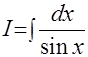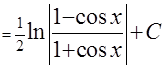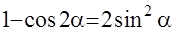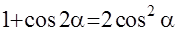Легко показать, что аналогичный интеграл = . С учётом формул и получаем ещё один вариант решения этого интеграла: 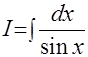= 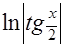+С. И этот результат рекомендуем внести в ту же дополнительную таблицу.

Date: 2015-06-05; view: 455; Нарушение авторских прав