
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

N.B.! Этот алгоритм, естественно, не единственный: можно было бы сделать замену или и др
|
|
ПРОВЕРКА
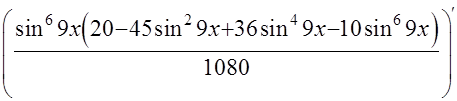 =
=
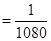
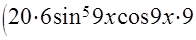 ─
─ 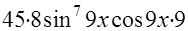 +
+

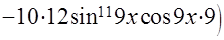 =
=
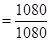
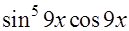
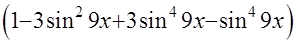 =
=
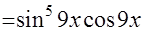
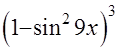 =
= 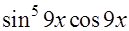
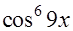 =
=
= 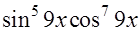 ─ правильность решения подтверждена.
─ правильность решения подтверждена.
Ответ: 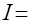
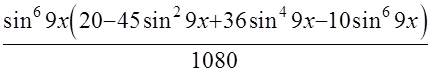 +С.
+С.
9. 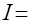
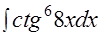 . Как было предложено в Примере 18, вводим замену
. Как было предложено в Примере 18, вводим замену 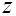 =
= 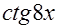 . Тогда
. Тогда 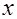 =
= 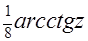
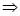
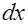 =
= 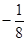
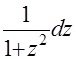 , а интеграл
, а интеграл 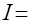
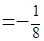
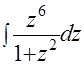 =
= 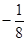
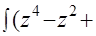
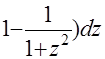 =
= 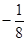
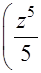
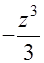 +
+ 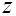 +
+ 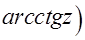 +
+
+С. Обратная подстановка даёт окончательное решение
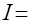
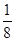
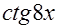
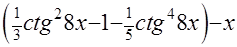 +С.
+С.
ПРОВЕРКА
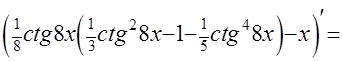
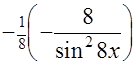
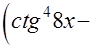
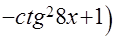
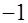 =
= 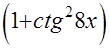
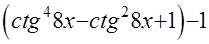 =
= 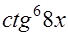 , что свидетельствует о правильности решения.
, что свидетельствует о правильности решения.
Ответ: 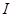 =
= 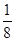
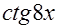
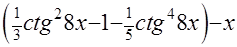 +С.
+С.
10. 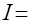
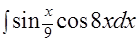 . Интеграл этого типа
. Интеграл этого типа 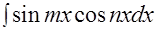 был рассмотренранее (см. выше стр.17). Согласно приведённым там рекомендациям воспользуемся формулой:
был рассмотренранее (см. выше стр.17). Согласно приведённым там рекомендациям воспользуемся формулой: 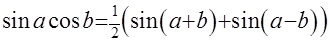 . Тогда
. Тогда 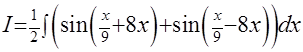 =
= 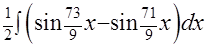 . Разбив этот интеграл на сумму двух «почти что табличных» интегралов и дважды воспользовавшись приёмом «замены аргумента» (см. Пример 1), получим решение
. Разбив этот интеграл на сумму двух «почти что табличных» интегралов и дважды воспользовавшись приёмом «замены аргумента» (см. Пример 1), получим решение 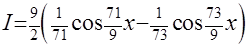 +С.
+С.
ПРОВЕРКА
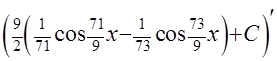 =
= 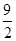
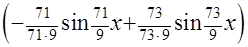 = =
= = 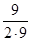
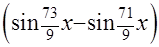 =
= 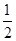
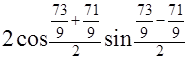 =
= 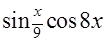 -желаемый результат!
-желаемый результат!
Ответ: 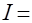
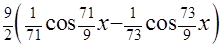 +С.
+С.
11. 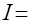
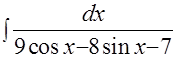 Этот интеграл по рекомендациям страницы 18 и 19 сводится к интегралу
Этот интеграл по рекомендациям страницы 18 и 19 сводится к интегралу 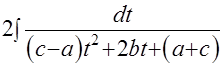 , для которого
, для которого 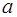 = 9,
= 9, 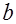 =- 8 и
=- 8 и 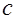 =- 7. Получаем интеграл
=- 7. Получаем интеграл 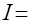
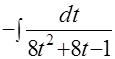 . Так как дискриминант знаменателя
. Так как дискриминант знаменателя 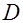 =32
=32 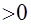 , то для решения данного интеграла подходит метод «неопределённых коэффициентов» (см. стр. 11 и 12). Для этого вычислим корни трёхчлена знаменателя:
, то для решения данного интеграла подходит метод «неопределённых коэффициентов» (см. стр. 11 и 12). Для этого вычислим корни трёхчлена знаменателя: 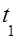 =
= 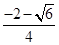 и
и 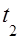 =
= 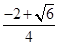 и перепишем наш интеграл в виде
и перепишем наш интеграл в виде 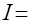
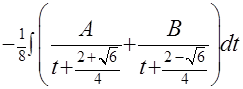 . После рутинных преобразований (см. Пример 20) получаем значения коэффициентов:
. После рутинных преобразований (см. Пример 20) получаем значения коэффициентов: 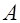 =
= 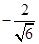 и
и 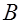 =
= 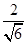 , а интеграл принимает свой промежуточный вид:
, а интеграл принимает свой промежуточный вид: 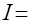
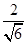
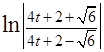 +С. После обратной подстановки окончательное решение
+С. После обратной подстановки окончательное решение 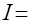
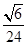
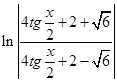 +С.
+С.
ПРОВЕРКА
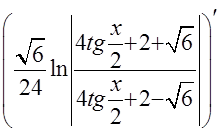 =
= 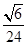
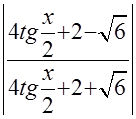
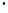
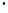
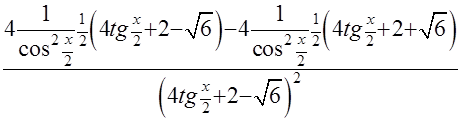 =
= 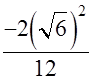
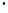
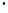
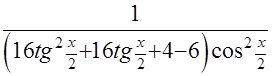 =
= 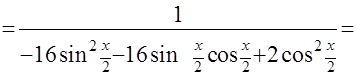
=  =
= 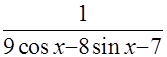 ─ очевидное свидетельство правильности взятия этого интеграла.
─ очевидное свидетельство правильности взятия этого интеграла.
Ответ: 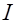 =
= 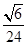
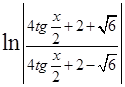 +С.
+С.
12. I= 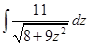 . Если из-под радикала знаменателя вынести
. Если из-под радикала знаменателя вынести 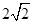 (см. стр. 19 и 20), то интеграл примет вид I=
(см. стр. 19 и 20), то интеграл примет вид I= 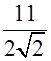
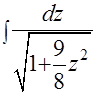 . Согласно рекомендациям на тех же страницах необходимо ввести замену
. Согласно рекомендациям на тех же страницах необходимо ввести замену 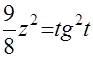
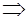
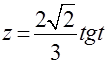
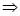
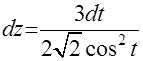
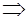
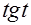 =
= 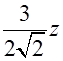 . После этого получаем интеграл I=
. После этого получаем интеграл I= 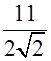
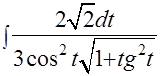 . Вспомнив, что
. Вспомнив, что 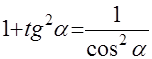 , получим I=
, получим I= 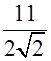
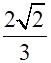 =
= 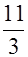
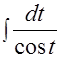 и, согласно дополнительной таблице интегралов, I=
и, согласно дополнительной таблице интегралов, I= 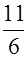
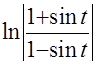 . Если вспомнить, что
. Если вспомнить, что 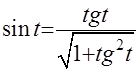
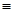
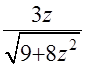 , то I=
, то I= 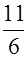
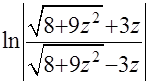 +С.
+С.
ПРОВЕРКА: 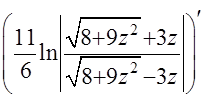 =
= 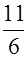
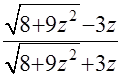
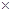
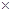
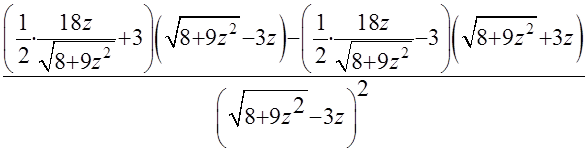 =
=
= 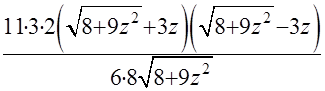 =
= 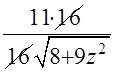 =
= 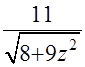 - мы убедились, что решение было верным.
- мы убедились, что решение было верным.
Ответ: 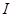 =
= 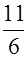
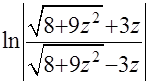 +С.
+С.
13. I= 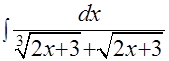 . Такой тип интеграла уже рассматривался на страницах 20 и 21. По рецепту, предложенному там, вводим новую переменную
. Такой тип интеграла уже рассматривался на страницах 20 и 21. По рецепту, предложенному там, вводим новую переменную 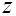 =
= 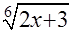 (6 - наименьшее общее кратное 2 и 3 –показателей радикалов знаменателя)
(6 - наименьшее общее кратное 2 и 3 –показателей радикалов знаменателя) 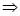
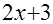 =
= 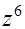
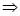
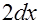 =
= 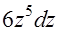
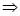
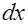 =
= 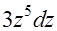 . Тогда интеграл примет вид: I=
. Тогда интеграл примет вид: I= 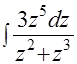 =
=  . Выделяем целую часть и остаток: I=
. Выделяем целую часть и остаток: I= 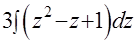
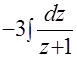 . А это уже табличные интегралы: I=
. А это уже табличные интегралы: I= 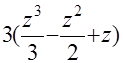
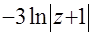 +С. После обратной подстановки и соответствующих преобразований решение интеграла получит следующий вид I=
+С. После обратной подстановки и соответствующих преобразований решение интеграла получит следующий вид I= 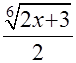
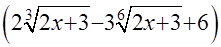
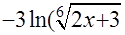
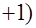 +С.
+С.
ПРОВЕРКА:
Сначала приведём решение к виду, более удобному для дифференцирования: 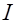 =
= 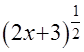
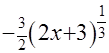 +
+ 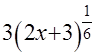 ─
─ 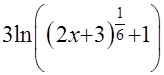 +С. Тогда
+С. Тогда 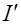 =
= 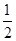
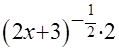

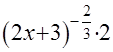 +
+ 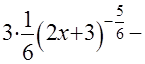
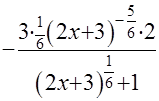 =
= 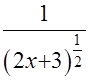
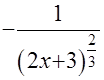 +
+ 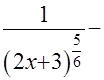
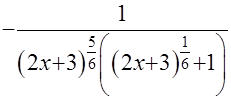
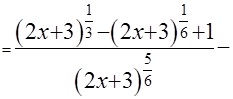
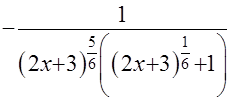 =
= 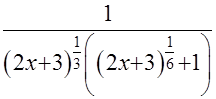 =
= 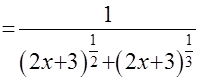 =
= 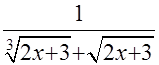 ─ полное совпадение с подынтегральной функцией.
─ полное совпадение с подынтегральной функцией.
Ответ: 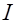 =
= 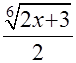
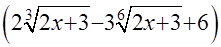
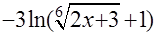 +С.
+С.
14. I= 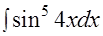 . При взгляде на подынтегральную функцию возникает естественное желание сделать замену аргумента
. При взгляде на подынтегральную функцию возникает естественное желание сделать замену аргумента 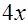 на какую-либо переменную, например,
на какую-либо переменную, например, 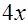 =
= 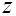
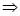
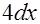 =
= 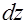
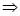
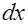 =
= 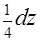 . Исходный интеграл преобразуется в
. Исходный интеграл преобразуется в 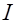 =
= 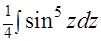 . Об интеграле этого типа речь шла на с. 23. Согласно предлагаемому на этой странице алгоритму подынтегральная функция сначала расщепляется на произведение
. Об интеграле этого типа речь шла на с. 23. Согласно предлагаемому на этой странице алгоритму подынтегральная функция сначала расщепляется на произведение 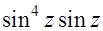 , затем преобразуется в
, затем преобразуется в 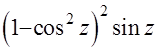 , откуда со всей очевидностью напрашивается замена:
, откуда со всей очевидностью напрашивается замена: 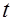 =
= 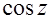
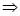
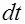 =
= 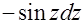
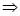
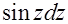 =
= 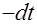 . Интеграл принимает вполне табличный вид
. Интеграл принимает вполне табличный вид 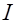 =
= 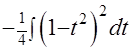 =
= 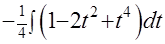 =
= 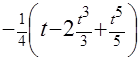 +С. После первой обратной замены
+С. После первой обратной замены 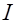 =
= 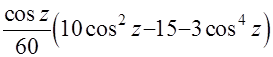 +С, а после второй и окончательной замены получаем
+С, а после второй и окончательной замены получаем 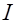 =
= 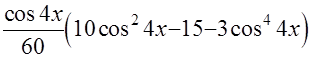 +С.
+С.
ПРОВЕРКА
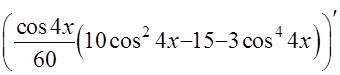 =
= 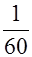
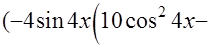
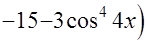 +
+ 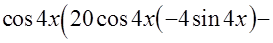
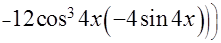 =
= 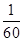
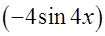
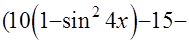
 =
= 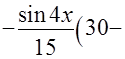
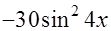
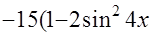 +
+ 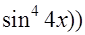 =
= 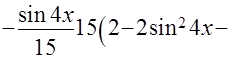
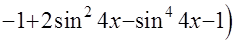 =
= 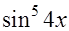 . Прекрасный результат!!!
. Прекрасный результат!!!
Ответ: 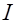 =
= 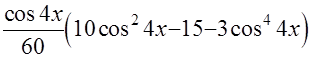 +С.
+С.
Библиографический список
1. Натансон И.П. Краткий курс высшей математики./ И.П.Натансон– СПб.: Лань, 2001.
2. Данко П.Е. Высшая математика в упражнениях и задачах/. П.Е.Данко и др.– М.:ООО Издательский дом ОНИКС 21век: ООО «Издательство «Мир и образование», 2003. Ч.1.
3. Соболь Б.В Практикум по высшей математике./ Б.В. Соболь, Н.Т. Мишняков., В.М. Поршкеян./ Ростов н/Д: Феникс, 2004.
4. Справочное пособие по математике./ И.И. Ляшко., А.К.Боярчук., Я.Г.Гай., Г.П. Головач. – М.: Едиториал УРСС, 2003. Т1.
5. Сборник заданий по высшей математике. Типовые расчёты. /Л.А. Кузнецов – СПб.: Лань, 2005
.
ПРИЛОЖЕНИЕ 1. Варианты заданий РГР.
Date: 2015-06-05; view: 657; Нарушение авторских прав