Матрицы влияния и их использование в расчетах балок

на примере балки, представленной на рис. 3.2, для которой нас интересуют эпюры изгибающих моментов от различных вариантов нагружения балки сосредоточенными силами в точках 1 2, 3, 4.

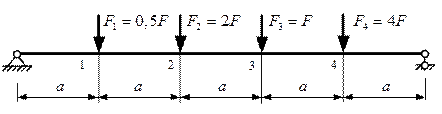
Рисунок 3.2

Матрица влияния изгибающих моментов [ L_М ]. Учитывая, что эпюра М
изменяется на участках между точками приложения сил линейно, сечения 1, 2, 3, 4 будут расчетными для получения эпюр М, и матрица влияния (3.3) будет квадратной.

Способ 1. Последовательно загружаем балку неподвижными единичными силами в точках 1, 2, 3, 4 и строим от их действия (рис. 3.3) единичные эпюры моментов. Из их ординат по столбцам формируем матрицу влияния (3.4). При этом для ординат эпюры М следует принять определенное правило знаков, которое должно согласовываться с правилом знаков для ординат линий влияния. Здесь это соответствует знаку «плюс» для растянутых волокон снизу (рис. 3.3).

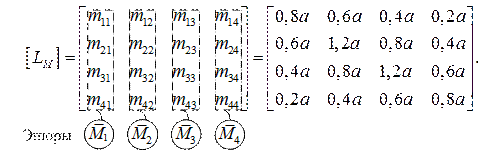
(3.4)

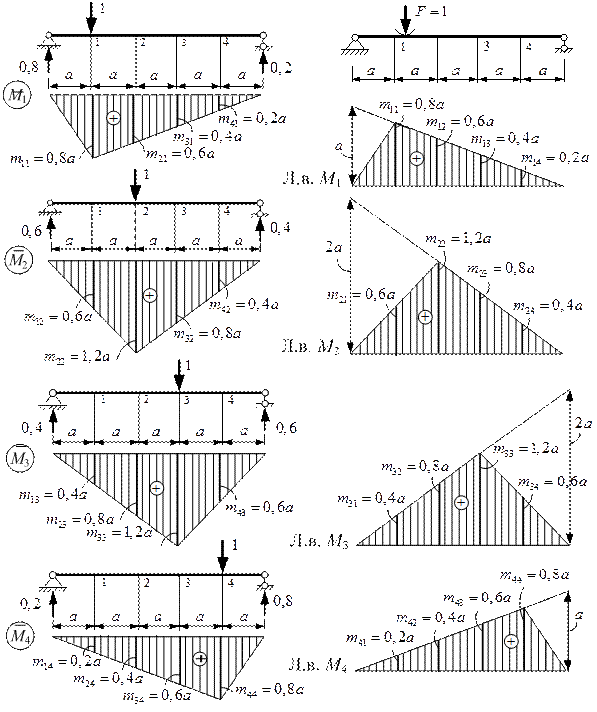
Рисунок 3.3 Рисунок 3.4

Способ 2. Строим линии влияния изгибающих моментов в расчетных сечениях 1, 2, 3, 4 от единичной силы, пробегающих всю балку (рис. 3.4). Из их
ординат по строкам формируем матрицу влияния [ L_М ]:

Образуем вектор внешних вертикальных сил:

.

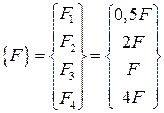Определим изгибающие моменты. Заменив в выражении (3.3) S на M, найдем изгибающие моменты в сечениях 1– 4:

;

.

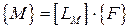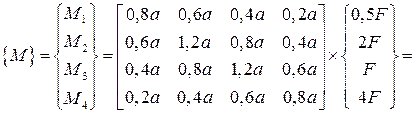
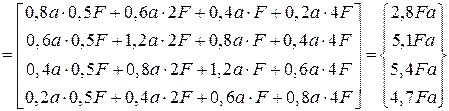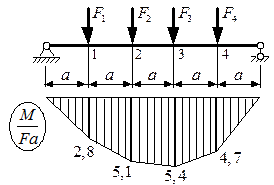Строим эпюру изгибающих моментов М от рассматриваемой нагрузки (рис. 3.5).

Заметим, что матричная форма расчета особенно удобна при исследовании
нескольких вариантов загружений одной и той же системы. Если значения внешних сил изменяется, новые значения внутренних сил легко найти, умножив матрицу влияния [ L_S ] на новый вектор .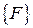

Date: 2015-05-22; view: 1677; Нарушение авторских прав