Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод Гаусса для решения систем линейных алгебраических уравнений
|
|
Рассмотренный подход требует большого объема трудоемких вычислений.
Широко для решения систем линейных алгебраических уравнений используется также метод Гаусса и его модификации. Метод основан на приведении матрицы системы к треугольному виду, что достигается последовательным
исключением неизвестных из уравнений системы.
Сначала с помощью первого уравнения исключается х1 из всех последующих уравнений системы. Затем с помощью второго уравнения исключается х2 из третьего и всех последующих уравнений. Этот процесс называется прямым ходом Гаусса, и продолжается он до тех пор, пока в левой части последнего уравнения не останется лишь одно слагаемое с неизвестным xn , то есть пока матрица системы [A] не будет приведена к треугольному виду.
Затем выполняется обратный ход Гаусса, который состоит в последовательном вычислении искомых неизвестных:
решая последнее уравнение, находим xn, затем из предпоследнего уравнения находим xn-1 и так до первого уравнения, из которого находим х1.
Рассмотрим применение метода Гаусса для системы трех уравнений:
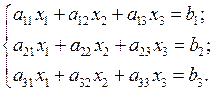(1.5)
Для исключения х1 из второго и третьего уравнений умножим первое уравнение последовательно на коэффициенты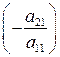 
и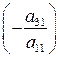 
(в общем случае на 
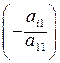) и сложим полученные уравнения соответственно со вторым и третьим уравнениями. В результате получим:
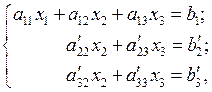(1.6)
где: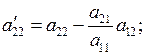 
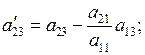
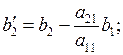
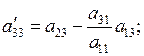
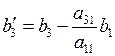
или в общем виде:
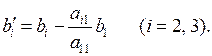
Теперь из третьего уравнения полученной системы (1.6) нужно исключить х2. Поступаем аналогично. Умножаем второе уравнение на коэффициент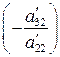 
и складываем полученное уравнение с третьим. Получим:
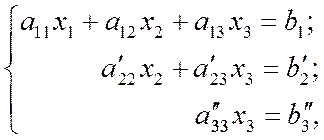
где: 
.
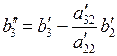Матрица системы уравнений стала треугольной, на этом заканчивается прямой ход Гаусса. Заметим, что здесь везде идет деление на коэффициенты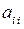 
, то есть на главные коэффициенты системы, поэтому они не должны быть равны нулю.
Обратный ход Гаусса начинается с решения последнего (третьего) уравнения: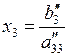 
,
после чего используя это значение, находим из второго уравнения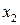 
:
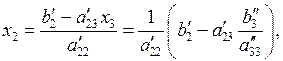
а затем, зная 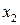и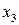 
, аналогично из первого уравнения находим 
.
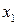Аналогично строится вычислительный алгоритм решений линейной
системы с произвольным числом уравнений. Заметим, что метод Гаусса – это достаточно удобный и широко применяемый метод решения систем линейных алгебраических уравнений.
При большом числе уравнений и значительном расхождении коэффициентов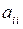 
в системе уравнений могут иметь место погрешности вычисления неизвестных, которые могут быть весьма значительными.
Date: 2015-05-22; view: 512; Нарушение авторских прав