Итерационные методы решения систем линейных алгебраических уравнений

Далее рассмотрим методы, которые позволяют уточнять решения, полученные прямыми методами (методом Гаусса).

Эти методы называются итерационными.

Пусть мы нашли решение системы линейных алгебраических уравнений (1.1)

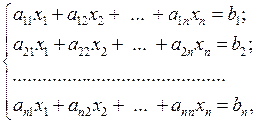
например, методом Гаусса, которое дает следующие значения неизвестных:

, , … .

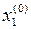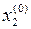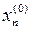Подставляя эти значения в исходную систему уравнений, получим свободные члены, соответствующие данному решению:

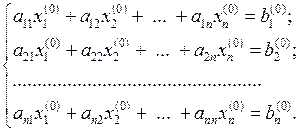(1.7)

Вычисляем теперь невязку (расхождение) свободных членов:

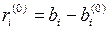. (1.8)

Подставляя невязку в систему уравнений (1.1) вместо свободных членов, получим систему уравнений

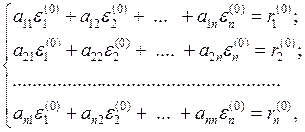(1.9)

в которой в качестве неизвестных будем иметь погрешности вычисления неиз-

вестных: 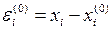. (1.10)

Решая систему уравнений (1.9), найдем эти погрешности, после чего
вносим поправки в величины неизвестных:

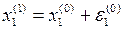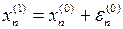; ;……… . (1.11)

Первая итерация закончена.

Теперь выполняем вторую итерацию с полученными неизвестными
по аналогичной процедуре (1.7) – (1.11). Процесс продолжается до тех пор,
пока все очередные значения погрешностей не станут достаточно малыми.

Может быть задана величина допускаемой погрешности 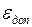, имея
которую на каждом этапе необходимо делать оценку погрешностей вычисления неизвестных

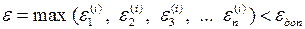. (1.12)

Это критерий по абсолютной погрешности.

Если условие (1.12) выполняется, то это значит, что процесс завершен.
Такой процесс является сходящимся.

7. Общая система уравнений равновесия стержневых систем и её применение к расчету статически определимых ферм.