Метод Ритца для решения задачи устойчивости стержня

Заметим также, что для определения констант многочленов часто используются условия, связанные с физическим поведением объектов (в том числе, как уже указывалось, с тем, что системы деформируются, затрачивая минимум энергии).

В качестве примера рассмотрим задачу, решение которой известно из
сопротивления материалов – задачи об устойчивости стержня (рис. 5.6). Крити-

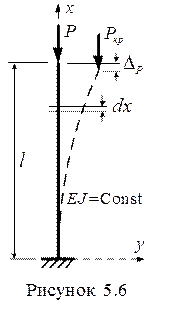ческая сила по Эйлеру для такого стержня равна

.

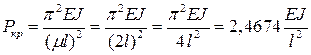Допустим, мы этого не знаем, и не знаем, по какой кривой происходит потеря устойчивости. Примем для формы потери устойчивости многочлен

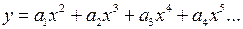. (5.8)

Для определения констант 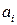используем метод
Ритца, который предложил искать форму потери устойчивости исходя из условия минимума энергии системы:

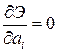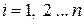, . (5.9)

Полная энергия стержня при потере устойчивости здесь будет состоять из трех слагаемых:

– из начальной энергии системы до потери устойчивости (до критического состояния) 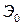– эта энергия относительно параметров интерполяции является константой;

– из энергии изгиба стержня при потере устойчивости;

– из потенциальной энергии силы Р, равной работе этой силы с обратным знаком – ;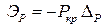

– из энергии сжатия стержня, которая здесь мала и мы ею пренебрежем.

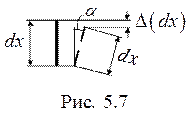
Для определения величины перемещения силы Р по вертикали (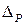) рассмотрим вначале бесконечно малый элемент стержня (рис. 5.7), и определим разницу между его первоначальной длиной и проекцией повернутого в результате изгиба элемента на первоначальное направление:

.

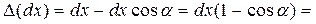
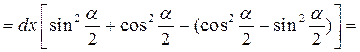
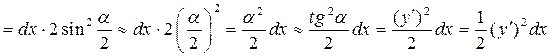Вертикальное перемещения силы Р определим, выполнив интегрирование полученного выражения по всей длине стержня

,

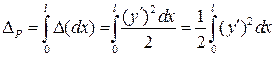после чего изменение потенциала внешней нагрузки получим в виде:

.

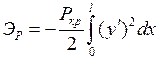Энергия деформации стержня определяется выражением:

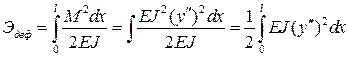, где .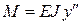

Получаем полную потенциальную энергию стержня в виде:

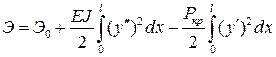. (5.10)

Для простоты дальнейших расчетов возьмем два слагаемых аппроксимации (5.8): ;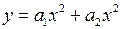

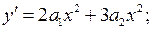
Подставляем эти зависимости в выражение для полной потенциальной энергии:

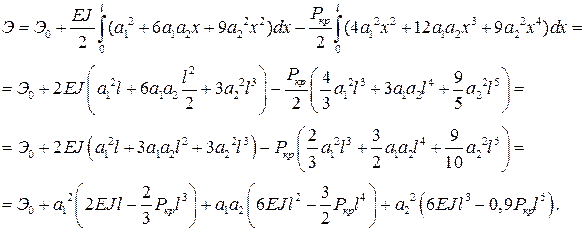
Применяем к этому выражению процедуру метода Ритца (5.9):

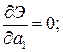
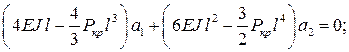
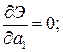
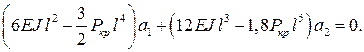
Получаем однородную систему уравнений, решение которой будет отлично от нуля только в том случае, если определитель системы будет равен нулю:

.

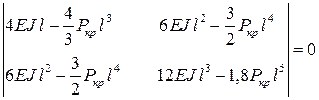Раскрывая этот определитель, получаем квадратное уравнение

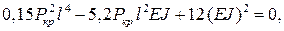
решение которого дает для рассматриваемой сжатой стойки значение критической силы:

Сравнивая этот результат с решением Эйлера, получаем расхождение в 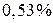. Величина расхождения невелика. Таким образом, уже при двух слагаемых многочлена (5.8) мы получили приемлемое решение.

При трех слагаемых получим более точное значение, однако будем иметь кубическое уравнение, которое так просто не решить. Если взять многочлен четвертого порядка, уравнение будет ещё более сложным.

Получаемые уравнения являются нелинейными и решаются часто очень
не просто.

Численное интегрирование. Основные понятия и виды.

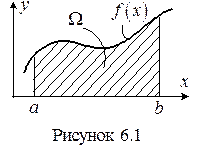Из математики известно, что определенный интеграл 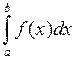представляет собой по физическому смыслу площадь фигуры,

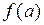ограниченной осью x, функцией и ординатами и 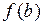– площадь Ω (рис. 6.1).

С другой стороны, известно, что

,

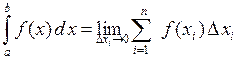и если 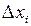принимать конечной величиной, то получим формулу для приближенного вычисления интеграла методом прямоугольников:

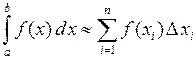, (6.1)

где: 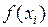– одна из ординат функции в пределах участка Δ х_i; участки Δ х_i часто удобно принимать одинаковой величины (Δ х_i = Δ х).

В зависимости от положения ординаты 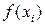различают три варианта
численного вычисления интегралов:

1) если точки x_i на участках Δ х берутся слева, то будем иметь сумму
левых прямоугольников (рис. 6.2, а);

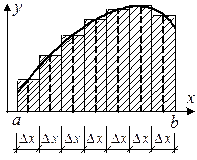
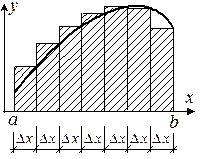а) б) в)

Рисунок 6.2

2) если на участках 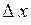берутся правые ординаты, то будем иметь сумму правых прямоугольников (рис. 6.2, б);

3) если возьмем средние значения функции на участках Δ х, то получим сумму прямоугольников, базирующихся на средних ординатах (такой подход часто называют методом средних) (рис. 6.2, в).

Вероятно, последний вариант будет точнее, чем два предыдущих, однако для его применения необходимо дополнительно вычислять средние ординаты на участках.

Для численного вычисления интегралов используются и другие подходы, приводящие к еще более точным результатам.

Ниже рассмотрим некоторые из них.

Date: 2015-05-22; view: 2347; Нарушение авторских прав