Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Замечание
|
|
Если система линейных алгебраических уравнений однородная, то есть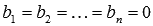 
, то она имеет лишь тривиальное решение 
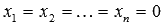(при 
). Действительно, при нулевых свободных членах все определители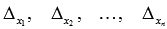 
будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы 
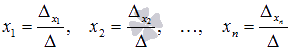дадут .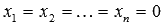
Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.
1. Вычисляем определитель основной матрицы системы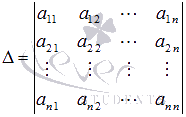 
и убеждаемся, что он отличен от нуля.
2. Находим определители
которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.
3. Вычисляем искомые неизвестные переменные x1, x2, …, xn по формулам .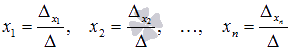
4. Выполняем проверку результатов, подставляя x1, x2, …, xn в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.
Примеры решения систем линейных алгебраических уравнений методом Крамера.
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера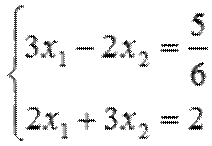 
.
Решение.
Основная матрица системы имеет вид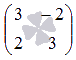 
. Вычислим ее определитель по формуле 
:
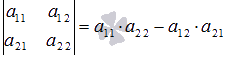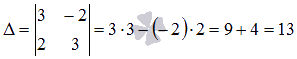
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определител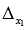и 
и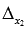 
. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель 
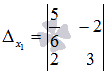. Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем 
.
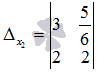Вычисляем эти определители:
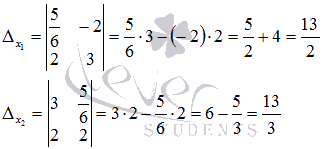
Находим неизвестные переменные x1 и x2 по формулам 
:
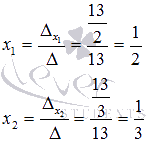
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
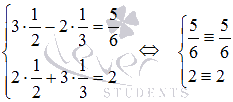
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
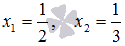Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
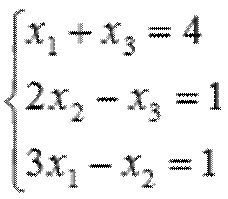
Найдите решение системы линейных уравнений методом Крамера .
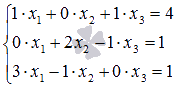
Решение.
Перепишем систему в виде , чтобы стало видно основную матрицу систмы .
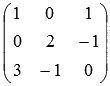
Найдем ее определитель по формуле
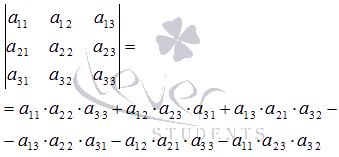
Имеем
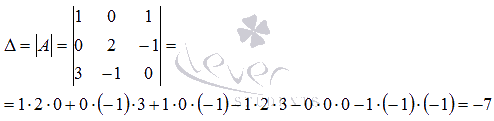
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители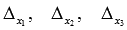 
:
Таким образом,
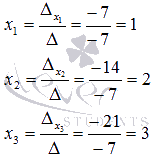
Ответ:
.
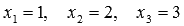Date: 2015-05-22; view: 596; Нарушение авторских прав