Линейная, квадратичная и другие виды интерполяции

В зависимости от максимальной степени задаваемого многочлена различают линейную, квадратичную, кубическую и другие интерполяции.

1. Линейная интерполяция – заданные точки соединяют прямыми линиями, получая для ряда точек ломаную линию. Уравнение каждого из отрезков определяется уравнением прямой, проходящей через две точки

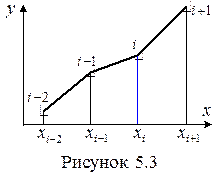
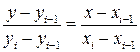, (5.5)

которое можно преобразовать в уравнение прямой в классическом виде

,

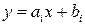где: .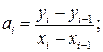

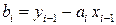Зависимость справедлива при .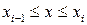

2. Квадратичная (параболическая) интерполяция – задается на отрезке трех точек (например, от 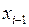до 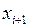) в виде:

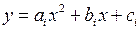(5.6)

и содержит три константы, для определения которых необходимо составить три уравнения. Для записи этих уравнений используются известные ординаты в указанных точках:

– при ;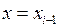

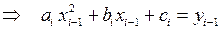– при ;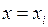

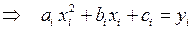– при .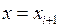

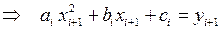Решая представленную систему трех уравнений, определяем значения констант аппроксимации .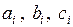

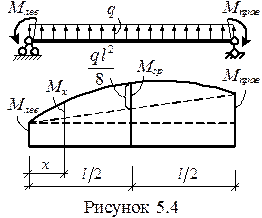
С помощью такой интерполяции можно, например, строить эпюру изгибающих моментов 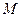на участке действия распределенной нагрузки, когда известны значения изгибающих моментов по краям и в середине участка (рис. 4). Тем более, что нам известно, что изгибающий момент на прямолинейном участке стержневой системы действительно изменяется по параболической зависимости, и поэтому результат будет соответствовать точному.

Задаем аппроксимирующую функцию в виде: .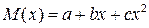

В качестве условий для нахождения констант а, b и c используем известные значения этой функции в крайних и средней точках:

а) пр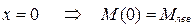и или ;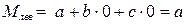

б) при 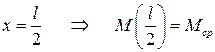или ,

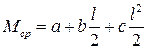где 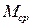определяется зависимостью (рис. 5.4):

;

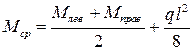в) при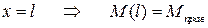

или .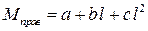

Решаем два последних уравнения:

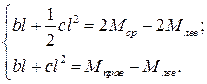
Отнимая из второго уравнения первое, получим выражение, из которого выразим с:

.

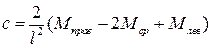Из второго уравнения теперь найдем b:

.

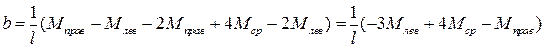В результате получаем:

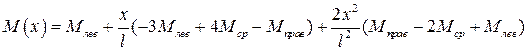. (5.7)

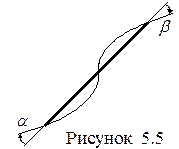3. Кубическая интерполяция. Широкое распространение для интерполяции получило использование кубических сплайн-функций – специально построенных многочленов третьей степени, представляющих собой математическую модель изгиба упругого стержня при заданных условиях поворотов его концов (углов α и β на рис. 5.5). Форма изгиба стержня (функция интерполяции) при этом определяется путем минимизации потенциальной энергии стержня, деформирующегося в заданных условиях.

4. В общем случае для n точек – на участке 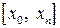можно задать полином n -ой степени:

,

подставив в который ординаты для всех известных точек, получим систему n уравнений для определения всех .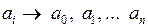

Date: 2015-05-22; view: 2761; Нарушение авторских прав