Ангармонічний осцилятор

Застосовуючи стаціонарну теорію збурень, знайти у першому та другому наближеннях рівні енергії та хвильові функції частинки в полі

, (1)

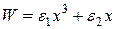
(ангармонічний осцилятор).

Відомо (див., наприклад, []), що розв’язання незбуреної задачі при (гармонічний осцилятор) дає невироджені власні значення оператора 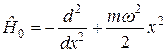, які дорівнюють:

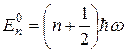. (2)

Тому для знаходження власних значень і власних функцій оператора 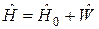застосуємо теорію збурень при відсутності виродження. У другому порядку теорії збурень маємо:

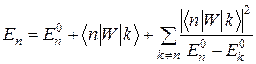(3)

і

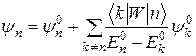, (4)

де 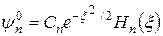, 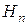- поліном Ерміта, , .

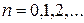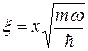Задача зводиться до обчислення матричних елементів

,

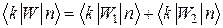де 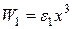і 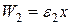. Використовуючи властивості ортогональності поліномів Ерміта, можна обчислити наступні матричні елементи координати :

,

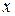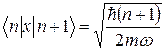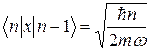, (5)

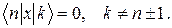
Результати (5) можна переписати у компактнішому вигляді:

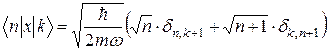. (6)

Обчислимо матричні елементи 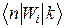, використовуючи (6) та правило множення матриць:

.

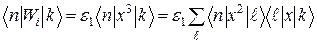У свою чергу

.

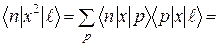
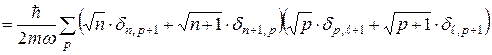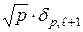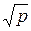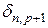Очевидно, що у добутках виду можна замінити на і на 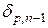. В силу цього

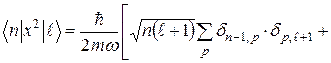
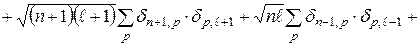
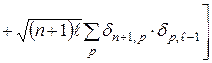
і, наприклад, перший доданок буде рівний

;

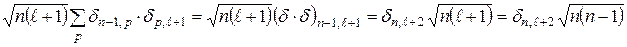позаяк 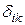є одиничною матрицею, то .

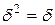Виконавши подібну операцію з усіма членами, одержимо:

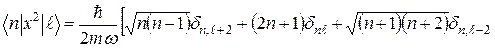. (7)

Підставивши цей вираз у 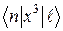і виконавши аналогічні обчислення, можемо написати

.

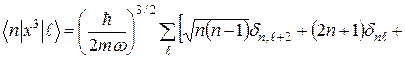
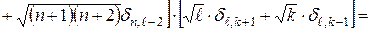
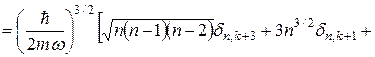
Таким чином, 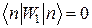і 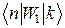для заданого відмінний від нуля лише у чотирьох випадках: при 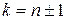і 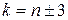. Значить, цей член дає поправку у формулі (3) лише у другому порядку, а у формулі (4) – у першому, і ми можемо обмежитися лише ними. Враховуючи, що знаменники формул (3) і (4) при 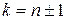дорівнюють 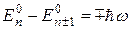, а при 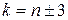- 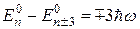, можна записати

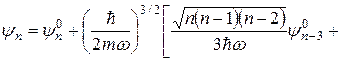(8)

.

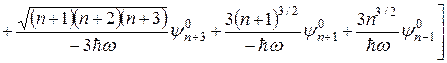При обчисленні енергії необхідно врахувати поряд із поправкою другого порядку від 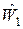також і поправку першого порядку від 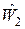, тобто обчислити 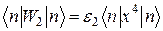. Аналогічно одержимо

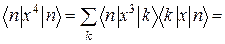
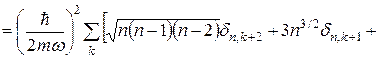
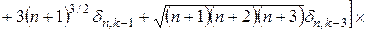(9)

.

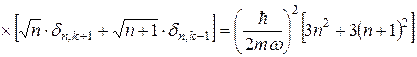Зазначимо, що відмінні від нуля результати одержимо лише при множенн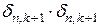і і 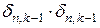. Інші члени дорівнюють нулю, наприклад, .

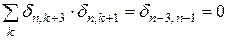В результаті маємо

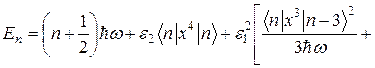
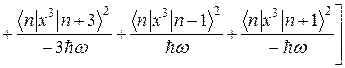
і після підстановки обчислених матричних елементів одержимо остаточний результат:

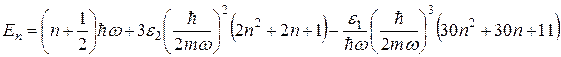. (10)

Date: 2015-05-19; view: 758; Нарушение авторских прав