Сферично симетрична прямокутна потенціальна яма

Розглянемо взаємодію між частинками, яка описується потенціалом, абсолютна величина якого достатньо швидко (швидше, ніж 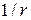) спадає при 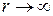. У багатьох випадках можна вважати, що на деякій відстані взаємодією можна взагалі знехтувати, поклавш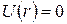и при 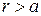. Такі потенціали називають короткодіючими, а параметр - радіусом їх дії.

Прикладом швидко затухаючого потенціалу притягання є потенціал Вудса-Саксона

, (1)

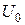де , і 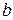- деякі додатні параметри (рис.3.11). Такий потенціал широко використовується у ядерній фізиці для описання взаємодії нейтронів з атомними ядрами. Параметр визначає розміри області локалізації взаємодії, а параметр 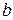- розміри тої області, де відбувається найбільш швидка зміна потенціалу. При 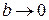потенціал (1) переходить у потенціал сферично симетричної прямокутної потенціальної ями радіуса (див. рис.3.11).

Знайдемо енергії і хвильові функції стаціонарних станів для руху частинки у полі сферично симетричної прямокутної потенціальної ями з потенціальною енергією:

(2)

Нехай орбітальний момент частинки 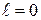. Оскільки потенціал (2) сферично симетричний, хвильову функцію 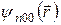можна представити у вигляді

, (3)

де “радіальна” функція 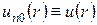задовольняє рівняння Шредінґера

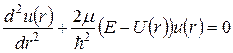. (4)

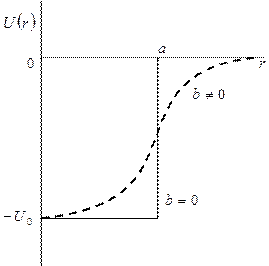
Рис. 3.11. Потенціали Вудса-Саксона та сферично симетричної

прямокутної потенціальної ями

Розв’язки рівняння (4) повинні задовольняти початковій умові

. (5)

Шукаємо енергію в інтервалі 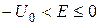. У просторовій області (І) маємо

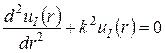, (6)

де .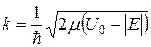

Розв’язок рівняння (6) має вигляд

.

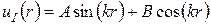Із граничної умови (5) одержимо , тому

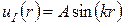. (7)

У просторовій області (ІІ) маємо

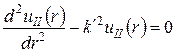, (8)

де .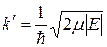

Розв’язок рівняння (8) має вигляд

.

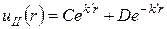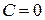Із умови квадратичної інтегрованості функції одержимо , тому

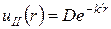. (9)

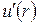Використаємо тепер умови неперервності функції та її похідної в точці :

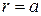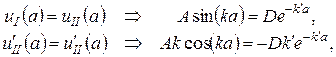
звідки одержимо трансцендентне рівняння

. (10)

Рівнянню (10) відповідає графік на рис. 3.12.

Рис. 3.12

Date: 2015-05-19; view: 519; Нарушение авторских прав