Потенціального бар’єру. Тунельний ефект та надбар’єрне відбивання

Розглянемо рух частинки в полі, де її потенціальна енергія 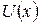має форму прямокутного бар’єра (рис. 3.4):

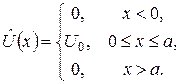(1)

Потрібно визначити коефіцієнти відбивання і прозорості вказаного бар’єра.

Власні функції оператора Гамільтона

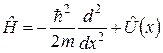, (2)

тобто розв’язки стаціонарного рівняння Шредінґера

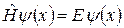(3)

розіб’ємо на три гілки:

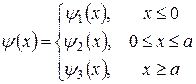(4)

Стаціонарні рівняння Шредінґера для 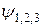мають вигляд:

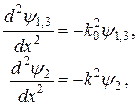(5)

де .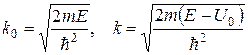

Загальні розв’язки рівняння (5) визначаються виразами

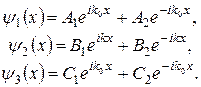(6)

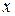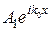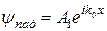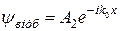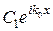Сформулюємо тепер постановку задачі про відбивання та проходження частинки через потенціальний бар’єр, у випадку, коли до взаємодії з бар’єром вона рухається у додатному напрямку осі . У цьому випадку вираз описує падаючі частинки, а вираз - відбиті. Отже, ; ; . У третій області не може бути частинок, які б рухалися у зворотному напрямку, тому слід покласти . Вираз описує частинки, що пройшли потенціальний бар’єр, тобто .

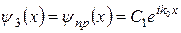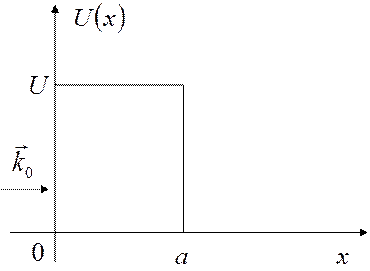Рис. 3.4. Прямокутний потенціальний бар’єр

Введемо тепер експериментально вимірювані технічні коефіцієнти – відбивання:

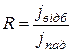(7)

і прозорості бар’єра:

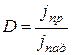, (8)

де 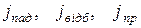- величини густин потоків відповідно падаючих частинок, відбитих частинок і частинок, що пройшли бар’єр. Використовуючи формулу, що виражає густину потоку через хвильову функцію

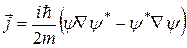, (9)

одержимо

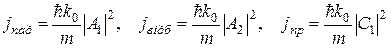. (10)

Підставивши (10) у (7) і (8), одержимо:

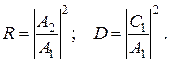(11)

Використаємо тепер умови неперервності хвильової функції 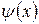та її похідної 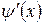в точках 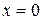і :

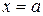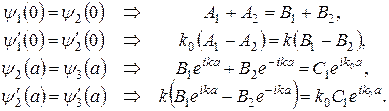(12)

Система (12) – це система 4-х лінійних рівнянь для 5-и невідомих 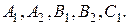Але, оскільки для визначення коефіцієнтів відбивання 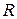і прозорості 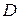нам потрібно знати лише відношення 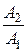і 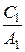, то поділивши рівняння системи (12) на 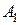, одержимо 4-и рівняння для 4-х невідомих

:

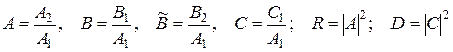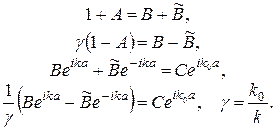(13)

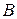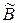Виразимо і через 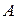з перших двох рівнянь системи (13):

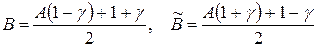. (14)

Підставивши (14) в останні два рівняння в (13), одержимо рівняння для визначення :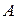

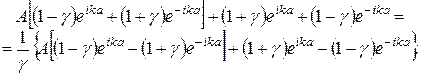(15)

Із (15) маємо:

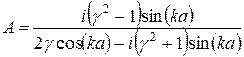. (16)

Тепер знаходимо :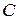

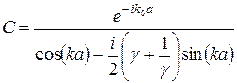. (17)

Щоб обчислити квадрати модулів цих виразів, зручно перш за все розглянути випадок, коли 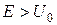, і, отже, величина 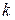є дійсною. Тоді

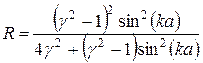, (18)

, (19)

Легко бачити, що 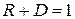, що випливає із збереження числа частинок: .

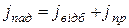Оскільки

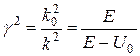, (20)

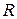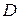а , то замість (18) і (19) одержимо остаточні вирази для і при :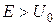

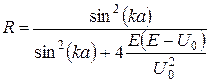, (21)

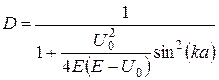. (22)

Відмітимо, що у випадку класичної частинки при 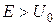має бути 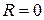(а, отже, 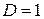) – тобто всі частинки “пролітають” над бар’єром. Для квантової частинки, якщо 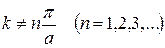, коефіцієнт відбивання 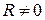. Це явище має назву надбар’єрного відбивання. Лише при 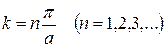реалізуються значення (своєрідна “резонансна прозорість” бар’єру, див. рис. 3.5).

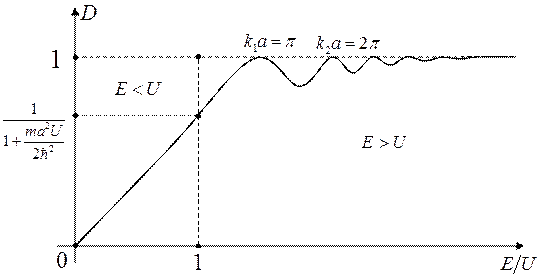
Рис. 3.5. Залежність коефіцієнта прозорості D від енергії Е

для прямокутного бар’єра висотою U і шириною a

Перейдемо тепер до більш цікавого випадку 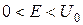. У цьому випадку

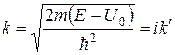, (23)

де 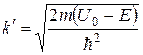- дійсна величина.

Тоді 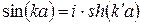і, отже, аналітичне продовження виразів (21) і (22) під бар’єр приводить до виразів

, (24)

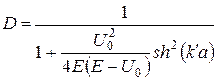. (25)

Для класичної частинки при 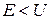коефіцієнт прозорості 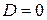(а, відповідно, 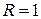), оскільки кінетична енергія 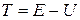не може бути від’ємною. Отже, для квантової частинки при 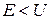коефіцієнт прозорості 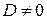, що принципово відрізняється від класичного випадку – це специфічно квантовий ефект, що отримав назву “тунельного ефекту”.

Розглянемо граничні випадки, що випливають із виразів (24) і (25):

а) при 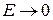маємо: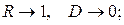

б) при 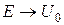, розкривши невизначенність типу 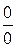, одержимо

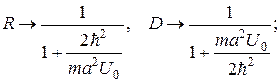
в) при 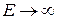маємо: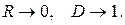

На рисунку 3.5 зображено графік залежності коефіцієнта прозорості 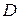від енергії 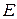. Зазначимо, що спектр резонансних значень енергії (при ), коли бар’єр стає повністю прозорим, має таку ж структуру (лише зсунуті на величину 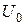), як і для енергій стаціонарних станів частинки у безмежно глибокій потенціальній ямі (див. задачу 2):

.

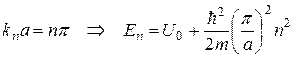У цьому випадку на ширині бар’єру відкладається ціле число півхвиль де Бройля: . У випадку бар’єра значної ширини і висоти, коли 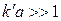, 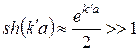і тому вираз для можна представити у вигляді:

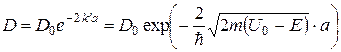. (26)

Вираз (26) може бути узагальнений і на випадок бар’єра довільної форми (див. рис. 3.6); результат має вигляд:

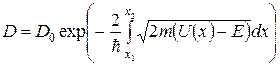, (27)

де точки повороту 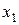та 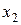знаходяться із умови 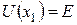і .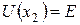

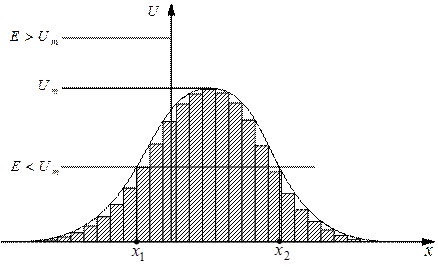Рис. 3.6. Потенціальний бар’єр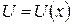

Date: 2015-05-19; view: 1319; Нарушение авторских прав