Розпад важких ядер

Стала розпаду 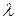визначає відносну кількість ядер, що розпалися за одиницю часу:

. (1)

Тому ця величина пропорціональна коефіцієнту прозорості 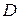: , що дає можливість застосувати формулу (27) задачі №4 і одержати наступне співвідношення:

, (2)

де 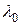- деяка стала, що має розмірність таку ж, як і 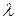, тобто 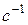; 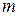- маса -частинки.

Ще в 1911 році Г. Гайтлер і Дж. Нетол встановили таку емпіричну залежність (див. (1))

(3)

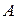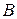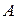де і - константи, що залежать від характеристик ядра, а - швидкість -частинки. Як видно з рис. 3.9, із приведеного графіка легко визначити параметри і .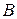

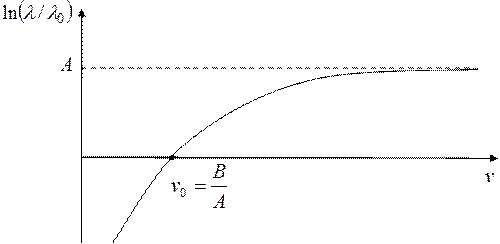
Рис. 3.9.

Завдання. Одержати формулу (3), розглядаючи -розпад, як тунелювання -частинок через бар’єр, утворений ядерним та кулонівським потенціалами; визначити залежність параметрів 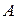і 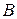від характеристик ядра.

Потенціальну енергію -частинок представимо як суму двох потенціалів – ядерного та кулонівського :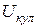

,

де

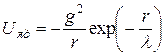, (4)

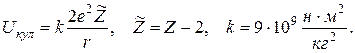(5)

Оскільки вид потенціальної енергії -частинки всередині ядра, тобто при 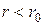( 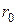- “радіус” ядра), є несуттєвим, то для обчислень можемо використати такий спрощений вид потенціалу (рис.3.10):

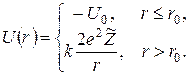(6)

Рис. 3.10.

Використовуючи (6), із (2) одержимо[1]:

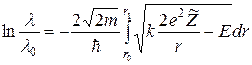, (7)

де точка повороту визначається умовою:

. (8)

Для обчислення інтегралу в (7) перейдемо до нової змінної:

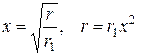. (9)

Підставивши (9) у (7), з урахуванням (8) одержимо:

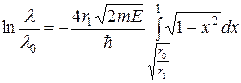. (10)

Використовуючи вираз для первісної

, (11)

і підставляючи (11) у вираз (10), одержимо:

. (12)

Природно припустити, що ; зберігаючи при цьому у степеневому розкладі лише члени першого порядку за 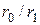, матимемо

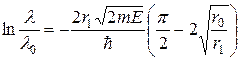. (13)

Оскільки поза ядром для нерелятивістської -частинки 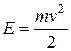, то одержимо таку кінцеву формулу

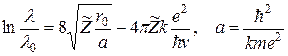. (14)

Порівнявши (14) з (3), визначимо параметри 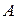і :

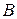. (15)

Date: 2015-05-19; view: 503; Нарушение авторских прав