Скінченої глибини

Розглянемо рух частинки маси 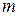в полі з потенціальною енергією 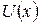(див. рис. 3.1):

(1)

Таке ідеалізоване поле часто використовується для описання руху частинок в реальних полях з великим градієнтом в окремих малих областях простору (наприклад, рух електронів в металевій пластинці малих розмірів).

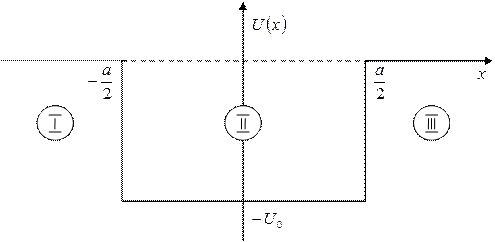
Рис. 3.1. Одновимірна прямокутна потенціальна яма

Оскільки гамільтоніан частинки в полі (1)

(2)

є парним, тобто 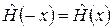, то він комутує з оператором парності : .

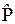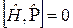Нагадаємо, що за визначенням оператора :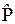

. (3)

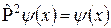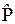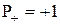Тому стаціонарні стани можна класифікувати за певним значенням парності. Позаяк із (3) випливає, що , то власними значеннями оператора є: і . Отже, набір стаціонарних станів розбивається на два класи: а) парні стани 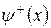, для яких 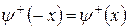і б) непарні стани 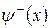, для яких .

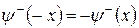Знайдемо стаціонарні розв’язки рівняння Шредінґера

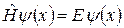(4)

в інтервалі енергій .

Позначимо:

(5)

і

. (6)

Тоді рівняння Шредінґера в областях І, ІІ і ІІІ (див. рис. 3.1) запишеться у вигляді:

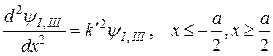(7)

і

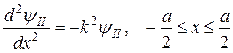. (8)

Загальні розв’язки рівнянь (7), (8):

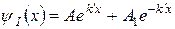, (9)

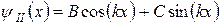, (10)

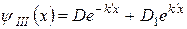. (11)

Із умови квадратичної інтегрованості хвильової функції 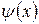одержимо:

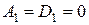. (12)

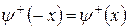Далі, для парних станів : ; а для непарних станів : .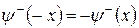

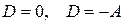Отже, для стаціонарних парних станів одержимо:

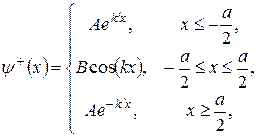(13)

a для непарних стаціонарних станів –

(14)

Визначимо тепер значення енергії 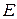стаціонарних станів (13) і (14) (через яку виражаються параметри 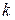і ). Розглянемо спочатку парні стани (13). Використаємо умови неперервності функції 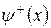та її похідної в точці :

,

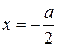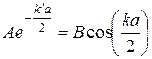(15)

.

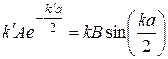Система (15) має нетривіальні розв’язки тоді і тільки тоді, коли параметри і 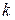задовольняють рівняння:

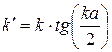. (16)

Розглянемо тепер непарні стани. З умови неперервності функції 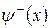та її похідної в точці :

,

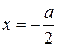(17)

.

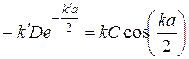Система (17) має нетривіальні розв’язки тоді і тільки тоді, коли параметри і 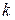зв’язані рівнянням:

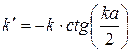. (18)

Із (5) і (6) випливає, що в обох випадках – парних і непарних станів - параметри і 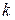зв’язані наступним рівнянням:

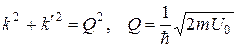. (19)

На координатній площині 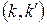графіком рівняння (19) є коло, радіус 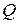якого пропорціональний кореню квадратному із глибини ями 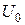. Точки 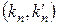, які визначають енергії стаціонарних станів

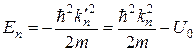(20)

розташовані в першій чверті 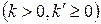на перетині вказаного кола з графіками рівнянь: (16) – для парних станів і (18) – для непарних станів. Тому доцільно використати графічний метод для дослідження розв’язків трансцендентних рівнянь (16) і (19) - для парних станів та (18) і (19) - для непарних станів (див. рис. 3.2).

Висновки з представленого графічного аналізу:

1) в кожній смужці шириною 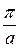(по осі абсцис) знаходиться рівно один стаціонарний стан, причому парні стани знаходяться в непарних номерах 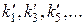(їм відповідають енергії ), а непарні стани - в парних номерах 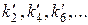(їм відповідають енергії 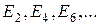). Завжди існує хоча б один перший стан – за будь-яких значень 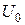та ;

2) непарні стани існують лише за умови, що 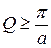, тобто ; при невиконанні цієї умови для частинки існує лише один дискретний стан, який є першим;

3) кількість всіх стаціонарних станів (як парних, так і непарних) при заданих параметрах ями 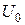та визначається умовою:

,

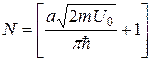де символ 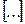позначає цілу частину числа. Доведення цього твердження пропонується читачеві.

Рис. 3.2. Графічний аналіз рівнянь (16), (18)

Після визначення дискретних значень енергії 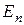стаціонарних станів, в хвильових функціях цих станів (13) і (14) залишається по одному невизначеному коефіцієнту (в силу однорідності систем (15) і (17)). Цей останній коефіцієнт виражається з умови нормування:

.

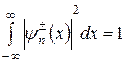При 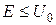та стаціонарних станів не існує. Читачеві пропонується обґрунтувати це твердження самостійно.

Date: 2015-05-19; view: 496; Нарушение авторских прав