Вправи на закріплення розуміння формалізму КМ

2.1. Комутаційні співвідношення

Вправа 1. Визначити комутатор .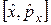

Розв’язання. Для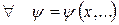

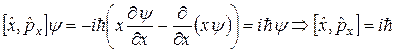. (2.1)

Відповідь: .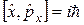

Вправа 2. Виписати всі можливі комутатори в сукупності операторів .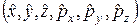

Відповідь:

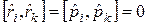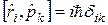; . (2.2)

Тут 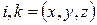- позначення індексів операторів проекцій радіус-вектора 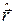та імпульсу .

Вправа 3. Визначити комутатор операторів 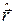та кінетичної енергії .

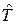Розв’язання. Використовуючи вираз (1.12), запишемо

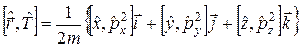. (2.3)

Визначимо комутатори у фігурній дужці, використовуючи (2.1):

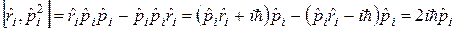, . (2.4)

Підставивши (2.4) у вираз (2.3), одержимо

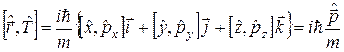. (2.5)

Відповідь: .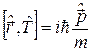

Вправа 4. Встановити комутаційні співвідношення між операторами проекцій моменту імпульсу .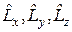

Розв’язання. Обчислимо як приклад комутатор (інші два комутатори обчислюються аналогічно)

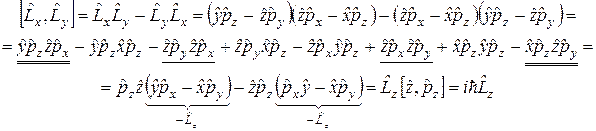
Відповідь:

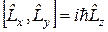, (2.6)

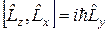, (2.7)

. (2.8)

Вправа 5. Довести, що кожний з операторів 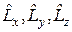комутує з 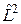, тобто

.

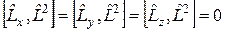2.2. Імовірності результатів вимірювань,

середні значення та дисперсії фізичних величин

Вправа 6. Показати, що з умови нормування хвильової функції

(2.9)

та умови ортонормування власних функцій ермітового оператора

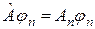, (2.10)

а саме

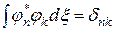(2.11)

випливає, що набір 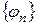є повним, тобто при розкладанні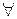 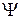у ряд

(2.12)

виконується співвідношення

. (2.13)

При цьому визначає імовірність того, що при вимірюванні величини 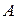над системою, що перебуває в стані 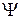, ми одержимо значення 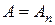. Цю імовірність позначатимемо

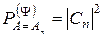. (2.14)

Вправа 7. Використовуючи (2.11) і (2.12), довести, що

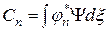. (2.15)

Співвідношення (2.15) дозволяє представити вираз (2.14) у вигляді:

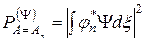. (2.16)

Вправа 8. Показати, що середнє значення величини 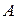у стані 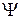, визначається формулою

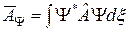. (2.17)

Вказівка. Для доведення (2.17) підставити розклад (2.12) в (2.17) і, використовуючи (2.10), (2.11) і (2.14), одержати співвідношення

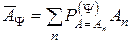, (2.18)

що є стандартним визначенням середнього значення (надалі індекс 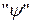в середньому значенні не виписуємо).

Вправа 9. Визначити середнє значення потенціальної енергії електрона в основному стані атома водню

, (2.19)

де 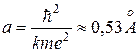- радіус Бора.

Розв’язання. За означенням середнього значення

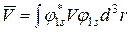. (2.20)

Оскільки 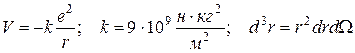, то

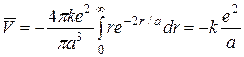. (2.21)

Відповідь: .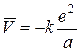

Вправа 10. Визначити середнє значення кінетичної енергії електрона в основному стані атома водню.

Розв’язання. Перш за все запишемо оператор 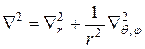, де 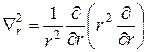. Тоді

,

звідки одержимо:

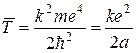. (2.22)

Із (2.21) і (2.22) видно, що 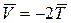- аналог відомої теореми віріала в класичній механіці.

Відповідь: .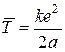

Вправа 11. Визначити дисперсію координати 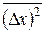в основному стані лінійного гармонічного осцилятора:

.

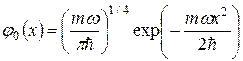Розв’язання. Маємо:

, оскільки .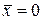

Тому

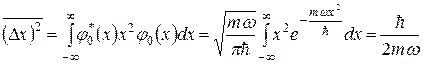. (2.23)

Відповідь: .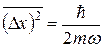

Вправа 12. Визначити дисперсію імпульсу 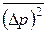в основному стані лінійного гармонічного осцилятора.

Розв’язання. Маємо:

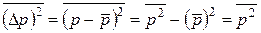, оскільки .

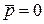Тому

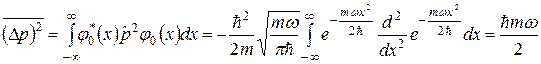. (2.24)

Відповідь: .

Висновки із вправ (2.11) і (2.12):

1) У розглянутому випадку співвідношення Гайзенберга мінімізується. Дійсно, з (2.23) та (2.24) слідує, що

. (2.25)

Такі стани в КМ називаються когерентними.

2) Середні значення потенціальної 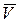та кінетичної лінійного гармонічного осцилятора дорівнюють одне одному і рівні половині енергії основного стану 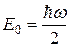. Дійсно, 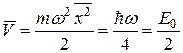, а також .

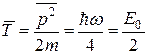Date: 2015-05-19; view: 478; Нарушение авторских прав