
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантова частинка в полі -подібної потенціальної ями
|
|
Розглянемо наступну модельну задачу: маємо одновимірну прямокутну потенціальну яму з одним єдиним енергетичним рівнем (див. рис. 3.3). Необхідно визначити умову прямування ширини цієї ями до нуля, а глибини – до нескінченості, при якій енергія рівня залишається незмінною.
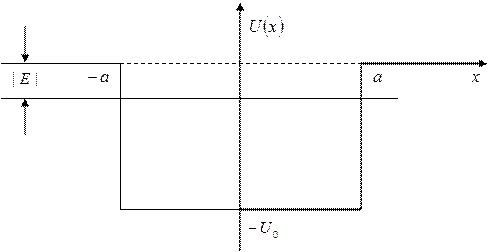 |
Рис. 3.3. Одновимірна прямокутна потенціальна яма з одним рівнем
Із результатів задачі №2 випливає, що хвильова функція частинки, яка знаходиться на єдиному енергетичному рівні, що існує у ямі, як і хвильова функція будь-якого основного стану, не може мати вузлів, тобто має бути парною (відносно середини ями). Використовуючи формули (13) задачі №2, для хвильової функції частинки всередині ями 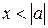 маємо:
маємо:
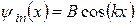 , (1)
, (1)
де
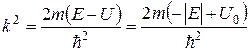 ,
,
а зовні ями справа  :
:
 , (2)
, (2)
де
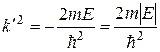 .
.
Прирівнюючи логарифмічні похідні функцій (1) і (2) на правій границі ями (при 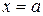 ), одержимо:
), одержимо:
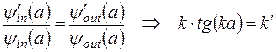 . (3)
. (3)
Спрямуємо тепер, як вимагається в умові задачі, 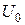 до нескінченності і
до нескінченності і  - до нуля. При цьому
- до нуля. При цьому 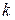 буде прямувати до
буде прямувати до 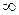 . Але за умовою задачі
. Але за умовою задачі 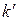 має залишатися сталим, тому, як випливає з (3),
має залишатися сталим, тому, як випливає з (3), 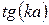 має прямувати до нуля. Це дозволяє нам замінити значення тангенса значенням його аргументу, тобто
має прямувати до нуля. Це дозволяє нам замінити значення тангенса значенням його аргументу, тобто
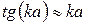 . У результаті із (3) знайдемо:
. У результаті із (3) знайдемо:
 , (4)
, (4)
або
 . (5)
. (5)
Таким чином, при прямуванні  до нуля, а
до нуля, а 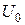 - до нескінченності їх добуток залишається сталим:
- до нескінченності їх добуток залишається сталим:
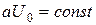 . (6)
. (6)
Якщо переписати вираз (6) у вигляді
 , (7)
, (7)
то відповідь на поставлене в умові задачі питання можна сформулювати так: для того, щоб енергія рівня залишається незмінною, необхідно прямувати ширину ями до нуля, а глибину – до нескінченості так, щоб “площа перерізу” ями залишалася сталою.
Знайдемо граничні умови для функцій 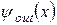 за межами ями. Позначимо розв’язок зліва від ями
за межами ями. Позначимо розв’язок зліва від ями  , а справа -
, а справа - 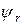 (зазначимо, що поза ямою може існувати довільний додатковий потенціал). Розв’язок всередині ями рівний
(зазначимо, що поза ямою може існувати довільний додатковий потенціал). Розв’язок всередині ями рівний
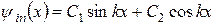 . (8)
. (8)
Гранична умова зліва від ями (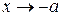 ) має вигляд:
) має вигляд:
 (9)
(9)
Розв’язавши систему рівнянь (9) відносно 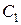 і
і  , одержимо:
, одержимо:
 (10)
(10)
Гранична умова справа від ями (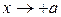 ) має вигляд:
) має вигляд:
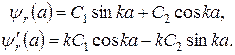 (11)
(11)
Підставляючи в (11) знайдені раніше значення 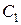 і
і  (10), виразимо
(10), виразимо 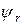 і
і 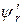 через
через  і
і 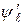 :
:
 (12)
(12)
Перейдемо тепер до границі
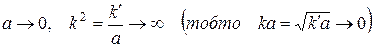 ,
,
одержимо:
 ,
,
або, замінюючи згідно (4) 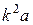 на
на 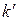 :
:
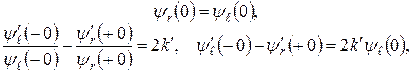 (13)
(13)
де 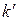 - єдина стала, яка характеризує яму і безпосередньо зв’язана з величиною енергії рівня у ній:
- єдина стала, яка характеризує яму і безпосередньо зв’язана з величиною енергії рівня у ній:
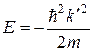 .
.
Умову (13) можна сформулювати у вигляді потенціалу, що має вид 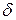 -функції
-функції
 .
.
Дійсно, інтегруючи рівняння Шредінґера

( - довільний, але гладкий додатковий потенціал) по малому інтервалу
- довільний, але гладкий додатковий потенціал) по малому інтервалу 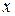 в околі
в околі 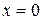 , одержимо:
, одержимо:
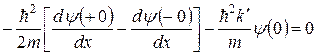 ,
,
або
 ,
,
що співпадає з умовою (13).
Зазначимо, що потенціал, який зображає прямокутну яму, при прямуванні  із забезпеченням при цьому умови (7) (рівність “площі перерізу” ями)
із забезпеченням при цьому умови (7) (рівність “площі перерізу” ями)
 ,
,
прямує до 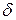 -функції з коефіцієнтом
-функції з коефіцієнтом  , що рівний за модулем площі прямокутника на рис. 3.3.
, що рівний за модулем площі прямокутника на рис. 3.3.
Date: 2015-05-19; view: 686; Нарушение авторских прав