Итоги решения задачи об атоме водорода

Задача об атоме водорода выше решена в общем виде. На основе полученных результатов можно детально описать стационарные состояния электрона. Они определяются тройкой квантовых чисел n, l и m.

Квантовые числа позволяют рассчитать для каждого состояния значения трех физических величин, имеющих одновременно определенные значения. Это энергия, момент импульса и его проекция:

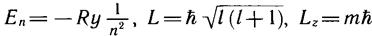
Согласно формуле (11.6) n = n_r + l + 1, т. е. n=>l+1. Поэтому при заданном главном квантовом числе орбитальное квантовое число пробегает п разных значений от 0 до n-1. При фиксированных n и l может быть 21+1 состояний, отличающихся значениями магнитного квантового числа. Нам потребуется в дальнейшем знать количество состояний с одним и тем же п, но различными I к т. Оно определяется суммированием состояний с различными т по всем значениям l:

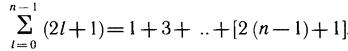
Используя формулу суммы арифметической прогрессии, имеем

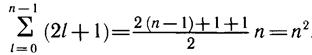
Такова кратность вырождения уровней энергии электрона в атоме водорода, так как все эти состояния имеют одну и ту же энергию.

Имеется и все необходимое, чтобы записать полную функцию состояния атома водорода — радиальный и угловой ее сомножители известны и определяются формулами (11.8) и (10.8). Итак,

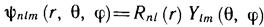. (11.21)

Согласно выражениям (10.10) и (11.10) функции состояния

ψ_nlm (r, θ, φ) нормированы условием

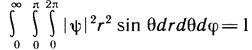
11.4. Водородоподобные системы.

Date: 2015-05-19; view: 498; Нарушение авторских прав