Движение частицы в центрально-симметричном поле

Центрально-симметричным называется силовое поле с потенциальной энергией, зависящей только от расстояния до некоторого центра Центр удобно взять в качестве начала координат: U = U(r)

Сила, действующая на частицу в таком поле, направлена по радиусу. Поэтому при движении классической частицы сохраняется не только полная механическая энергия, но и момент импульса. В силу принципа соответствия следует ожидать появления тех же

интегралов движения и в квантовой механике.

Для изучения стационарных состояний нужно решить уравнение Шредингера (8.4) для движения в центральном силовом поле. Симметрия поля подсказывает, что следует воспользоваться сферическими координатами:

Нψ(r, θ, φ) = Y _lm (θ, φ),

где гамильтониан имеет вид

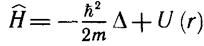(10.4)

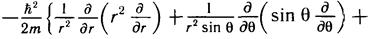
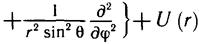
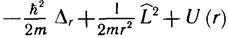
обозначен оператор:

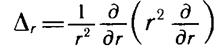
Если внимательно рассмотреть формулы (10.3), (10.5) и (10.14), то нетрудно установить, что операторы H, L² и L_z коммутируют друг с другом. Отсюда следует, что существуют

стационарные состояния, в которых одновременно заданы энергия, момент импульса и его проекция на некоторую ось, принятую за ось Oz.

Уравнение (10.14) допускает разделение переменных. Ищем волновую функцию в виде произведения радиального и углового множителей:

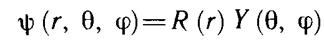
После подстановки получаем уравнение

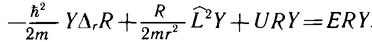
Умножим его на -2mr² и разделим на RY. Уравнение примет вид

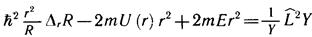
Правая и левая части этого равенства есть функции разных независимых переменных, поэтому они должны быть равны одной и той же постоянной величине. Обозначим ее через λ. Теперь исходное уравнение Шредингера распадется на два уравнения

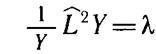
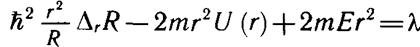
Первое из них есть уравнение для собственных функций и собственных значений оператора квадрата момента импульса. Его решение нам известно. Используя данные предыдущего пункта, заключаем, что угловая часть волновой функции ψ(r, θ, φ) выражается одной из сферических функций Y _lm (θ, φ), a λ = ћ²l (l+l).

Учитывая значения λ, запишем второе уравнение в виде

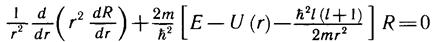
Это уравнение называется радиальным. Для его предварительного анализа сделаем подстановку:

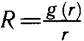
(10.17)

Новая искомая радиальная функция g (r) удовлетворяет уравнению

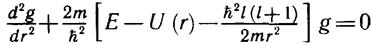(10.18)

Оно по форме совпадает с одномерным уравнением Шредингера для движения частицы в поле с эффективным потенциалом:

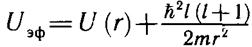(10.19)

Дальнейшее решение задачи о движении частицы в центрально- симметричном поле требует знания вида потенциала U (г).

Соберем воедино все найденные сведения по вопросу о движении частицы в центральном поле:

1) Возможны стационарные состояния с определенными значениями энергии, момента импульса и его проекции на ось Oz.

2) Указанные состояния различаются квантовыми числами l и m, определяющими момент импульса частицы и его проекцию.

3) Энергия стационарного состояния зависит от конкретного вида центрального поля и должна быть определена вместе с радиальным множителем в формуле (10.15) в процессе решения уравнения (10.16) или (10.18).

Полезно заметить, что эти выводы справедливы для любого постоянного тилового поля с центральной симметрией. Далее их используем для решения конкретной задачи об атоме водорода, задаваясь для радиального уравнения кулоновским потенциалом:

.

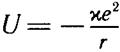Date: 2015-05-19; view: 853; Нарушение авторских прав