II. 1. Постановка задачи об атоме водорода

Энергия ионизации атома водорода примерно 13,6 эВ, что намного меньше энергии покоя

электрона (0,51 МэВ). Следовательно, задача об атоме водорода может решиться в рамках нерелятивистской квантовой механики — выполняется закон сохранения числа частиц, а также можно применять нерелятивистское уравнение Шредингера. Если пренебречь весьма малыми магнитными взаимодействиями, о которых речь пойдет дальше, то можно считать, что электрон находится в поле кулоновской силы электростатического притяжения к ядру. Потенциальная энергия электрона выражается классической формулой

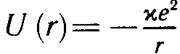, (11.1)

где r — расстояние электрона до ядра, а

.

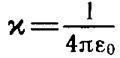постоянная величина. Поле является центрально-симметричным, и мы можем воспользоваться всеми результатами предыдущего параграфа.

При решении задачи об атоме водорода интерес представляет движение электрона по отношению к ядру; ядро считается неподвижным. Это оправдано, так как масса ядра почти в 2000 раз больше массы электрона. Однако для сопоставления теоретически найденных уровней энергии с экспериментальными, измеряемыми с точностью до 8 и более значащих цифр, необходимо учесть, что ядро тоже движется вокруг центра масс атома. Как в классической механике, так и в квантовой учет движения ядра в формулах

для динамических параметров системы прост; нужно лишь заменить в уравнениях движения массу электрона на приведенную массу.

(о классической задаче двух тел см. ч. I, § 15). Поэтому уравнение Шредингера приведет к формуле энергии электрона, где вместо m

стоит μ. Что касается функции состояния, то можно считать, что она характеризует движение электрона относительно ядра в системе, связанной с движущимся в пространстве ядром (подробнее о квантовой задаче двух частиц см. § 14).

Ниже полагаем, что ядро находится в начале координат. Массу электрона — приведенную или обыкновенную — обозначаем через μ.

Угловая часть волновой функции электрона уже известна: это сферическая функция

Y_lm(θ,φ). Для нахождения радиальной части нужно решить радиальное уравнение (10.16) или (10.18) с новским потенциалом. В данном случае эффективный потенциал

имеет вид

,

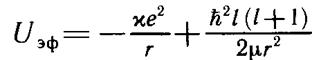Общий ход кривой (U_эф дан на рисунке 5.1. При r ->0 (U_эф ведет себя как 1/r², на больших расстояниях функция Uэф(r) приближается к нулю как 1/r со стороны отрицательных значений. Для нас наиболее важна область потенциальной ямы. Здесь при отрицательных

энергиях движение частицы происходит в ограниченной области пространства и возможны связанные состояния с дискретными значениями энергии.

Date: 2015-05-19; view: 903; Нарушение авторских прав