Свойства оператора момента импульса и его проекций

Одной из важнейших величин, характеризующих вращательное

движение макроскопических тел, является момент импульса. Еще

большее значение он приобретает в квантовой механике, особенно

в физике атомов и молекул, где часто момент импульса отдельных

частиц или систем имеет определенные значения наряду с энергией.

108Чтобы детально исследовать строение атомов, необходимо преж-

прежде познакомиться с квантовыми особенностями момента импульса.

Напомним вид оператора этой физической величины:

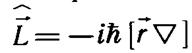
L=—ih[rV]. (10.1)

Запишем операторы проекций момента импульса на оси декарто-

декартовых координат:

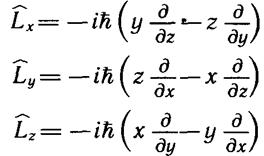
Можно показать, что операторы L^_x, L^_y и L^_z удовлетворяют перестановочным соотношениям:

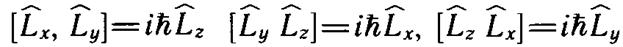
. (10.2)

Так как они не коммутируют друг с другом, то не существует состояний с тремя определенными проекциями момента импульса (за исключением случая L_x = L_y = L_z = 0).

Оператор квадрата момента импульса:

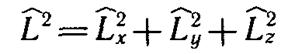
коммутирует с операторами проекций L_x, L_y и L_z. Это означает, что возможны состояния с определенным модулем момента импульса (с определенным значением величины L²) и какой-нибудь из его проекций.

При изучении движения частицы в центральном поле целесообразно использовать сферические координаты r, θ и φ. Перейдем в формулах для проекций момента к переменным r, θ и φ. Известно, что

x = r sin θ cos φ, y = r sin θsin φ, z = r cos θ

В сферических координатах получаем (см. задачи 1, 2, 11 к главе IV)

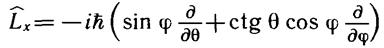
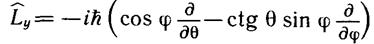
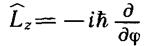
(10.3)

Поскольку ось Oz выбрана в качестве полярной оси, равноправие трех декартовых осей координат Ох, Оу и Oz при переходе к сферическим координатам теряется: теперь некоторое направление в пространстве выделено, и удобно рассматривать состояния с

определенными значениями L ^ ² и L ^ _z.

10.2. Собственные значения и собственные функции операторов L^² и L^_z.

Коммутирующие операторы L ^ ² и L ^ _z имеют общую систему

109собственных функций. Для того чтобы найти эти функции, нужно

решить уравнение

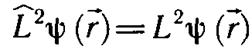. (10.4)

В сферических координатах

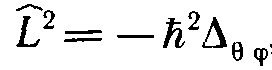, (10.5)

где

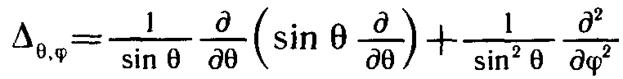
Поэтому уравнение (10.4) сводится к дифференциальному уравнению

в частных производных:

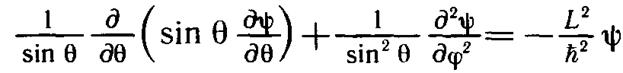
хорошо известному в математике (см. любой курс методов матема-

математической физики, раздел «Уравнение Лапласа в сферических коор-

координатах»). Оно имеет однозначные, непрерывные и всюду ограни-

ограниченные решения при условии

L² = ћ²l(l+1), l = 0, 1,2,..., (10.7)

которым определяются собственные значения оператора квадрата

момента импульса.

Искомые решения уравнения (10.4) называются сферическими

функциями. Сферическая функция индексов l и m обозначается

символом Y_lm. Она имеет вид

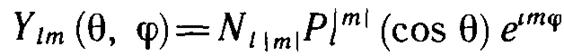(10.8)

где P_l^|m| (cos θ) — присоединенный полином Лежандра от аргумента cos θ.

Приведем выражение для полиномов Лежандра x = cos θ:

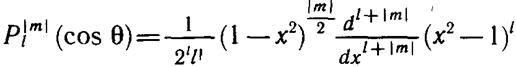
Если сферические функции нормированы условием

то нормировочный множитель в формуле (10.8) таков:

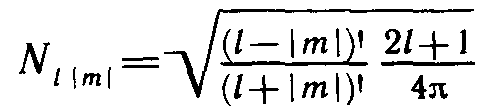
(Произведение sin θdθdφ есть элементарный телесный угол dΩ. Следовательно, в нтеграле (10.10) производится интегрирование по всем возможным направлениям в пределах полного телесного угла, равного 4л.)

ПОФункции с неодинаковыми индексами I или т ортогональны друг другу:

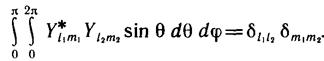
л 2л

\ \ YtmJ,!m2sine de dy = bUhbmim,

о о

Выпишем несколько сферических функций:

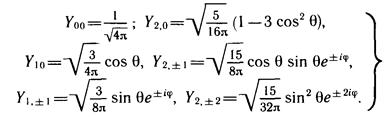
(10.11)

Квантовое число I определяет модуль момента импульса. Состояния с небольшими значениями I часто обозначаются буквами латинского алфавита.

Говорят, например, что частица находится в р-состоянии, или, другими словами, что ее момент импульса равен 1. Это означает, что l =1 и L = ћ√2.

Состояния с заданным моментом импульса вырождены по квантовому числу m. Физический смысл второго квантового числа раскрывается при решении задачи о, собственных функциях и собственных значениях оператора проекции момента импульса L_z.

Уравнение

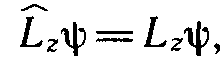
или

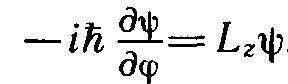
имеет частные решения вида

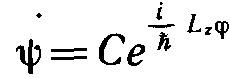
Поскольку полный обход вокруг оси Oz при изменении угла φ на 2π приводит нас в исходную точку пространства (r и θ постоянны), то из условия однозначности решения следует равенство

ψ(φ+2π) = ψ(φ)

Оно удовлетворяется, если положить

L_z=mћ, m = 0, ±1, ±2,... (10.12)

После нормировки и подстановки L_z собственные функции оператора L_z принимают вид

(10.13)

Часто используются названия: для l — азимутальное, или орбитальное, квантовое число; для m — магнитное квантовое число.

Из формул (10.8) и (10.13) видно, что сферические функции являются общими собственными функциями как оператора L², так и оператора L_z. Кроме того, из выражения (10.9) следует, что состояния с заданными моментом и его проекцией L_z возможны, если

l >~ |m|. Физически это условие вполне очевидно, так как проекция по модулю не может быть больше модуля вектора. Итак, m принимает 2l+ 1 значение:

m = 0, ±1, ±2,.., ±l.

В целях наглядности результаты квантования момента импульса и его проекции отображают в чертежах, подобных рисунку 10.1. Данные рисунка соответствуют значению 1 = 2. Радиус полуокружности равен (в принятом масштабе) L, т. е. ћ√6. Следует помнить об условном характере таких рисунков: по аналогии с классикой принято сопоставлять состояниям с одним / и разными пг различные определенные ориентации вектора момента импульса, хотя две другие проекции и не имеют определенного значения.

В приложениях часто применяется полуклассическая векторная модель момента импульса (рис. 10.2). Считается, что вектор момента импульса быстро вращается (прецессирует) вокруг оси Oz,

сохраняя свой угол наклона к оси (см. ч. I, пример 17.3). Для подобной классической системы величина момента и проекция L_z являются интегралами движения. Значения L_x и L_y непостоянны, а средние значения этих величин равны нулю. Сходство с квантовыми системами

2Ь

L--h<fb

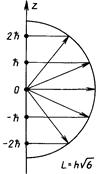
Рнс. 10 1.

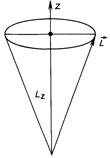
Рнс. 10 2.

здесь в том, что имеется определенное значение момента и его проекции L_z и равны нулю средние значения L_x и L_y.

Очень важное различие квантового и классического моментов импульса заключается в том, что отношение L_z/L (косинус угла наклона) в квантовом случае принимает дискретный ряд значений. Этот факт получил название пространственного квантования. Он может быть учтен в рамках векторной модели с помощью дополнительного положения о дискретном наборе ориентации вектора L по отношению к оси Oz. (Заметим, что момент импульса не может быть направлен точно по оси.) Выбор оси Oz в свободном пространстве, разумеется, совершенно произволен. Однако если некоторое направление в пространстве физически выделено, то направление оси Oz совпадает с ним.

Date: 2015-05-19; view: 1184; Нарушение авторских прав