Угловое и радиальное распределение плотности электронного облака

В предыдущем параграфе решено уравнение для движения электрона в кулоновском поле. Результаты решения дают возможность сделать заключение о пространственной структуре и других характеристиках атома водорода.

Запишем выражение для вероятности обнаружения электрона в элементе объема

(dV=r² sin θdrdθdφ)

вблизи точки с координатами

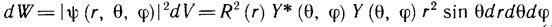
(12.1)

(Квантовые числа для сокращения записи опущены.) Распределению вероятностей (12.1) сопоставляется представление об электроне в виде облака, имеющего плотность,

пропорциональную квадрату модуля волновой функции. При этом величина -е |ψ|²

рассматривается как плотность заряда электрона, непрерывно распределенного в пространстве. (Иногда используется следующая корпускулярная интерпретация строения атома: считается, что электрон быстро обегает пространство, занятое атомом, причем

время его пребывания в объеме dV пропорционально |ψ|²)

Конфигурация электронного облака задает пространственную структуру атома

Ввиду сложности волновой функции целесообразно рассмотреть сначала радиальное распределение плотности облака, а затем — угловое.

Рассчитаем с помощью выражения (11 21) вероятность обнаружения электрона в шаровом слое между сферами радиусом r и r+dr. Для этого проинтегрируем распределение (12.1) по углам θ и φ в полном интервале изменения этих переменных. Получим

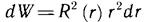
Плотность вероятности для значений координаты r описывается функцией

. (12.2)

Далее можно воспользоваться найденными ранее выражениями (11.11) для R_nl и найти зависимость плотности электронного облака от расстояния до центра атома для различных состояний.

Диаграммы для w_nl, w₂₀, w₂₁ представлены на рисунке 12 1.

Очевидно, что вблизи ядра и на больших расстояниях от него вероятность обнаружить частицу весьма мала. Плотность облака значительна на конечных расстояниях от начала координат. Здесь функция w_nl(r) обращается в нуль n – l -1 раз, и облако разбивается на слои

Вычисление средних расстояний приводит к формуле

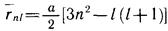
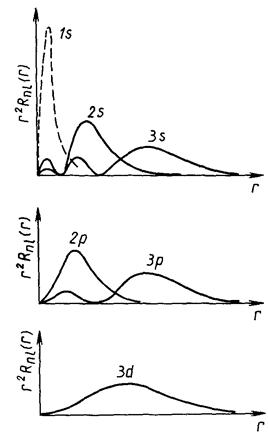
Рис 12 1.

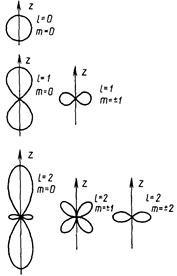
Рис. 12.2

r_nl быстро растет при увеличении главного квантового числа, а при заданном n убывает с ростом орбитального квантового числа l.

Резкой границы у атома нет. Однако плотность электронного облака очень быстро (экспоненциально) спадает при r>r. При r->оо вероятность обнаружить электрон практически равна нулю.

В состояниях с l = n-1

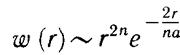
и максимум функции w (r) в этом случае достигается в точке r = аn². Эти расстояния совпадают с боровскими радиусами круговых орбит.

Перейдем к угловому распределению электронного облака. Согласно формулам (12 1) и (11.10) вероятность обнаружения частицы в пределах элементарного телесного угла dΩ, равного sin θdθdφ и взятого в направлении, заданном углами θ и φ, определяется формулой

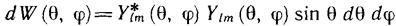
d W (θ, φ)= Y^* _lm (θ, φ) Y_lm (θ, φ) sin θ dθ dφ.

Соответственно плотность вероятности

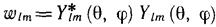
w_lm = Y^* _lm (θ, φ) Y_lm (θ, φ). (12.3)

Поскольку зависимость функции Y_lm от угла φ имеет вид е^imφ то плотность вероятности углового распределения не зависит от φ, что указывает на осевую симметрию электронного облака.

Распределение по полярному углу θ часто представляют графически в виде полярных диаграмм. Они строятся следующим способом.

На координатной прямой г полярной системы координат от точки 0 откладывается значение w_lm (θ). Через полученные точки проводится линия. Чем дальше точки кривой отстоят от начала координат, тем больше вероятность обнаружить частицу в заданном направлении.

Рассмотрим в качестве примера три состояния (см. формулы (10.11)):

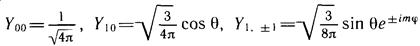
Соответствующие полярные диаграммы изображены на рисунке 12.2. В s-состояниях облако имеет сферическую симметрию. В р-состояниях при m = 0 оно вытянуто вдоль оси Oz, а при m=±1 облако сгущается в экваториальной плоскости. На полярной оси вероятность нахождения частицы равна нулю.

Мы предлагаем читателю в качестве упражнения свести воедино радиальное и угловое распределения для электронного облака в состояниях 1s, 2s и 2p(m = 0, ±1): изображение атома в разных состояниях показано на переднем форзаце.

Для больших значений пи/ строение атома водорода оказывается довольно сложным. Для ознакомления с этим вопросом следует обратиться к более детальным руководствам или справочникам (см. [21]).

12.2. «Вращение» электронного облака.

Неравный нулю момент импульса указывает на вращение электрона вокруг ядра. Движение частицы легко представить в рамках классического корпускулярного подхода, однако у электрона определенной траектории и скорости нет. При классическом волновом подходе частице сопоставляется облако, которое сложным образом, отнюдь не как единое

целое совершает вращательное движение. Величина, которая на квантовом языке характеризует движение микрочастицы, есть вектор плотности потока вероятности.

Для его вычисления используем формулы (2.3), (315) и выражение для оператора V в сферических координатах:

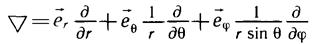
Если волновая функция имеет вид

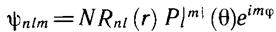
то следует принять в формуле (3.15):

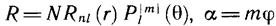
Массу частицы примем равной μ. Тогда получаем

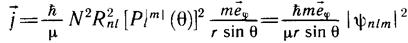
(12.4)

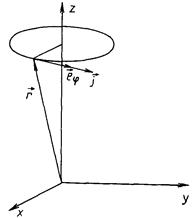
Рис 12 3

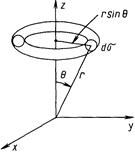
Рис 12 4

Линии вектора j есть замкнутые окружности с центрами на оси Oz (рис. 12.3). Они лежат в плоскостях, параллельных плоскости хОу. Во всех точках окружности модуль вектора один и тот же. Это следствие осевой симметрии и стационарности плотности облака; при вращении его конфигурация не изменяется.

В соответствии с классическим образом электронного облака плотность потока массы в нем пропорциональна плотности облака, но коэффициент пропорциональности в формуле (12.4) - величина, зависящая от переменных r и θ. Это значит, что облако вращается не как одно целое; скорости зависят и от расстояний до ядра r, и от угловой координаты пояса θ.

Б заключение вопроса о форме и размерах электронного облака, вращении его следует заметить, что все сказанное выше имеет условный характер и не должно пониматься в буквальном смысле классического объекта с непрерывно распределенными по пространству массой и зарядом. Облако лишь наглядная модель статистической трактовки функции состояния.

Мы рассматривали атом водорода, но в общих чертах полученные результаты относятся не только к водородоподобным системам, но и к многоэлектронным атомам, ибо в них в первом приближении электроны описываются используемыми выше функциями

состояния.

Date: 2015-05-19; view: 1577; Нарушение авторских прав