Пример 9.1. Использование теорем Эреифеста

Рассмотрим переходит квантового уравнения (9.14) к основному закону клас-

классической механики в случаях, когда средние значения имеют смысл. Для этого пред-

представим себе, что волновая функция заметно отлична от нуля лишь в малой области

пространства Дх. Как известно из § 4, п. 2, такое состояние описывается

волновым пакетом. Значение х можно принять равным координате середины пакета.

Если Дх мало, то

Fx(x)~Fx(x). (9.15)

Поскольку сила определяется градиентом потенциальной энергии, равенство (9.15)

выполняется с достаточной точностью только в медленно и плавно изменяющихся

полях. Наш случай тоже относится к плавным полям.

Если учесть соотношение (9.15), то иа основании формулы (9.14) имеем

mx = Fx(x).

95Это по форме уже классическое соотношение, так как при малом Дх пакет

можно сопоставить материальной точке. Однако условие (9.15) еще недоста-

недостаточно для перехода к классической механике, так как частица должна иметь

определенный импульс.

Пакет образуется набором монохроматических волн с импульсами, лежащими

в интервале р±Ар. Если

Др<р, (9.16)

то можно положить р«р. Условие (9.16) заведомо выполняется, если кинетичес-

кинетическая энергия достаточно велика, так как правую часть равенства можно сделать

сколь угодно большой, увеличивая энергию частицы.

Таким образом, квантовое движение приобретает классические черты при пе-

переходе к большим энергиям в плавно изменяющихся силовых полях.

Вопрос разобран еще не до конца. С течением времени пакет расплывается,

Ах растет н, вообще говоря, соответствие классической картине движения

теряется.

Можно показать, что время, за которое ширина пакета удваивается, по порядку

величины равно:

где при вычислении нужно взять начальное значение Ах. Для частиц атомных размеров

масса /л~10~27 кг, Дх~10~10 м и формула (9.17) дает <~10~'3 с. В газе при

нормальных условиях среднее время свободного пробега ~ 10~'° с, поэтому представ-

представление о молекулах газа как о классических корпускулах, вообще говоря, является

неправомерным. Из соотношения (9.17) следует, что переход к классической меха-

механике есть переход к частицам достаточно большой массы.

9.4. Законы сохранения физических величин в квантовой меха-

механике. Как и в других разделах физики, в квантовой механике важней-

важнейшее значение имеют законы сохранения ряда динамических величин,

характеризующих состояние микрочастицы или системы микро-

микрочастиц и изменение этого состояния. Таковы законы сохранения

энергии, импульса, момента импульса — величин, имеющих универ-

универсальное применение во всей физике. В микромире к ним добавляется

закон сохранения четности — величины, специфической для кван-

квантовой физики (и ряд других—см. [19]).

В классической механике и электродинамике законы сохранения

получают, преобразуя основные уравнения теории — уравнения

Ньютона, Максвелла. Из них получают законы изменения с те-

течением времени импульса, момента импульса, энергии, а затем

рассматривают специальные условия, при которых данные величины

не изменяются во времени, т. е. сохраняются. Этими условиями

служат замкнутость и изолированность изучаемой системы: в ме-

механике — тел, в электродинамике — поля и заряженных тел.

Аналогичен подход к законам сохранения во времени и в кванто-

квантовой механике. Уравнение Шредингера привело нас к формуле (9.4)

для оператора производной физической величины по времени:

А=§+±[Н, А].

Применяя его для вычисления производной по времени от среднего

значения величины, заключаем, что при условии Л = 0, a = const,

среднее значение физической величины сохраняется во времени.

96Рассмотрим условия сохранения определенного значения фи-

физической величины. Если функция состояния г|), в котором находится

система, совпадает с собственной функцией ф, оператора А, то вели-

величина имеет определенное значение: щ. Из формулы для среднего

(8.7) в этом случае получаем а = щ. Если, кроме того, оператор

(9.4) равен нулю, то определенное значение сохраняется. (Вели-

(Величина а, является интегралом движения.)

Закон сохранения энергии. Оператор Гамильтона мо-

может зависеть от времени, но может и не зависеть от него. Во

всех решенных ранее задачах встречались стационарные поля, для

них <Ш.= 0. Кроме того, очевидно, что [Я, #] = 0. Следовательно,

# = 0, а Е = const.

Если функция состояния системы в стационарном поле соб-

собственная для оператора Гамильтона, то энергия имеет определен-

определенное сохраняющееся значение. О таких состояниях уже говорилось

ранее как о стационарных.

Энергия микрочастицы в стационарном поле сохраняется.

Понятно также, что оператор Гамильтона для свободной час-

частицы не содержит времени: энергия свободной частицы — величина

постоянная. Осталось рассмотреть весьма важный случай замкну-

замкнутой системы частиц. Замкнутость означает учет всех взаимо-

взаимодействующих частиц, т. е. потенциальная энергия зависит от

расстояний между ними (см. ч. I, § 14, п. 6), гамильтониан системы

не содержит времени. Поэтому энергия замкнутой системы микро-

микрочастиц сохраняется.

Закон сохранения импульса. Оператор импульса

л

частицы: р = —lh V — не содержит времени и коммутирует с опера-

оператором Гамильтона для свободной частицы: #=—— А.

2т

Следовательно, импульс свободной микрочастицы сохраняется.

Если частица находится в силовом поле, то оператор Га-

Гамильтона содержит координаты, на которые действует опера-

тор импульса, т. е. р и Н не коммутируют в общем случае. В силовом

поле импульс не сохраняется.

Для замкнутой системы частиц доказывается (см. § 9, п. 6),

что оператор импульса коммутирует с оператором Гамильтона —

импульс замкнутой системы микрочастиц сохраняется.

Закон сохранения момента импульса. Оператор

момента импульса для частицы:

L = — ih[rV]

не содержит времени и коммутирует с оператором Гамильтона сво-

свободной частицы. Следовательно, момент импульса свободной час-

частицы сохраняется (т. е. существуют состояния, в которых он

постоянен наряду с энергией).

В общем случае в силовом поле момент импульса не сохраняется,

4 Заказ 891 97однако, как и в классической механике, здесь имеют место важные

частные случаи. В центрально-симметричном поле, например, мо-

момент сохраняется. (Особенности квантового случая по сравнению с

классическим рассматриваются ниже, в главе IV.)

Оператор момента импульса для системы частиц коммутирует

с оператором Гамильтона для замкнутой системы, поэтому момент

импульса замкнутой системы микрочастиц сохраняется (см. § 9,

п. 6).

Итак, законы сохранения энергии, импульса, момента импульса

в квантовой механике по форме и содержанию аналогичны класси-

классическим.

Связь законов сохранения с инвариантностью оператора Гамнльтоиа

относительно преобразований симметрии.

Покажем, что законы сохранения физи-

физических величин связаны со свойствами симметрии пространства н времени. Здесь

и далее под симметрией понимается неизменность свойств пространства при сдвигах,

поворотах, отражениях, приводящая к инвариантности некоторых величин и выраже-

выражений относительно соответствующих преобразований координат.

В основном уравнении квантовой механики — уравнении Шредингера — система

представлена через оператор Гамильтона. Поэтому симметрия системы проявляет-

проявляется в инвариантности гамильтониана относительно каких-либо преобразований

координат и времени.

Рассмотрим некоторое преобразование координат:

г-*?, (9.18)

выражающее либо перемещение системы как целого в пространстве — сдвиг, либо

поворот, либо отражение в зеркале. Его удобно записать на операторном языке

так:

? = §;. (9.19)

Обратное преобразование выражается оператором S~{. Последнее означает, что

7=s~1?.

Пусть состояние системы описывалось до перемещения функцией tip (r). Произ-

Произведем преобразование (9.19), которое изменит и г, и вид \(>. Но если существует

соответствующая симметрия пространства, то в точку 7' перейдет значение волновой

функции, ранее бывшее в точке г. Поэтому новая волновая функция / (/•') удовлет-

удовлетворяет равенству

fG') = f(S7) = qG). (9.20)

Введем оператор R, изменяющий внд функции в рассматриваемом преобра-

преобразовании:

R*(r) = f(r). (9.21)

где R может быть оператором преобразования для сдвига, поворота и отражения

системы в зеркале.

Докажем, что если гамильтониан инвариантен относительно преобразова-

преобразования (9.19), то оператор R коммутирует с оператором Гамильтона. Согласно форму-

формулам (9.20) и (9.21)

R^G) = ^(S-I7). (9.22)

Введем обозначение 7" = S~*7для результата преобразования в равенстве (9.22).

Тогда для произвольной функции ф имеем

Если НG) = Н(г"), т. е. преобразование S не изменяет гамильтониан, то правые

части равенств совпадают. Следовательно, RH — HR. Утверждение доказано.

98Если оператор физической величины не зависит от времени и коммутирует

с гамильтонианом, то эта физическая величина сохраняется. Коммутативность

операторов R и Н означает наличие закона сохранения величины Ц. Чтобы указать

ее физический смысл, нужно задать явный внд оператора R.

Во многих случаях конечное преобразование координат можно представить

как совокупность последовательных бесконечно малых преобразований. Рассмотрим,

например, бесконечно малый сдвиг — трансляцию системы в пространстве:

r' = r+6r.

Обратное преобразование:

г = г' — 6г.

С точностью до членов второго порядка малости:

у (S"'г) = у {г — Ьг)«* (г) — Ьг VЧ>-

Согласно соотношению (9.22)

Отсюда _

й = 1—6rV.

Это оператор бесконечно малого смещения (сдвига или трансляции) в про-

пространстве.

9.6. Связь законов сохранения импульса, момента импульса н энергии со свой-

свойствами пространства и времени. Пусть преобразование координат есть сдвиг на

отрезок а:

г' = г + а. (9.23)

Вследствие однородности пространства состояние замкнутой системы не должно

изменяться при сдвиге. Это обусловливает выполнение равенства (9.20).

Как будет показано в дальнейшем, оператор Гамильтона для системы частиц

имеет вид N

Н= 2 -£L-+U(?U 72,.... 7N), (9.24)

где р,■ — операторы импульсов отдельных частиц, р,-=— ihv,, V,=T \-Т h

- д dxi ' ду<

+*-^-, a U(ru г2 гн) — потенциальная энергия их взаимодействия. Все извест-

известные типы взаимодействия между частицами таковы, что потенциальная энергия

зависит только от расстояния между частицами. Поэтому оператор (9.24) не меня-

меняет вида, если сделать замену переменных (9.23).

Оператор бесконечно малого смещения R в данном случае имеет вид

JV. Л

R=\—ba 2 Vi=\—~6ap,

l—i П

ГДе * * А

Р= 2 pi (9.25)

i=i

— оператор импульса системы.

Из коммутативности оператора импульса (9.25) с оператором Гамильтона (9.24)

следует закон сохранения импульса замкнутой системы.

Может показаться, что операторы р и Н не коммутируют вследствие наличия

в гамильтоннане слагаемого, соответствующего потенцнальной энергии. Но это не так.

Для системы нз двух частиц U (?,, г2)=1/ (г), где г=У(х2— Xlf + (y2— y,f + (z2 — z,f.

Найдем коммутатор [рх, U]:

-• U,+£

99дг дг

В результате получаем нуль, так как -т—=-з—■

Вывод закона сохранения импульса с учетом однородности пространства рас-

раскрывает в определенном отношении природу импульса: импульс можно ввести как

величину, сохраняющуюся в силу однородности пространства.

При повороте системы вокруг некоторой оси на бесконечно малый угол бф

всякая точка смещается на отрезок

В этом случае

Я = 1— [6ф7] V.

Используя свойства смешанного пронзведения векторов, получаем ■

R = 1 —6ф [г V ]= 1 —у бфГ,

где L — оператор момента импульса частицы.

Состояние замкнутой системы, а значит, и ее гамильтониан не изменяются при

поворотах вокруг осн вследствие изотропии пространства; следовательно, оператор

R коммутирует с Н, что приводит к коммутации L н Н. Отсюда вытекает закон сохра-

сохранения момента импульса.

Математическая сторона вопроса о наличии интегралов движения мало изме-

изменится, если вместо координат речь пойдет о каком-нибудь параметре, входящем

в гамильтониан. В частности, таким параметром является время.

Введем оператор т смещения во времени на интервал т:

t' = xt = t + x.

Оператор, действующий на функцию tip прн сдвиге во времени, обозначим

через Т. В соответствии с выражением (9.22) имеем

fi|> = i|>(f—г).

Найдем конкретный внд оператора Т для сдвига на бесконечно малый промежуток

времени 6т:

Если воспользоваться уравнением Шредингера (8.3), то можно выразить из него

д

оператор -^-, после чего получим

Если оператор Н не зависит от времени, то операторы Т н Н коммутируют. Для

замкнутой системы оператор Гамильтона не зависит от времени, энергия сохра-

сохраняется.

Существенно, что энергия как физическая величина связана с однородностью

времени, ибо ее сохранение обусловлено однородностью времени.

9.7. Четность и закон сохранения четности. Кроме однородности

и изотропности, имеется еще один вид симметрии пространства;

соответствующую ему операцию нельзя свести к совокупности беско-

бесконечно малых преобразований координат. Речь идет об операции

инверсии, заключающейся в изменении знака всех трех координат

х, у и z:

;-?=-;, (9.26)

или

х'=—х, у' = —у, z' = —z.

100

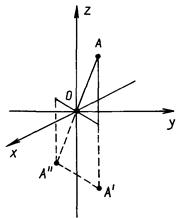
Рис 9 1

Э

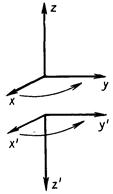
Рис 9 2.

Операцию инверсии можно провести в два этапа, комбинируя

отражение в зеркале и поворот на угол 180°. На рисунке 9.1 точка А

при отражении в зеркале, поверхность которого совпадает с плос-

плоскостью хОу, переходит в точку А'. Если совершить еще и поворот

вокруг оси Oz, то точка А' совместится с точкой А", координаты

которой связаны с координатами точки А преобразованием инверсии.

Поэтому симметрия систем относительно инверсии непосредственно

связана с симметрией относительно отражения в зеркале — с сим-

симметрией «правого» и «левого».

Всякое преобразование координат можно трактовать двояко: как

следствие перемещения системы (при неизменных осях координат)

и как следствие изменения положения осей координат (при этом

физическая система остается неподвижной). До сих пор мы исполь-

использовали только первый способ. Однако второй способ эквивалентен

первому. При нем преобразование (9.26) рассматривается как из-

изменение направления осей координат: правая декартова система

координат переходит в левую. Это показано на рисунке 9.2.

Предположим, что состояние физической системы не изменяется

при инверсии. Пусть до преобразования она описывалась волновой

функцией г|5 (г). Волновая функция / (г'), описывающая систему пос-

после преобразования, должна удовлетворять равенству

*(?) = f(?') = f{-r)- (9.27)

Введем оператор, изменяющий вид функции при изменении знака

у координат, и назовем его оператором инверсии:

Согласно равенству (9.27) имеем

= f (?) = *(-?). (9.28)

Если оператор Р коммутирует с гамильтонианом, то существует

101

закон сохранения некоторой физической величины, которая получила

название четность. Для указанной коммутации оператор Гамильтона

системы должен быть инвариантным относительно инверсии коорди-

координат, а это его свойство вытекает из предположения, что состояние

физической системы не изменяется при инверсии.

Для определения допустимых значений четности запишем урав-

уравнение для собственных функций и собственных значений оператора

инверсии:

= рФ(г) (9.29)

Применяя опера-тор Р к обеим частям соотношения (9.29), полу-

получим

Р\{г) = р\(Р). (9.30)

Но согласно определению оператора инверсии (9.28) последователь-

последовательное применение его к любой функции дважды даст исходную функ-

функцию:

Я(ЯФ(^) = ЯФ(-?) = Ф(;). (9.31)

Сравнивая уравнения (9.30) и (9.31), находим, что р2=1, ар =

= ±1—собственные значения оператора инверсии: +1 и —1.

Эти два числа и принимаются за значения новой физической

величины — четности состояния микрочастицы или системы микро-

микрочастиц.

Если функция состояния не изменяется при инверсии осей, то

состояние четное, а четность равна +1; если изменяет знак — не-

нечетное, четность — 1.

В отличие от аддитивных сохраняющихся величин, рассмотрен-

рассмотренных ранее, четность—величина мультипликативная, т. е. четность

системы равна произведению четностей ее частей. Это становится

понятным, если, забегая вперед, сообщить, что функция состояния

системы невзаимодействующих частиц равна произведению одно-

частичных функций:

Если Я и Я коммутируют, то существуют состояния с определен-

определенной энергией и определенной четностью. В качестве примера укажем

на найденные ранее состояния гармонического осциллятора и части-

частицы в прямоугольной потенциальной яме с бесконечно высокими

стенками: четность стационарных состояний имеет определенное,

не изменяющееся во времени значение — плюс или минус единица.

Все гамильтонианы электромагнитных взаимодействий не изме-

изменяются при пространственной инверсии, поэтому справедлив закон

сохранения четности замкнутой системы при электромагнитных

взаимодействиях в ней.

Мы рассмотрели четность состояния микрочастиц, обусловленную

пространственным движением, описываемым волновой функцией.

Однако результаты анализа многочисленных экспериментов —

реакций с элементарными частицами — на основании закона со-

сохранения четности заставляют приписывать элементарным частицам

102собственные (внутренние)' значения четности, не связанные

с движением частиц в пространстве. Так, например, электронам,

нейтронам, протонам следует приписать внутреннюю четность +1,

а пи-мезонам и позитронам — четность —1. Фотоны же могут иметь

ту и другую четность.

В классической физике понятие о четности состояния не рас-

рассматривается в связи с тем, что изменение направления осей ко-

координат не приводит в силу применяемого там способа описания

движений и взаимодействий к новой сохраняющейся величине.

В квантовой механике понятие о четности возникает в связи с

описанием состояния с помощью ■ф-функции, а закон сохранения

четности наряду с законами сохранения энергии, импульса, мо-

момента импульса оказывается связанным с фундаментальными

свойствами пространства.

Рассматривая условный выбор либо «правой», либо «левой»

систем, нет никаких оснований ожидать, что от этого выбора могут

зависеть свойства изучаемых физических объектов — замкнутых

систем микрочастиц. Однако возможен и другой взгляд на пре-

преобразования инверсии: можно предположить, что существуют два

вида пространства — «правое» и «левое», не эквивалентные друг

другу; связь между ними отражена в формулах инверсии осей

координат. В таком случае гамильтонианы необязательно ком-

коммутируют с оператором инверсии и четность может не сохраняться.

В 1956 г. было обнаружено, что процессы распада ядер и элементар-

элементарных частиц, происходящие за счет слабого взаимодействия, про-

происходят с нарушением закона сохранения четности. В настоящее

время экспериментально подтверждено, что четность сохраняется

в электромагнитных и сильных взаимодействиях и не сохраняется

в слабых. Но до сих пор не вполне ясно, обусловлено ли нарушение

закона сохранения четности только фундаментальными свойствами

пространства и времени или связано с другими причинами.

Date: 2015-05-19; view: 513; Нарушение авторских прав