Анализ решения задачи о гармоническом осцилляторе

Условие (6.13) задает правило квантования энергии осциллятора.

Если учесть подстановку (6.5), то

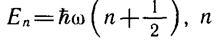
, n = 0, 1, 2,... (6.18)

Это одна из самых фундаментальных формул квантовой физики.

Из нее прежде всего следует дискретный набор значений энергии, обычно называемых уровнями. Интервал между соседними уровнями постоянен и равен ћω, поэтому переходы между ними обеспечивают излучение или поглощение одинаковых квантов энергии. Если этим квантам сопоставляется макроскопическое волновое поле, например

электромагнитное, то частота его и определяется формулой Планка (1.3). Таким образом, гипотеза Планка оказалась прямым следствием общих принципов квантовой механики.

Далее, наименьшее возможное значение энергии равно ћω/2 это энергия так называемых нулевых колебаний. Как и в прямоугольной яме, уровни осциллятора начинаются с некоторого отличного от нуля минимального значения.

С энергией нулевых колебаний: Е₀= ћω/2—связан целый ряд физических явлений. В частности, она свидетельствует об отсутствии покоя у частиц вещества при абсолютном нуле температуры. На ее основе сложилось представление о нулевых колебаниях вакуума как об основном (невозбужденном) состоянии электромагнитного поля и т. д.

Рассмотрим несколько функций состояния квантового осциллятора, соответствующих энергиям Е₀= 1/2 ћω, Е₁=3/2 ћω, E₂ = 5/2 ћω и т. д. С помощью формул (6.15)... (6.17), а также возвращаясь к исходной переменной х на основе соотношения (6.3), получаем

60(x)=- \l/2 ' (6.19)

i4i~2)-

6.1

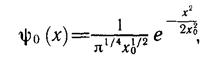
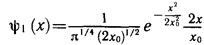
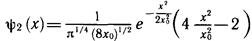
На рисунке 6.2 показаны соответствующие диаграммы плотности вероятности. Вертикальные линии проведены через точки, соответствующие амплитудным значениям координат классического осциллятора с рассматриваемыми энергиями Е₀, Е₁ Е₂. Штриховые кривые изображают классическую плотность вероятности как отношение времени нахождения материальной точки в данном месте пространства к периоду колебаний. Из формул (6.19) также видно, что четность состояния определяется четностью квантового числа n: при четных n четность равна +1, а при нечетных -1.

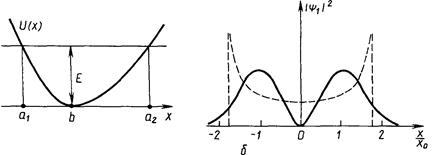
Уместно изобразить еще уровни энергии осциллятора на диаграмме его потенциальной энергии (рис. 6.3) Если сравнить эту диаграмму с диаграммой рисунка 5.3 для потенциальной ямы, то становится очевидной зависимость расстояний между уровнями от формы потенциальной кривой.

На примере разобранных одномерных задач можно указать на некоторые общие особенности квантово-механического движения.

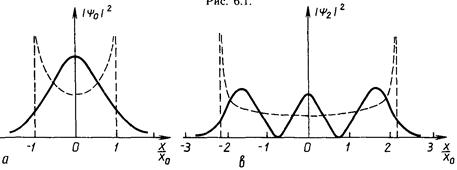Рис. 6.2.

6.2

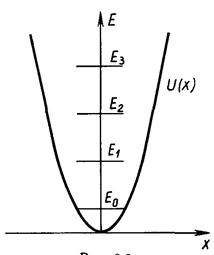
Рис. 6.3.

Рис. 6.4.

1. В постоянных полях типа потенциальной ямы возможны стационарные состояния с дискретными уровнями энергии.

2. У таких систем наименьшее значение энергии отлично от нуля, что соответствует невозможности абсолютного покоя и локализации частиц в точке пространства.

3. Квантование энергии характерно для связанных состояний.

Для несвязанных частиц движение инфинитно, и энергия принимает

непрерывный ряд значений.

4. Как координата, так и импульс в связанных состояниях неопределенны, а это значит, что подразделить энергию на кинетическую и потенциальную невозможно.

5. Квантовые частицы способны проникать в области пространства, недоступные для классических частиц.

Date: 2015-05-19; view: 678; Нарушение авторских прав