Разложение функций в обобщенный ряд и интеграл Фурье

Применение принципа суперпозиции состояний (см. § 2, п. 4) в квантовой механике тесно связано с разложением функций в ряд или интеграл Фурье. Напомним основные математические положения о разложениях функций. Пусть задана функция φ = φ (k, x), причем k есть дискретно изменяющаяся величина, играющая роль параметра,

а под х понимается совокупность трех координат точки пространства. Если значения k пронумеровать в определенном порядке, то можно рассматривать систему функций, в которой функции можно различать по номеру и писать φ_k (х) вместо φ(k, х), причем k = 1, 2, 3

и т. д.

Система функций φ_k (х) называется ортонормированной, если все функции

φ_k(х) нормированы на единицу и попарно ортогональны.

Условие ортонормированности выражается соотношением

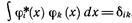
\ (р?(х) ср* (x) dx = 6ik,

где δ_ik — символ Кронекера (δ_ik = 0 при I /=к и δ_ik =1 при i = k).

Система φ_k(х) называется полной, если не существует функции, ортогональной ко всем функциям системы и не входящей в эту систему.

Допустим, что в интервале а < х < b задана полная ортонормированная система функций φ_k(х). Тогда любая непрерывная однозначная ограниченная и квадратично-интегрируемая в интервале (а, b) функция ψ(х) может быть представлена в виде ряда

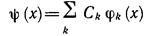
1К*) = 2с*ф*(ж), G.1)

к

где числа С_к определяются формулой

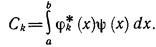
ь

Они называются коэффициентами Фурье, а ряд G.1) — обобщенным

рядом Фурье. Этот ряд в указанном интервале сходится, и сходится к

функции г|> (х) (за исключением конечного числа изолированных

точек, к которым относятся точки разрывов непрерывности, концы

интервала и др.).

Пусть имеется система функций ср (k, x) с непрерывно изменяю-

изменяющимся параметром k. Она называется ортонормированной или нор-

нормированной на б-функцию (сведения о б-функции приведены в при-

приложении I), если выполняется соотношение

*(k\x)(f(k,x)dx = 8(k' — k). G.2)

Ортонормированная система ср (k, x) называется полной, если не

существует функции, ортогональной ко всем функциям системы и не

входящей в эту систему.

Произвольную непрерывную и квадратично-интегрируемую

функцию г|з (х) можно представить в виде интеграла Фурье:

Ъ {х) = \ С (k) у {k, x) dk, G.3)

где коэффициент Фурье С (k) находят по формуле

Интеграл G.3) для полной системы функций ср (k, x) сходится,

и сходится к функции г|> (х) (везде, кроме ограниченного числа изо-

изолированных точек).

Из математики известны условия полноты системы функций tp (k, x):

2 <f'k(x')yb{x) = b(x— x'). G.3а)

71Для системы функций с непрерывно изменяющимся параметром k условие

приобретает вид

\ <р* (*, х') Ф (k, х) dk = 6(x—x'). G.3 б)

В самом деле, подставляя в формально написанное равенство G.1) коэффи-

коэффициенты Фурье Ск, получаем

ь

\

Отсюда для выполнения равенства G.1) достаточно выполнения условия G.3 а).

(Так же доказывается и условие G.3 6).)

Можно дать и иную трактовку сходимости разложений G.1) и G.3). Равен-

Равенство G.1) имеет смысл, т. е. справедливо, если квадратичная погрешность разложе-

разложения равна нулю:

) I ф(*) —2iC*<p*(je) I dx = Q.

а

Отсюда иемедлеиио следует достаточное условие справедливости равенства G.1):

ь

^C\Ck = \^'{x)^{x)dx. G.3 в)

а

Аналогично для разложения G.3) имеем

\ С (ft) С (ft) dkJ\ V (х) Мр (х) dx. G.3 г)

Условия G.3 в) и G.3 г) также необходимы, т. е. для полной

системы функций ф* (х) и непрерывной ty (x) всегда выполняются.

Установим связь разложений функций с принципом суперпозиции

состояний. Пусть г|з (х) есть волновая функция состояния некоторой

механической системы. Разложим ее в ряд по функциям ср* (х). На

основании равенства G.1) или G. 3) состояние ty может рассматри-

рассматриваться как суперпозиция состояний ср* (или ср (k, x)) с вероятностями

ClCk (или плотностью вероятности C*(k)C(k)). Такой смысл при-

придается разложению функции состояния в обобщенный ряд или

интеграл Фурье: оно выражает суперпозицию состояний.

Как указывалось ранее (§ 2), волновые функции суть комплексные непрерывные однозначные функции от координат и времени.

Как правило, они квадратично-интегрируемые, т. е. не только везде ограничены по модулю, но и достаточно быстро убывают до нуля на бесконечности, что и обусловливает возможность их использования для описания связанных состояний микрочастицы в

ограниченной (и в большинстве случаев очень малой) области пространства.

Но эти же свойства необходимы и для разложений в ряд или интеграл.

В квантовой механике используются и функции, ие являющиеся квадратично-

интегрируемыми Не удовлетворяет этому условию \|)-функция свободной частицы

(§ 3, п. 5) Эта и некоторые другие подобные ей функции фактически не отвечают

реальным физическим состояниям, реальным объектам, а описывают сильно идеали-

идеализированные модели и играют вспомогательную роль. Так, для каждой микрочастицы

известна в конечном счете область локализации в пространстве — это может быть атом, молекула, макроскопическое тело и т. д. Локализованной частице соответствует уже ие плоская волна, а волновой пакет, т. е. быстро затухающая и квадратично-интегрируемая функция состояния. В каждом конкретном случае может быть выяснена роль функции, не удовлетворяющей условию квадратичной интегрируемости, и установлена ее связь с реальными состояниями.

Изучаемые ниже математические соотношения, в которые входят волновые функции, распространяются не только на квадратично-интегрируемые функции, но и путем соответствующих предельных переходов — на ограниченные (по модулю) функции, необязательно затухающие иа бесконечности.

Отметим также, что разложение функций состояний в ряд, а также все действия, которые производятся ниже над функциями с помощью операторов физических величин, не затрагивают переменную t — время, т. е. относятся к произвольному, но фиксированному

моменту времени. По этой причине время t всегда рассматривается как параметр, а переменные х, у, г — как аргументы ^-функции.

Date: 2015-05-19; view: 552; Нарушение авторских прав