Закон сохранения числа частиц

Сохранение вероятности можно трактовать как сохранение числа частиц. В наиболее

наглядной форме этот закон выступает, если допустить наличие в пространстве N независимых друг от друга одинаковых микрочастиц, находящихся в одном и том же квантовом состоянии.

Все частицы описываются одной и той же волновой функцией.

Если /V»l, то величина

равна плотности частиц в каждой точке пространства; интеграл

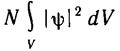v

определяет число частиц в объеме V; производная

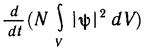
описывает изменение числа частиц в указанном объеме за единицу

времени. Интеграл

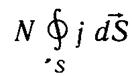
равен потоку частиц через поверхность, ограничивающую объем,

а вектор Nj есть плотность потока частиц. Поэтому равенство

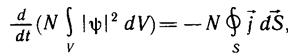, (3.14)

следующее из соотношения (3.13), выражает закон сохранения числа частиц в процессах, описываемых уравнением Шредингера:

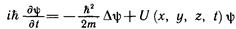
Стационарный вариант которого

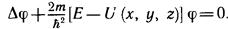
частицы не исчезают и не появляются в любой области простран-

пространства, они лишь могут входить в заданную область и выходить из

нее.

Произведение NjdS есть число частиц, проходящих в единицу

времени через площадку dS, поставленную перпендикулярно потоку.

Отношение

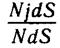
-£— определяет вероятность прохождения частицей

единичной по размерам площадки, поставленной перпендикулярно

потоку (за единицу времени). Мы видим, что указанная вероят-

вероятность равна модулю вектора плотности потока вероятности. Таким

образом, этот вектор может содержать непосредственную информа-

информацию о движении частицы.

В заключение данного пункта укажем полезное соотношение.

Любая комплексная функция может быть записана в виде (2.3):

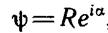
где R и а — действительные функции от координат и времени.

Мы предоставляем читателю возможность доказать, что функции

состояния B.3) соответствует вектор плотности потока вероятности:

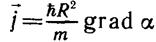. (3.15)

Формула (3.15) будет неоднократно использована в дальнейшем.

Date: 2015-05-19; view: 1589; Нарушение авторских прав