Гармонический осциллятор

6.1. Постановка задачи.

Гармонический осциллятор — это материальная точка, совершающая гармонические колебания, т. е. колебания, в которых смещение точки из положения равновесия изменяется по закону синуса и косинуса. Ясно, что такое кинематическое определение непригодно в квантовой области, где нельзя указать точного положения микрочастицы в пространстве. Более общим определением гармонического осциллятора, пригодным и в микромире, является динамическое определение.

Классический осциллятор — это материальная точка, движущаяся в силовом поле, в котором потенциальная энергия имеет минимум, как, например, на рисунке 6.1. В таком случае (см. ч. I, § 26)

малые отклонения частицы от точки устойчивого равновесия —минимума — приводят к гармоническим колебаниям. Приближенное значение потенциальной энергии, принимаемое в одномерном случае в расчет, следующее:

U = kx²/2, (6.1) ±

где k>0 — коэффициент квазиупругой силы.

Квантовый осциллятор — это частица, движущаяся в потенциальном поле с минимумом энергии. Если полная энергия частицы Е — величина малая, то потенциальную энергию можно выразить формулой (6.1). Коэффициент k удобно выразить через циклическую

частоту колебаний: ω = √(k/m). В таком случае вместо (6.1) имеем

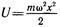
Последняя формула и определяет постановку задачи о квантовом гармоническом осцилляторе: это микрочастица, находящаяся в потенциальном поле вида (6.1).

Гармонические колебания играют очень важную роль в классической физике. Не менее важное значение имеет задача о гармоническом осцилляторе и в квантовой физике, где также говорят о гармонических колебаниях. Результаты ее решения средствами квантовой механики интересны как сами по себе, так и в качестве модельных представлений для реальных систем, в которых частица движется в силовом поле в окрестности точки минимума потенциальной энергии.

Date: 2015-05-19; view: 645; Нарушение авторских прав