Промежутке

Задана функция ψ = Се °, где С и а — константы, а r,— модуль радиус- вектора точки пространства. В этом случае

Г 2

\Се

Пример 2.3. Нормировка функций.

Условие нормировки

\ c2sin2 — dx=l

J "

о

/ 2

в примере B.1) приводит к равенству С=~\1—. Теперь функция

ψ = 2. лх

— sin —

а а

нормирована иа единицу.

Аналогично для примера 2.2 находим

г

2 —а

а3'2'

Пример 2.4. Использование плотности вероятности для оценки размеров атома.

Зависимость плотности вероятности местоположения электроиа от расстояния до

ядра в атоме водорода выражается формулой

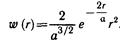
ω(r) = r

Ход кривой показан на рисунке 1.4.

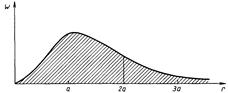
Из графика видно, что наибольшая вероятность соответствует расстоянию электрона до ядра: r = а = 0,5*10^~10 м. Имеется отличная от нуля вероятность обнаружить электрон и на больших расстояниях. Это значит, что резкой границы у атома нет, но вероятность обнаружения быстро спадает по мере роста r при r>а.

Чтобы определить вероятность нахождения электрона в сфере, ограниченной

радиусом 2а, необходимо определить площадь заштрихованной части графика до

точки r= 2а и найтн ее отношение ко всей площади под кривой w (r). Приблизнтельно получается 0,7. Обсудим смысл этой величины.

Для применения статистики нужно взять много атомов, находящихся в одном н том же состоянии, например 106 атомов. В этом случае наблюдается определенная закономерность: в 0,7-10⁶атомов в указанном объеме электроны обнаруживаютси, а

в остальных 0,3 -10⁶ атомов электроны обнаруживаются вне этого объема. В результате относительная погрешность предсказания тем меньше, чем больше берется атомов. Если же взят один атом или их небольшое число, то задание вероятности не

позволяет однозначно указать, находится электрон в заданном объеме или нет.

Существует также наглидная временная трактовка рассмотренного выше распределения вероятности для одного атома: электрон из какого-нибудь промежутка времени t (достаточно большого по сравнению с некоторым характерным временем — «периодом обращения» вокруг ядра) проводит 0,7t внутри указанного объема, а 0,3t — вне его.

Таким образом, размеры атома оцениваются по размерам его электронного

облака — области пространства с заметно отличной от нуля вероятностью обнаружения электрона. В ряде случаев оказывается возможным при взаимодействии электронов считать их заряды непрерывно распределенными по облаку с плотностью:

р = -eω,

где —е — электрический заряд электрона.

Разобранный пример 2.4 в какой-то мере отражает фактический предел той

степени наглядности, которая возможна при описании движения частицы с помощью

волновой функции. В рамках квантовой механики, в сущности, бессмысленно за-

задавать следующие вопросы: в какой точке находится частица, движущаяся с опре-

определенной скоростью? По какой траектории происходит ее движение? Чему равно

в данный момент значение ее координаты х? Природа такова, что на микроскопическом уровне достоверных ответов на такие вопросы получить нельзя. Можно только указать распределение вероятностей для координат и его изменение со временем, если плотность вероятности зависит от времени.

Date: 2015-05-19; view: 534; Нарушение авторских прав