Решение уравнения Шредингера для гармонического осциллятора

Запишем уравнение Шредингера для квантового гармонического осциллятора:

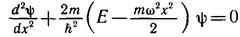. (6.2)

Здесь о» — частота колебаний классического осциллятора. С точки

зрения квантовой физики это некоторый параметр.

Начнем решение с замены переменных, что позволит упростить форму исходного уравнения (6.2). Введем безразмерную координату z:

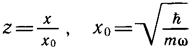(6.3)

После подстановки получаем уравнение

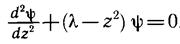, (6.4)

где

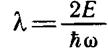
При |z| >> l постоянную λ в уравнении (6.4) можно опустить. Тогда

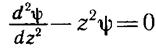
Если

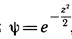, то

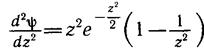
Отсюда видно, что экспонента

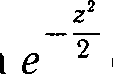
описывает асимптотическое решение уравнения (6.4) при z-> ±оо. Поэтому будем искать функцию состояния осциллятора в виде

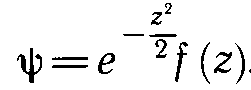. (6.6)

Функция f (z) удовлетворяет уравнению

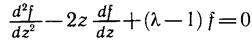
которое получается из уравнения (6.4) после подстановки функции (6.6).

Далее, используя метод степенных рядов, полагаем

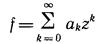
Подстановкой ряда (6.8) в уравнение (6.7) приходим к тождеству

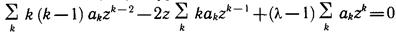. (6.9)

Его можно записать в виде одной суммы:

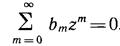. (6.10)

Для выполнения последнего равенства при любых z необходимо, чтобы были равны нулю коэффициенты при всех z^m. Составим выражение для коэффициента b_m. Для этого из первой суммы в равенстве (6.9) выпишем член с k= m + 2, а из второй и третьей — с

k = m.

Получаем

b_m =(m+2)(m+1)a_m+2 -2mа_m + (λ- 1)а_m . (6.11)

Приравнивая выражение (6.11) нулю, находим формулу, которой должны удовлетворять коэффициенты ряда (6.8):

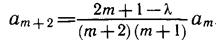
Формула (6.12) относится к рекуррентным соотношениям; она позволяет повторным применением выразить все коэффициенты а_m через первые два, которые остаются неопределенными. Величины а₀ и a₁ представляют собой две произвольные постоянные, входящие в общее решение дифференциального уравнения второго порядка

(6.4).

Исследование ряда (6.8) показывает, что в общем случае он расходится при z -> ±oо, причем настолько быстро, что волновая функция (6.6) обращается в бесконечность. Нам же нужны всюду ограниченные решения. Они могут быть получены, если ряд (6.8)

оборвать на некотором слагаемом и превратить в полином конечной степени z. Тогда экспоненциальный сомножитель обеспечит затухание функции состояния (6.6) на бесконечности. Такие полиномы также будут решениями уравнения (6.7).

Итак, обрываем ряд на члене с индексом n: а_n /= 0; все старшие коэффициенты, начиная с а_n+2, равны нулю; с помощью формулы (6.12) имеем

λ = 2n+1. (6.13)

Рекуррентная формула принимает вид

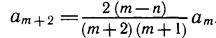
(6.14)

Полиномы с коэффициентами (6.14) обозначаются символом Н_n(z). В них мы можем еще распорядиться по своему усмотрению коэффициентом при низшей степени z. Это будет а₀ или а₁ (если n четно, то в полиноме содержатся только члены с четными степенями z, если n нечетно — с нечетными). Обычно постоянные выбирают так, чтобы коэффициент при высшей степени z был равен 2ⁿ.

Тогда полиномы совпадают с хорошо изученными в математике полиномами Чебышева — Эрмита. Их можно получить с помощью полиномообразующей формулы

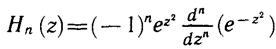
(6.15)

Функции состояния для квантового осциллятора находим:

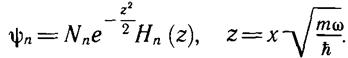
-— I—

yn = Nne 2Hn(z), z = x-Ja&. (6.16)

V я

Нормировочный множитель Л/„ находится из условия

отсюда

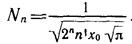
N± (6-17)

Далее с помощью формул (6.15) и (6.17) мы вычислим несколько ψ_n.

Date: 2015-05-19; view: 1128; Нарушение авторских прав