Вероятность обнаружения частицы в момент времени t в элементарном объеме dV около точки с координатами х, у, z определяется формулой

dW=|ψ|²dV. (2.1)

При этом частица представляется в виде точки, в которой сосредоточены ее масса, импульс и энергия.

Из уравнения (2.1) следует

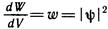. (2.2)

Квадрат модуля волновой функции есть плотность вероятности для местонахождения частицы (поэтому ψ-функцию называют также амплитудой вероятности).

В определениях (2.1) и (2.2) и заключен физический смысл функции состояния, ибо посредством измерений можно найти только величины dW и ω.

Функция состояния ψ(х, у, z, t) является комплексной: квадрат ее модуля выражается формулой

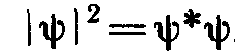
где звездочка обозначает комплексное сопряжение.

Комплексная функция всегда может быть представлена в виде

ψ = R(x, у, z, t)e^ia{x,y,z,t) (2.3)

Здесь

R (х, у, z, t)

— модуль функции, a

e^ia{x,y,z,t)

называется фазовым множителем.

Из формул (2.1) и (2.3) следует, что волновая функция определена неоднозначно, а с точностью до произвольного фазового множителя. Действительно, умножение функции на экспоненту e^iβ изменяет фазу комплексной функции ψ(х, у, z, t), но не ее модуль, что не приводит к изменению измеряемой величины ω.

Указанную особенность функции состояния не следует рассматривать как недостаток теории. Всегда нужно помнить, что волновая функция есть математический объект. Ее даже нельзя найти экспериментально прямым измерением. Непосредственно измеримой характеристикой является величина |ψ|², а она задана однозначно. Произвол в фазовом множителе не приводит ни к каким наблюдаемым эффектам и поэтому является физически несущественным. (Здесь мы говорим только о положении микрочастицы в пространстве.)

В соответствии с определением (2.1) можно по известной ψ-функции рассчитать вероятность обнаружения частицы в любом конечном объеме V. Для этого следует разбить конечный объем на малые элементарные объемы dV, найти для них вероятности dW и по теореме о сложении вероятностей несовместимых событий сложить их:

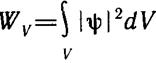. (2.4)

Формула (2.4) вместе с формулой (2.2) лежит в основе реальных измерений вероятности. Однако мы не отметили еще одно необходимое свойство ψ-функции. Если провести интегрирование в формуле (2.4) по всему пространству (или по тому объему, в котором

нахождение частицы — достоверный факт), то интеграл должен быть равен единице, ибо обнаружение частицы здесь есть событие достоверное; вероятность его равна единице:

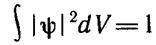. (2.5)

Равенство (2.5) называется условием нормировки функции состояния. Полезно заметить, что в процессе теоретического отыскания ψ-функция часто оказывается ненормированной, т. е. интеграл (2.5) равен не единице, а некоторому числу N. В таком случае легко находится нормированная функция: ψ-функция снабжается необходимым коэффициентом

.

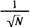Определения (2.1), (2.2), формула (2.4) и условие (2.5) отражают вероятностно-статистический смысл волновой функции. В связи с физическим толкованием возникают ограничения, накладываемые на ψ-функцию: она должна быть однозначной, непрерывной

и квадратично-интегрируемой функцией. Последнее требование означает ограниченность интеграла

,

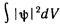взятого по всему пространству: без этого нельзя добиться выполнения равенства B.5). По

этой же причине на ψ-функцию обычно накладывают условие ограниченности: |ψ| < oо. Во многих случаях ограниченность означает,

что

lim |ψ | =0,

причем |ψ| достаточно быстро затухает на бесконечности.

Пример 2.1. Квадратично-интегрируемая функция на конечном промежутке.

Рассмотрим функцию ψ = С sin —, заданную на отрезке @, а) оси Ох. Вычисле-

Вычисления показывают, что

а

\ С sin — dx = -p- С,

J а 2

т. е. это ограниченная величина.

Пример 2.2. Квадратично-интегрируемая функция на бесконечном проме-

Date: 2015-05-19; view: 766; Нарушение авторских прав