Стационарное движение частицы вдоль прямой в поле консервативной силы

Рассмотрим теперь движение частицы вдоль оси х с позиций кванто­вой механики. Согласно представлениям этой теории движение частицы следует описывать посредством волновой функции, которая в данном случае будет зависеть от времени t и только одной координаты х:

ψ = ψ (t,x) (20.18)

Волновая функция может быть найдена из уравнения Шредингера (4.29), которое представляет собой основной закон квантовой механики.

В рассматриваемом случае определяемый формулой (4.23) оператор
полной энергии 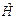, так же, как и волновая функция ψ, будет зависеть
только от координаты х:

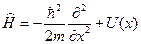. (20.19)

Подстановка этого выражения в уравнение Шредингера (4.29) преобразует его к виду

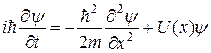(20.20)

Стационарное движение частицы вдоль оси х описывается волновой функцией

, (20.21)

где φ = φ (x) - функция, удовлетворяющая стационарному уравнению Шредингера (4.42), которое теперь будет иметь вид

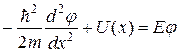(20.22)

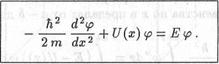
Это есть обыкновенное линейное дифференциальное уравнение, решение которого может быть найдено без труда в тех случаях, когда зависимость U = U(x) потенциальной энергии U от координаты х является достаточ­но простой. Некоторые такие случаи будут рассмотрены в следующих разделах.

Запишем уравнение (20.22) так, как это принято в теории дифферен­циальных уравнений, начиная со старшей производной, а коэффициент при ней сделаем равным единице:

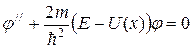(20.23)

При решении этого уравнения необходимо будет использовать некото­рые дополнительные условия, которым должна удовлетворять волновая функция φ = φ (x). Во-первых, по своему физическому смыслу функ­ция φ = φ (x) должна быть непрерывной, т.е. она должна удовлетворять условию

φ (a – 0) = φ (a) = φ (a + 0), (20.24)

где а - произвольное значение координаты х из области определения этой функции. Во-вторых, волновая функция φ = φ (x) должна удовле­творять условию нормировки

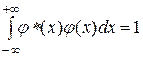
Для этого необходимо, чтобы она была ограниченной, т.е. на бесконеч­ности она должна обращаться в ноль:

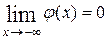
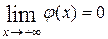
Докажем, что в тех точках на оси х, где потенциальная энергия U = U{x) терпит разрыв, но является ограниченной, первая производная функции φ = φ (x) должна быть непрерывной. С этой целью запишем уравнение (20.22) так:

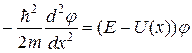
Пусть функция U = U(x) имеет разрыв в точке х = а. Проинтегрируем обе части этого равенства по х в пределах от α – δ до α + δ. Получим

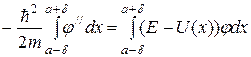
Интеграл в левой части преобразуем по формуле Ньютона - Лейбница:

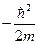(φ ^/ (a + δ) - φ ^/ (a - δ)) =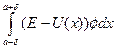

В силу сделанного предположения функция под интегралом в правой части этого равенства ограничена. Поэтому в пределе при δ → 0 этот интеграл будет равен нулю. Таким образом, приходим к условию

φ ^/ (a – 0) = φ ^/ (a + 0). (20.27)

из которого следует, что производная функции φ = φ (x) при х = а не­
прерывна или имеет устранимый разрыв.

Date: 2015-05-19; view: 553; Нарушение авторских прав