Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Стационарные состояния
|
|
Стационарное состояние частицы описывается волновой функцией вида (19.26). Подставим эту функцию в уравнение Шредингера (19.29) и найдем таким образом уравнение для функции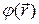 
. Частная производная от функции
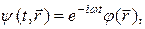
по времени t будет
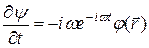
Подстановка этой функции и ее производной в (19.29) приводит к уравнению
(19.42)
где E = ћω.
Уравнение (19.42) называют уравнением Шредингера для стационарных состояний, или просто стационарным уравнением Шредингера. Уравнение (19.42) есть уравнение для собственных функций оператора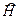 
полной энергии. Поэтому энергия частицы, состояние которой описывается волновой функцией φ, являющейся решением этого уравнения, будет в точности равна соответствующему собственному значению Е гамильтониана Н Н.
С учетом формулы (19.24) уравнение (19.42) можно записать более подробно следующим образом:
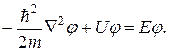(19.43)
Уравнения (19.42) и (19.43) имеют решения не для любых значений энергии Е. Все собственные значения оператора Н полной энергии, для которых эти уравнения имеют решение, образуют так называемый энергетический спектр, или спектр возможных значений энергии частицы. В некоторых случаях эти значения образуют счетное множество, т.е. их можно перенумеровать. Пусть п - номер произвольного собственного значения энергии. При этом энергию частицы можно рассматривать как функцию от номера п: Еп = Е(п). Такой спектр энергий называется дискретным. Каждое значение энергии дискретного спектра можно отметить на числовой оси Е посредством отрезка прямой линии, который называют уровнем энергии (рис. 19.2). Среди возможных значений энергии частицы всегда есть наименьшее. Волновая функция, соответствующая наименьшему значению энергии, описывает так называемое основное состояние частицы.
Иногда различным состояниям частицы соответствует одно и то же значение энергии Е. Такие состояния называют вырожденными. Число g различных стационарных состояний частицы с одной и той же энергией Е называют кратностью вырождения данного значения (уровня) энергии
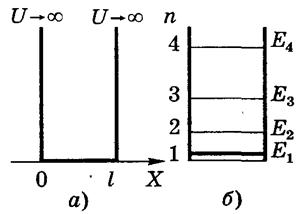
Рис. 19.2. Уровни энергии
Date: 2015-05-19; view: 554; Нарушение авторских прав