Соотношение неопределенностей. Рассмотрим ансамбль частиц, каждая из которых находится в од­ном и том же квантовом состоянии

Рассмотрим ансамбль частиц, каждая из которых находится в од­ном и том же квантовом состоянии. Пусть известна волновая функ­ция 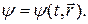описывающая это состояние. Представим себе, что пе­ред физиком-экспериментатором поставлена задача измерить величину а, характеризующую положение в пространстве или движение одной ча­стицы. Предположим, что ему удалось измерить в некоторый момент времени t значения величины а для всех частиц ансамбля. Таким обра­зом экспериментатор получил в свое распоряжение совокупность чисел a _1, a _{2, …,} a_N, где N - число частиц в ансамбле. Результатом измерения величины а является ее среднее значение а, которое экспериментатор найдет по формуле(19.35)

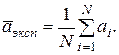
Разность 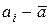называется отклонением значения а 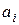от среднего зна­чения 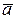, а выражение

=

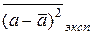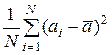
- средним значением квадрата отклонения. Ошибкой измерения величи­ны а, или ее неопределенностью называется величина

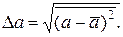(19.37)

Эта величина характеризует "разброс" значений 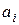в окрестности средне­го значения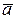

а и определяет точность измерения величины а. Чем меньше 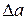, тем выше точность измерения, т.е. с тем большей вероятностью ве­личина, а принимает значение, близкое к 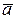. Если 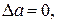то это значит, что величина а в точности равна .

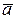Среднее значение 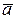и неопределенность 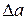величины а для частицы, находящейся в состоянии, описываемом известной волновой функцией 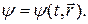, могут быть вычислены теоретически. Для расчета среднего значения в квантовой механике имеется формула (19.25). Среднее зна­чение квадрата отклонения можно вычислить по аналогичной формуле

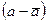² = 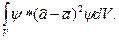(19.38)

В том случае, когда экспериментальные и теоретические значения 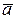и 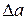совпадают, можно говорить о согласии теории с результатами экспе­риментов.

Квантовая механика описывает движения микрочастиц вещества с учетом их волновых свойств. Это описание осуществляется посредством волновой функции ψ. Необходимость создания квантовой механики была вызвана тем, что движения микрочастиц вещества обладают такими осо­бенностями, которые не могут найти объяснения в рамках классической механики. Одна из таких особенностей движения микрочастиц заклю­чается в следующем. Пусть перед экспериментатором была поставлена задача измерить одновременно координату х и импульс р_х некоторой ми­крочастицы. Точность измерения координаты определяется величиной 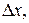, а точность измерения импульса - величиной 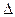р_х, которые можно вычислить по приведенным выше формулам. Оказывается, неопреде­ленност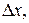и и 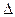р_х всегда удовлетворяют неравенству

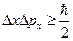(19.39)

В 1927 г. это неравенство было доказано теоретически немецким фи­зиком В.Гейзенбергом и названо соотношением неопределенностей. Со­гласно этому неравенству неопределенности координаты 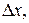и импульса 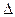р_х не могут быть сколь угодно малы одновременно. Это означает, что координата х и импульс р_х частицы в одном и том же измерении не могут быть определены сколь угодно точно, какими бы совершенными ни были измерительные приборы. Соотношение неопределенностей есть следствие физической природы микрочастиц вещества. Многочисленные измерения подтверждают его справедливость.

19.6. Собственные функции и собственные значения операторов *

Функция 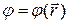называется собственной функцией оператора 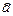, если она является решением уравнения

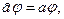(19.40)

где число а называется собственным значением оператора 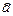. Это урав­нение в общем случае имеет не одно, а множество различных решений. Совокупность всех значений числа а, при которых уравнение (19.40) име­ет решение, называют спектром собственных значений оператор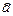а а.

Собственные функции какого-либо оператора а обладают замечательной особенностью. Когда частица находится в состоянии, описываемом
собственной функцией φ оператора 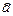а, физическая величина а принимает значение, в точности равное соответствующему собственному зна­чению а, т.е.

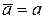и .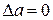

В самом деле, с учетом равенства (19.40) и условия нормировки (19.28) будем иметь

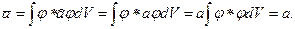
Докажем теперь, что Δ a = 0. Но прежде выведем формулу

(19.41)

согласно которой среднее значение квадрата отклонения равно разности среднего квадрата величины а и квадрата ее среднего значения. Поло­жим в формуле (19.38) ψ= φ и преобразуем ее следующим образом:

=

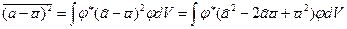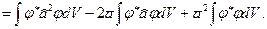
Так как

,

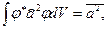
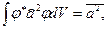
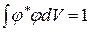после простых преобразований приходим к формуле (19.41).

Вычислим 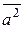при условии, что φ есть собственная функция оператора

=

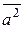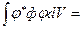
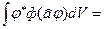
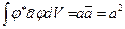
Таким образом, приходим к выводу, что согласно формуле (19.41)

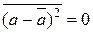и ∆а = 0.

Итак, доказано, что среднее значение 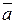в точности равно собственному значению а, которое соответствует данной Собственной функции φ опе­ратора .

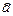Date: 2015-05-19; view: 609; Нарушение авторских прав