Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Падение частицы на потенциальный барьер

⇐ ПредыдущаяСтр 24 из 95Следующая ⇒




 

Рассмотрим движение частицы вдоль оси х в консервативном силовом поле, описываемом следующей зависимостью потенциальной энергии U от координаты х:

 

 

0 при x 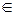(- ∞, 0),

U (x) = 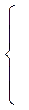U 0 при x 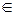(0, + ∞),

 

 

U0 U = U (x) x = 0, + ∞

E < U0 x < ∞ при х 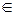(- ∞, 0), Uo при х 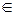(0, + ∞), (20.43)

 

где Uо ~ положительная постоянная, называемая "высотой" потенци­ального барьера. График зависимости (20.43) приведен на рис. 20.7. Эту зависимость следует рассматривать как идеализацию зависимости U = U(x), график которой изображен на рис. 20.2. Производная функ­ции (20.43) всюду на оси х, за исключением точки х = 0, равна нулю. В точке х = 0 производная этой функции равна + ∞. Из этого следует, что при движении частицы вдоль оси х только на узком интервале в окрест­ности точки х = 0 на нее будет действовать сила, которая направлена в сторону, противоположную оси х.

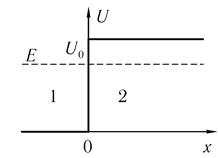
Рис. 20.7. Потенциальный барьер

Пусть на потенциальный барьер падает однородный поток частиц, дви­жущихся слева направо.

случай Е < Uо

Рассмотрим случай, когда энергия Е каждой из падающих на барьер частиц меньше высоты Uo барьера:

Е < Uо.

В области перед барьером, где х < 0, потенциальная энергия частицы

равна нулю и уравнение (20.23) можно записать так:

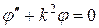при x < 0.

 

Здесь

.

 

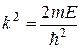Общее решение уравнения (20.44) имеет вид

 

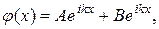при х < 0.

где А и В - постоянные интегрирования. Таким образом, в области, где х < 0, волновая функция ψ = ψ (t,x) будет представлять собой сумму (20.7) двух волн, одна из которых

ψ+ (t, x) бежит направо, т.е. падает на барьер, а другая ψ- (t, x) - налево, т.е. отражается от барьера.

В области, где х > 0, потенциальная энергия U равна Uo. Для этих значений х уравнение (20.23) можно привести к виду

 

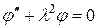при x > 0. (20.47)

 

Здесь

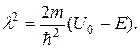(20.48)

 

 

Общее решение уравнения (20.47) имеет вид

 

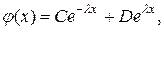
где С и D - постоянные. Коэффициент D следует положить равным нулю, так как в противном случае функция φ (x) будет неограниченно возрастать при x → ∞, что лишено физического смысла. Итак, волновая функция

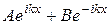при x < 0,

φ (x) = Ce-λx при x > 0. (20.49)

 

Эта функция и ее производная непрерывны всюду, кроме точки х = 0, в которой они также должны быть непрерывны:

 

 

φ (-0) = φ (+0),

 

φ/ (-0) = φ/ (+0). (20.50)

 

 

Подстановка выражений (20.49) в эти условия приводит к системе урав­нений

 

A + B = C,

ik (A – B) = - λC.

р азрешив которые относительно В и С, получим формулы

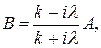
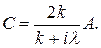
Теперь функцию (20.49) можно записать так:

 

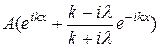при x ≤ 0,

φ (x) =

при x > 0.

 

 

При помощи формулы Эйлера

 

eia = cos α + sin α

 

функцию φ (x) при x < 0 нетрудно преобразовать к виду

φ (x) = 2 Ae-iβ cos (kx + β),

 

где п

β = arctg .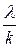

 

Используя полученные выражения для функции φ (x), построим график зависимости от координаты х концентрации частиц в потоках, падающих на потенциальный барьер, отраженных от него и преодолевших его:

n (x) = | φ (x)|2.

График этой зависимости показан на рис. 20.8.

 

n = | φ|2

 

0 х

Рис. 20.8. Интерференция волновых функций и туннельный эффект

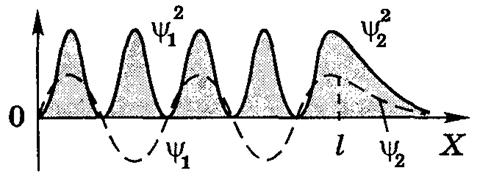
'Зависимость n = n (x) на рис. 20.8 демонстрирует существенное раз­личие в движениях потоков частиц по законам классической механики и по законам механики квантовой. Согласно законам классической меха­ники концентрации частиц, падающих и отраженных от потенциального барьера в области х < 0 всюду одинаковы; а в области x > 0 концентра­ция частиц должна быть равна нулю при условии, что энергия частицы Е меньше высоты Uo потенциального барьера. Как видно из графика на рис. 20.8, вследствие интерференции волн ψ+ (t, x) и ψ- (t, x), падающей на барьер и отраженной им, концентрация частиц в области х < 0 пери­одически изменяется. Волновые свойства частиц проявляются также в том, что их концентрация в области

х > 0 не равна нулю. Эти свойства микрочастиц позволяют им проникать в те области пространства, где их присутствие запрещено законами классической механики. Это явление называют туннельным эффектом.

В области за барьером волновая функция ψ имеет вид.

ψ (t,x) = Ce-iωt-λx

Эта функция - не бегущая волна. Она описывает неподвижное "облако" частиц, средняя скорость которых равна нулю.

В области х > 0 концентрация частиц убывает по закону

n (x) = n (0) e-2λx

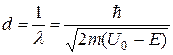
Согласно этой формуле на расстоянии d = λ- 1 от барьера, т.е. места, где на частицы действует тормозящая их движение сила, концентрация частиц имеет значение

 

n (d) = n (0) e- 2 ≈ 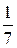n (0).

называют глубиной проникновения частиц за барьер. Из этой формулы видно, что глубина d тем больше, чем меньше разность Uo - Е. Когда энергия частицы будет больше или равна высоте барьера, глубина про­никновения d станет бесконечно большой.

Интересно рассмотреть предельный случай, когда высота барьера Uo стремится к бесконечности. При этом будет неограниченно возрастать сила, которая тормозит движение частиц в окрестности точки х = 0. Очевидно, что в предельном случае бесконечно высокого барьера части­цы не смогут его преодолеть и их концентрация за барьером будет равна

нулю. В самом деле, при Uo → ∞ величина λ, определяемая формулой (20.48), также стремится к бесконечности. При этом предельная волно­вая функция будет

 
 


A (eikx – e-ikx) = 2 i A sin kx при x < 0

φ (x) =

0 при x > 0

 

Случай E>U0.

Рассмотрим теперь падение на барьер потока частиц, которые летят из - ∞ и энергия Е каждой из которых больше высоты барьера Uo

E>U0.

В этом случае уравнение (20.23) при х > 0 следует записать так:

φ// + 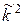φ = 0 при x > 0. (20.51)

Здесь

 

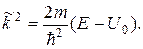(20.52)

Общее решение уравнения(20.23) имеет вид:

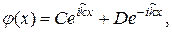
Где С и D - постоянные интегрирования. Первое слагаемое в этой сумме описывает волну, бегущую направо от барьера, а второе - волну, бегущую в противоположную сторону из + оо. По смыслу рассматриваемой задачи в области за барьером, где х > 0, может существовать только первая волна, описывающая поток частиц, преодолевших действие тормозящей силы. Поэтому коэффициент D следует положить равным нулю. Итак, в случае, когда Е > Uo, волновая функция будет

 

 
 


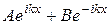при x < 0,

φ (x) = 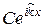при x > 0. (20.53)

 

 

Условия (20.50) непрерывности функции <р(х) и ее производной приводят
к уравнениям

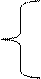
A + B = C,

ik (A – B) = ,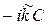

 

Из этих уравнений найдем амплитуды отраженной от барьера и прошед­шей за него волн:

 

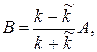
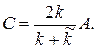
Произведение концентрации п частиц в потоке на их скорость v есть число частиц, пересекающих за единицу времени единичную площадку, перпендикулярную к траекториям частиц. Очевидно, что произведение п v для потока частиц, падающих на барьер, равно сумме таких произве­дений для потоков отраженных от барьера частиц и частиц, прошедших за барьер:

(nv) naд = (nv) omp + (nv) npoш.

Концентрация частиц в однородных потоках равна квадрату амплиту­ды волны, а скорость частицы связана с импульсом и волновым числом

Соотношениями

 

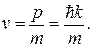
Таким образом, приходим к равенству

| A |2 k = | B |2 k + | C |2 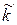, (20.55)

которое выражает закон сохранения числа частиц.

Отношение квадратов модулей амплитуд отраженной и падающей волн

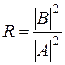(20.56)

есть доля частиц, отраженных от барьера, или вероятность отражения от него одной из падающих частиц. Величину R называют коэффициен­том отражения. С учетом формул (20.54) его можно выразить через волновые числа k и :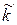

 

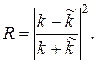
Отметим, что в случае, когда Е < Uo, коэффициент отражения равен единице:

 

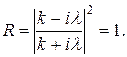
Отношение

 

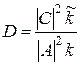
есть доля частиц, прошедших за барьер, или вероятность проникновения за барьер одной из падающих на него частиц. Это отношение называют коэффициентом прохождения. В силу закона сохранения числа частиц (20.55) коэффициенты R и D связаны соотношением

 

R + D = 1.

При Е > Uо с учетом формул (20.54) будем иметь

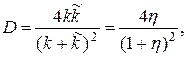
где параметр

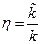
т.е. отношение волновых чисел, при помощи формул (20.45) и (20.52) можно представить как функцию от энергии частицы:

 

 

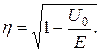
Нетрудно видеть, при изменении энергии частицы Е от значения Uo до + ∞ параметр η монотонно возрастает от нуля до единицы. При этом коэффициент прохождения D также монотонно возрастает от нуля до единицы.

В случае, когда энергия Е падающей на потенциальный барьер части­цы больше его высоты Uo, классическая и квантовая теории также пред­сказывают различное поведение частиц после действия на них тормозя­щей силы. Согласно законам классической механики частица с энергией Е > Uо преодолевает участок пути, где на нее действует тормозящая ее движение сила, и летит дальше. Поэтому все частицы в потоке, па­дающем на барьер, должны были бы пройти через него и удалиться на бесконечность. Однако так не происходит. Квантовая механика предска­зывает, что часть R падающих на барьер частиц будет отброшена назад, как бы велика ни была энергия частицы Е. Этот эффект(20.57)

также есть проявление волновых свойств частиц.

Некоторые выводы классической и квантовой теорий совпадают. Рас­смотрим один из таких выводов. Импульсы р и 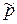частицы до и после прохождения барьера связаны с волновыми числами соотношениями де Бройля:

p = ħk, p = ħ .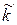

 

 

При помощи формул (20.45) и (20.52) получим равенство

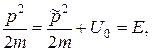U = U (x)

 

которое выражает собой закон сохранения энергии.

Рассмотрим теперь движение частиц в силовом поле, которое харак­теризуется зависимостью U = U(х) потенциальной энергии частицы от координаты х, изображенной графически на рис. 20.9.

 

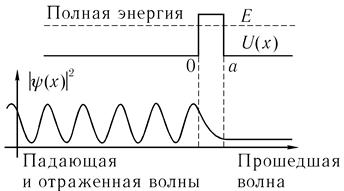
Рис. 20.9. Потенциальный барьер прямоугольной формы

Такая зависи­мость означает, что в окрестности точки х = 0 на частицу действует сила, направленная против оси х, а в окрестности точки x = l - сила, направленная в ту же сторону, что ось х.

Пусть энергия частиц Е меньше высоты Uo потенциального барьера: Е < U0. В этом случае волновая функция φ = φ (x) слева и справа от барьера, т.е. при x 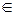(-∞, 0) U(l, +∞), будет удовлетворять уравне­нию (20.44); а внутри барьера, т.е. при x 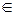(0, l), - уравнению (20.47). Если поток частиц падает на барьер слева направо, то волновая функция должна иметь вид

 

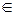Aeikx + Be-ikx при x (- ∞, 0),

φ (x) = aeλx + be-λx при x 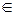(0, l),

 

Ceikx при x 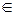(l, + ∞).

 

 

Эта функция должна удовлетворять граничным условиям

 

 

φ (- 0) = φ (+ 0),

φ/ (- 0) = φ/ (+ 0),

φ (l - 0) = φ (l + 0),

φ/ (l – 0) = φ/ (l + 0).

 

согласно которым волновая функция и ее производная должны быть непрерывны в точках x = 0 и x = l. Эти условия приводят к равенствам

 

A + B = a + b,

ik (A – B) = λ (a – b),

aeλl + be-λl = Ceikl,

λ (aeλl – be-λl) = ikCeikl.

 

 

Умножим первое уравнение на ik и сложим со вторым, третье также умножим на ik и вычтем из него четвертое. Придем к системе уравнений

λ + ik) a – (λ – ik) b = 2 ikA,

(λ – ik) aeλl – (λ + ik) be-λl = 0,

которыеразрешим относительно а и b:

а = 2i(j.+ i)fAe-xl,

b = 2i(j-i)fAexl,

где

,

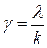f = ((γ + i)2 e-λl – (γ – i)2 eλl).

В силу неравенства

 

eλl > e-λl

справедливо приближенное равенство

 

 

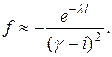
Теперь нетрудно выразить амплитуду С волны, прошедшей за барьер, через амплитуду А волны, падающей на него:

C = (aeλl + be-λl) e-ikl = 4 iγfAe-ikl ≈ -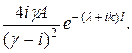

Найдем по формуле (20.57) коэффициент прохождения D. Так как волновое число 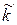волны, прошедшей за барьер, равно волновому числу k, будем иметь

 

 

 

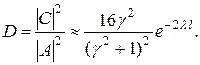
С учетом обозначения (20.48) этой формуле можно придать вид

 

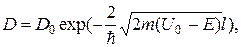
где

 

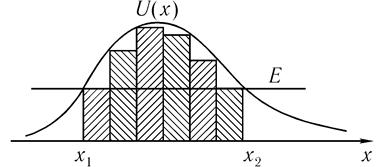
Рис. 20.10. Потенциальный барьер произвольной формы

Коэффициент D прохождения частицы через потенциальный барьер произвольной формы (рис. 20.10) можно вычислить по формуле

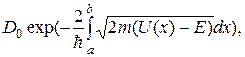
где а и b - значения координаты х, при которых функция U(x) равна Е. "Туннельный эффект", т.е. явление прохождения частиц через потен­циальный барьер, высота которого Uo больше энергии частицы Е, было обнаружено экспериментально.

 
⇐ Предыдущая19202122232425262728Следующая ⇒

Date: 2015-05-19; view: 1046; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию